Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Three Dimensional Coordinates Solutions Exercise 5(a) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Three Dimensional Coordinates Solutions Exercise 5(a)
I.
Question 1.
Find the distance of P (3, -2,4) from the origin.
Solution:
OP = \(\sqrt{x^{2}+y^{2}+z^{2}}=\sqrt{9+4+16}\)
= √29 units
Question 2.
Find the distance between the points (3,4,¬2) are (1,0,7).
Solution:

II.
Question 1.
Find x if the distance between (5, -1,7) and (x, 5,1) is 9 units.
Solution:
P(5, -1, 7), Q(x, 5,1) are the given points
PQ = 9
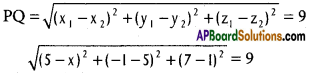
(5 – x)² + 36 + 36 = 81
(5 -x)² = 81 – 72 = 9
5 – x = ± 3
5 – x = 3 or 5 – x = -3
x = 5 – 3 or x = 5 + 3
= 2 or 8
![]()
Question 2.
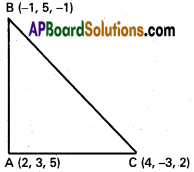
Show that the points (2,3,5), (-1,5, -1) and (4, -3, 2) form a right angled iso-sceles triangle.
Solution:
A(2, 3, 5) B(-1, 5, -1), C(4, -3, 2) are the given points
AB² = (2 + 1)² + (3 – 5)² + (5 + 1)²
= 9 + 4 + 36 = 49
BC² = (-1- 4)² + (5 + 3)² + (-1 – 2)²
= 25 + 64 + 9 = 98
CA² = (4 – 2)² + (-3 -3)² + (2 – 5)²
= 4 + 36 + 9 = 49
AB² = CA² ⇒ AB² + CA² = 49 + 49 = 98 = BC²
ABC is a right angled isosceles triangle.
Question 3.
Show that the points (1, 2, 3), (2, 3, 1) and (3, 1, 2) form an equilateral triangle.
Solution:
A( 1, 2, 3), B(2, 3, 1) and C (3, 1, 2) are the given points
AB² = (1 – 2)² + (2 – 3)²+ (3 – 1)²
= 1 + 1+ 4 = 6
BC² = (2 – 3)² + (3 – 1)² + (1 – 2)²
= 1 + 4 + 1 = 6
CA² = (3 – 1)² + (1 – 2)² + (2 – 3)²
= 4 + 1 + 6
AB² = BC² = CA² ⇒ AB = BC = CA
∴ ABC is an equilateral triangle
![]()
Question 4.
P is a variable point which moves such that 3PA = 2PB. If A = (-2, 2,3) and B = (13, -3,13) prove that P satisfies the equation.
x² + y² + z² + 28x – 12y + 10z – 247 = 0.
Solution:
A(-2, 2, 3) and B(13, -3, 13) are the given points. P(x, y, z) is any point on the locus.
Given condition is 3P A = 2P B
⇒ 9 PA² = 4PA²
9[(x + 2)² + (y – 2)² + (z – 3)²] = 4[(x – 13)²+(y + 3)² + (z – 13)²]
⇒ 9(x² + 4x +4 + y² – 4y + 4 + z² – 6z + 9) = 4(x² – 26x + 169 + y² + 6y + 9 + z² – 26z + 169)
⇒ 9x² + 9y² + 9z² + 36x – 36y – 54z +153 = 4x² + 4y² + 4z² – 104x + 24y – 104z + 1388
5x² + 5f + 5z² + 140x – 60y + 50z – 1235 =0
Dividing with 5 locus of P is
x² + y² + z² + 28x – 12y + 10z – 247 = 0
Question 5.
Show that the points (1, 2, 3) (7, 0, 1) and (-2, 3, 4) are collinear.
Solution:
A (1, 2, 3), B(7, 0, 1) C(-2, 3, 4) are the given points.

AB + AC = 2√11 + √11 = 3√11 = BC
A, B, C are collinear
![]()
Question 6.
Show that ABCD is a square where A, B, C, D are the points (0, 4, 1), (2, 3 -1) (4, 5, 0) and (2, 6, 2) respectively.
Solution:
A(0, 4, 1), B(2, 3, -1) C(4, 5, 0), D(2, 6, 2) are the given points.
AB² = (0 – 2)² + (4 – 3)² + (1 + 1)²
=4 + 1 + 4 = 9
BC² = (2 – 4)² + (3 – 5)² + (-1 – 0)²
= 4 + 4 + 1 = 9
CD² = (4- 2) ²+ (5 – 6)² + (0 – 2)²
= 4 + 1 – 4 = 9
DA² = (2- 0) ²+ (6 – 4)² + (2 – 1)²
= 4 + 4 + 1 = 9
AB² = BC² = CD² = DA²
⇒ AB = BC = CD = DA
AC² = (0 – 4)² + (4 – 5)² + (1 – 0)² = 16 + 1 + 1 = 18
BD² = (2 – 2)² + (3 – 6)² + (-1 -2)² = 9 + 9 = 18
AC² = BD² ⇒ AC = BD
AB² + BC² = 9 + 9 = 18 = AC²
⇒ ∠ABC = 90°
A, B, C, D are the vertices of a square.