Inter 1st Year Maths 1B The Straight Line Solutions Ex 3(e)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B The Straight Line Solutions Exercise 3(e) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B The Straight Line Solutions Exercise 3(e)

I.

Question 1.
Find the incentre of the triangle whose vertices are (1, √3) (2, 0) and (0, 0)
Solution:
0(0, 0), A (1, √3), B (2, 0) are the vertices of ∆ ABC

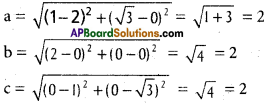
∴ ABC is an equilateral triangle
Co-ordinates of the in centre are

Question 2.
Find the orthocentre of the triangle whose sides are given by x + y + 10 = 0, x – y – 2 = 0 and 2x + y – 7 = 0
Solution:
Equation of AB is x + y + 10 = 0 ………… (1)
Equation of BC is x – y – 2 = 0 ………… (2)
Equation of AC is 2x + y – 7 = 0 ………… (3)

Solving (1) and (2) co – ordinates of B are (-4, -6)
Solving (1) and (3) co – ordinates of A are (17, -27)
Equation of BC is x – y – 2 = 0
AD is perpendicular to BC.
Equation of AD is x + y + k = 0
AD passes through A (17, -27)
17 – 27 + k = 0 ⇒ k = 10
∴ Equation of AB is x + y + 10 = 0 ………….. (1)
Equation of AC is 2x + y – 7 = 0
BE is perpendicular to AC.
Equation of DE can be taken as x – 2y = k
BE passes through D (-4, -6)
-4 + 12 = k ⇒ k = 8
Equation of BE is x – 2y = 8

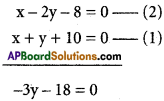
3y = -18 ⇒ y = – 6 x + y+10 = 0
⇒ x – 6+10 = 0
x = 6 – 10 = -4
Orthocentre of A ABC is (- 4, – 6)

Question 3.
Find the orthocentre of the triangle whose sides are given by 4x – 7y + 10 = 0, x + y = 5 and 7x + 4y = 15
Solution:
Equation of AB is. 4x – 7y + 10 = 0 …………. (1)
Equation of BC is x + y = 5 …………. (2)
Equation of AC is 7x + 4y – 15 = 0 …………. (3)
AB and AC are perpendicular and ∠A = 90°
∴ ABC is a right angled triangle
Right angled vertex A is the orthocentre
Solving (1) and (3)

Orthocentre is O (1,2)

Question 4.
Find the circumcentre of the triangle whose sides are x = 1, y = 1 and x + y = 1
Solution:
Equation of AB is x = 1
Equation of BC is y = 1
Equation of AC is x + y = 1

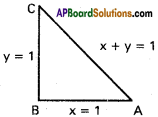
AB and BC are perpendicular
∴ ABC is a right angled triangle and ∠B = 90°
Mid point of AC is the circumcentre
Co-ordinates of A are (1,0) and C are (0,1)
Circumcentre is (\(\frac{1}{2}\), \(\frac{1}{2}\))

Question 5.
Find the incentre of the triangle formed by the lines x = 1, y = 1 and x + y = 1
Solution:
Equation of AB is x = 1
Equation of BC is y = 1
Equation of AC is x + y = 1
Solving the vertices are A(1, 0), B(1, 1), C (0, 1)

Question 6.
Find the circumcentre of the triangle whose vertices are (1,0),(-l, 2) and (3,2)
Solution:
A (1, 0), B (-1, 2), C (3, 2) are the vertices of ∆ ABC

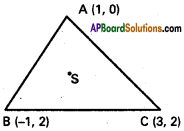
S (x, y) is the circumcentre of ∆ ABC
SA = SB = SC
SA = SB ⇒ SA² = SB²
(x – 1)² + y² = (x + 1)² + (y – 2)²
x² – 2x + 1 + y² = x² + 2x + 1 + y² – 4y + 4
4x – 4y = – 4 ⇒ x – y = -1 …….. (1)
SB = SC ⇒ SB² = SC²
(x+ 1)² + (y – 2)² = (x-3)² + (y – 2)²
x² + 2x + 1 = x² – 6x + 9
8x = 8 ⇒ x = 1
From (1), 1 – y = -1
y = 2
∴ Circumcentre is (1, 2)

Question 7.
Find the value of k, if the angle between the straight lines kx + y + 9 =0 and 3x – y + 4 = 0 is π/4
Solution:
Equations of the given lines are
kx + y + 9 = 0
3x – y + 4 = 0

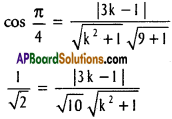
Squaring and cross-multiplying
5k² + 5 = (3k – 1)² = 9k² – 6k + 1
4k² – 6k – 4 = 0
2k² – 3 k – 2 = 0
(k – 2) (2k + 1) =0
k = 2 or -1/2

Question 8.
Find the equation of the straight line passing through the origin and also through the point of intersection of the lines 2x – y + 5 = 0 and x + y + 1 = 0.

Solution:
Equation of AB is L₁ = 2x – y + 5 = 0
Equation of AC is L₂ = x + y+ l = 0
Equation of any line passing through A is
L₁ + kL₂ = 0
(2x – y + 5) +k (x + y + 1) = 0 ……….. (1)
This line passes through O (0, 0)
5 + k = 0 ⇒ k = -5
Substituting in (1), equation of OA is
(2x – y + 5) – 5(x + y + 1) =0
2x – y + 5 – 5x – 5y – 5 = 0
-3x- 6y = 0 ⇒ x + 2y = 0

Question 9.
Find the equation of the straight line parallel to the line 3x + 4y = 7 and passing through the point of intersection of the lines x – 2y – 3 = 0 and x + 3y – 6 = 0.
Solution:
Equation of the given lines are
L₁ = x – 2y – 3 = 0 and
L₂ = x + 3y – 6 = 0
Equation of any line passing through the intersection is L₁ + kL₂ = 0
(x – 2y – 3) + k(x + 3y – 6) = 0
(1 + k)x + (-2 + 3k)y + (-3 – 6k) = 0
This line is parallel to 3x + 4y = 7
a₁b₂ = a₂b₁
3(-2 + 3k) = (1+ k) 4
-6 + 9k = 4 + 4k ⇒ 5k=10 ⇒ k = 2
Equation of the required line is 3x + 4y – 15 = 0

Question 10.
Find the equation of the straight line perpendicular to the line 2x + 3y = 0 and passing through the point of intersection of the lines x + 3y – 1 = 0 and x – 2y + 4 = 0.
Solution:
Equation of AB is x + 3y – 1 = 0
Equation of AC is x – 2y + 4 = 0

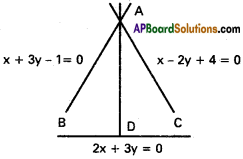
Equation of any line through A is
(x + 3y – 1) + k(x – 2y + 4) = 0
(1 + k)x + (3 – 2k)y + (4k – 1) = 0 ………… (1)
This line is perpendicular to 2x + 3y = 0
a₁a₂ + b₁b₂ = 0
2(1 +k) + 3(3 – 2k) = 0
2 + 2k + 9 – 6k = 0
4k = 11 ⇒ k = \(\frac{11}{4}\)
Substituting in (1), equation of the required line AD is
(1 + \(\frac{11}{4}\))x + (3 – \(\frac{11}{2}\))y + (11 – 1) = 0
\(\frac{15}{4}\) x – \(\frac{5}{2}\)y + 10 = 0
15x – 10y + 40 = 0
3x – 2y + 8 = 0

Question 11.
Find the equation of the straight line making non-zero equal intercepts on the coordinate axes and passing through the point of intersection of the lines 2x – 5y + 1 = 0 and x – 3y – 4 = 0.
Solution:
Equation of the given lines are
L₁ = 2x – 5y + 1 = 0
L₂ = x – 3y – 4 = 0
Equation of any line passing through the intersection of these lines is L₁ + kL2 = 0
(2x – 5y + 1) + k(x – 3y – 4) = 0
(2 + k)x – (5 + 3k)y + (1 – 4k) = 0 …………. (1)
Intercepts on co-ordinate axes are equal
2 + k = -5 – 3k
4k = – 7 ⇒ k = -7/4
Substituting in (1)
Equation of the required line is
(2 – \(\frac{7}{4}\))x – (s – \(\frac{21}{4}\))y+ (1 + 7) = 0
\(\frac{1}{4}\) x + \(\frac{1}{4}\)y + 8 = 0
⇒ x + y + 32 = 0

Question 12.
Find the length of the perpendicular drawn from the point of intersection of the lines 3x + 2y + 4 = 0 and 2x + 5y – 1 = 0 to the straight line 7x + 24y -15 = 0.
Solution:
Equation of the given lines
3x + 2y + 4 = 0
2x + 5y – 1 = 0

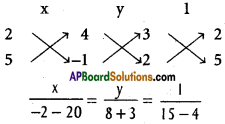
x = \(\frac{-22}{11}\) = -2, y = \(\frac{11}{11}\) = 1
Co-ordinates of P are (-2, 1)
Equation of the line is 7x + 24y- 15 = 0
Length of the perpendicular

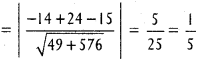
Question 13.
Find the value of ‘a’ if the distances of the points (2, 3) and (-4, a) from the straight line 3x + 4y – 8 = 0 are equal.
Solution:
Equation of P’Q’ is 3x + 4y – 8 = 0 P (2, 3), Q (- 4, a) are the given points
PP’ and QQ’ are the perpendicular from P and Q.

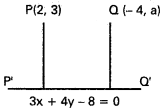
PP’ = QQ’
\(\frac{|3.2+4.3-8|}{\sqrt{9+16}}=\frac{|3 .(-4)+4 a-8|}{\sqrt{9+16}}\)
10 = |4a – 20|
4a – 20 = ±10 ⇒ 4a = 20 ± 10 = 30 or 10
a = \(\frac{30}{4}\) or \(\frac{10}{4}\)
i.e., a = \(\frac{15}{2}\) oe \(\frac{5}{2}\)

Question 14.
Find the circumcentre of the triangle formed by the straight lines x + y = 0, 2x + y + 5 = 0 and x – y = 2.
Solution:
Equation of AB is x + y = 0 ………….. (1)
Equation of BC is 2x + y + 5 = 0 ………….. (2)
Equation of AC is x – y = 2 ………….. (3)

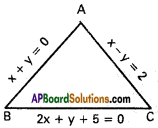
Solving (1) and (2) co-ordinates of D are (-5, 5)
Solving (2) and (3) co-ordinates of C are (-1, -3)
Solving (1) and (3) co-ordinates of A are (1, -1)
Suppose S(x, y) is the circumcentre
SA = SB = SC
SA = SB ⇒ SA² = SB²
(x + 5)² + (y – 5)² = (x + 1)² + (y + 3)²
x² + 10x + 25 + y² – 10y + 25
= x² + 2x + 1 + y² + 6y + 9
8x – 16y = -40
x – 2y = -5 ………… (1)
SB = SC ⇒ SB² = SC²
(x+ 1)² + (y + 3)² = (x -1)² + (y + 1)²
x² + 2x + 1 + y² + 6y+9
= x² – 2x + 1 + y² + 2y + 1
4x + 4y = -8
x + y = -2 …………… (2)
(2) – (1) gives 3y = 3 ⇒ y = 1
x + 1 = -2 ⇒ x = -3
Circumcentre is S(-3, 1)

Question 15.
If 6 is the angle between the lines \(\frac{x}{a}+\frac{y}{b}=1\) and \(\frac{x}{b}+\frac{y}{a}=1\) , find the value of sin 0 when a > b.
Solution:
Equation of AB is. \(\frac{x}{a}+\frac{y}{b}=1\) ⇒ bx + ay = ab
Equation of AC is. \(\frac{x}{b}+\frac{y}{a}=1\) ⇒ ax + by = ab

II.

Question 1.
Find the equation of the straight lines passing through the point (-10, 4) and making an angle 0 with the line x – 2y = 10 such that tan θ = 2.
Solution:
Equation of QR is x – 2y = 10

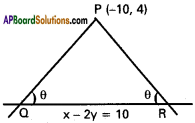
Suppose slope of PQ is m, PQ passes through P(-10, 4)
Equation Of PQ is y – 4 = m(x + 10)
= mx + 10m
i.e., mx-y + (10m + 4) = 0 …………… (1)
tan θ = 2 ⇒ cos θ = \(\frac{1}{\sqrt{5}}\)

Squaring and cross multiplying
m² + 1 = (m + 2)²
= m² + 4m + 4
4m + 3 = 0
m = –\(\frac{3}{4}\)

Case (i) : Co-efficient of m² = 0
⇒ One of the roots is ∞
Hence PR is a vertical line
∴ Equation of PR is x + 10 = 0

Case (ii): m = –\(\frac{3}{4}\)
Substituting in (1)
Equation of PQ is – \(\frac{3}{4}\)x – y + (\(\frac{30}{4}\) + 4) = 0
\(\frac{-3 x-4 y-14}{4}=0\)
⇒ 3x + 4y + 14 = 0

Question 2.
Find the equation of the straight lines pass-ing through the point (1, 2) and making an angle of 60° with the line √3x + y + 2 = 0.
Solution:
Equation of QR is √3x + y + 2 = 0

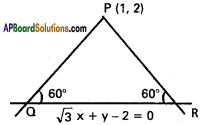
PQ and PR passes through P( 1, 2) and makes an angle of 60° with QR
Suppose slope of PQ is m.
Equation of PQ is
y – 2 = m(x – 1)
= mx – m
mx – y + (2 – m) = 0 ……………. (1)

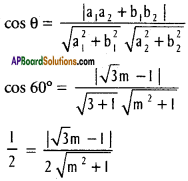
Squaring and cross multiplying
m² + 1 = (√3 – 1)²
= 3m² + 1 – 2√3m
2m² – 2√3m = 0
2m(m – √3) = 0
m = 0 or √3

Case (i) : m = 0
Equation of PQ is -y+2 = 0 or y-2 = 0

Case (ii): m = √3
Equation of PQ is √3x – y + (2 – √3) = 0

Question 3.
The base of an equilateral triangle is x + y – 2 = 0 and the opposite vertex is (2, -1). Find the equation of the remaining sides.
Solution:
ABC is an equilateral triangle.
∴ ∠B = C = 60°

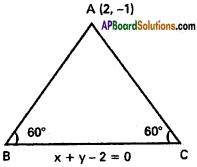
Equation of BC is x + y – 2 = 0
AB passes through A(2, -1)
Suppose slope of AB = m
Equation of AB is
y + 1 = m(x – 2)
= mx – 2m
mx – y – (2m + 1) = 0 …………. (1)

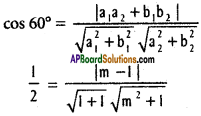
Squaring and cross multiplying
m² + 1 = 2 (m – 1)² = 2 (m² – 2m + 1)
= 2m² – 4m + 2
m² – 4m +1 = 0
\(m=\frac{4 \pm \sqrt{16-4}}{2}=\frac{4 \pm 2 \sqrt{3}}{2}=2 \pm \sqrt{3}\)
Substituting in (1)
Equation of AB is y + 1 = (2 + √3) (x – 2)
Equation of AC is y + 1 = (2 – √3) (x – 2)

Question 4.
Find the orthocentre of the triangle with following vertices.
i) (-2, -1), (6, -1) and (2, 5)
ii) (5,-2), (-1, 2) and (1, 4)
Solution:
i) A(-2, -1), B(6, -1), C(2,5) are the vertices of ∆ ABC.

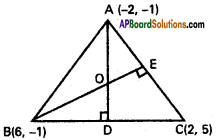
Slope of BC = \(\frac{5+1}{2-6}=\frac{6}{-4}=-\frac{3}{2}\)
AD is perpendicular to BC
Slope of AD = \(\frac{2}{3}\)
Equation of AD is
y + 1 = \(\frac{2}{3}\) (x + 2)
2x – 3y + 1 = 0 …………….. (1)
Slope of AC = \(\frac{5+1}{2+2}=\frac{6}{4}=\frac{3}{2}\)
BE is ⊥^lr to AC
Slope of BE = –\(\frac{2}{3}\)
Equation of BE is
y + 1 = – \(\frac{2}{3}\)(x – 6)
2x + 3y – 9 = 0 …………. (2)
By solving (1),(2)

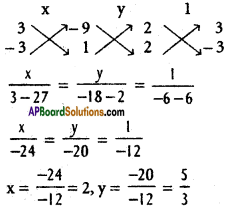
∴ Co-ordinates of the orthocentre
O are = (2, \(\frac{5}{3}\))

ii) (5, -2), (-1, 2) and (1, 4)
A(5, -2), B(-1, 2), C(1, 4) are the vertices of ∆ ABC.
Slope of BC = \(\frac{2-4}{-1-1}=\frac{-2}{-2}=1\)
AD is perpendicular to BC

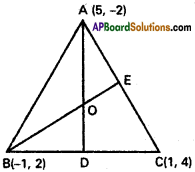
Slope of AD = –\(\frac{1}{m}\) = -1 m
Equation of AD is
y + 2 = -(x – 5)
= -x + 5
x + y – 3 = 0 …………. (1)
Slope of AC = \(\frac{4+2}{1-5}=\frac{6}{-4}=-\frac{3}{2}\)
BE is perpendicular to AC
Slope of BE is –\(\frac{1}{m}\) = \(\frac{2}{3}\)
Equation of BE is y – 2 = j(x + 1)
3y – 6 = 2x + 2
2x – 3y + 8 = 0 ……….. (2)
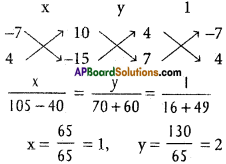
From (1), (2) by cross – multiplication law

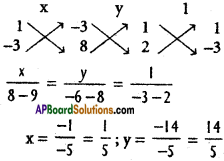
Co-ordinates of the Orthocentre O are (\(\frac{1}{5}\), \(\frac{14}{5}\))

Question 5.
Find the clrcumcentre of the triangle whose vertices are given below.
i) (-2, 3) (2, -1) and (4, 0)
ii) (1, 3), (0, -2) and (-3, 1)
Solution:
i) A(-2, 3), B(2, -1), C(4, 0) are the vertices of ∆ ABC.
D is the midpoint of BC

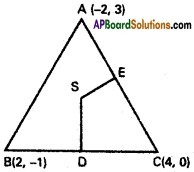
Co-ordinates of D are (\(\frac{2+4}{2}\), \(\frac{-1+0}{2}\)
= (3, \(\frac{-1}{2}\))
Slope of BC = \(\frac{-1-1}{2-4}=\frac{-1}{-2}=\frac{1}{2}\)
SD is perpendicular to BC
Slope of SD = –\(\frac{1}{m}\) = -2
Equation of SD is y + \(\frac{1}{2}\) = -2(x – 3)
2y + 1 = -4(x – 3)
= -4x+ 12
4x + 2y – 11 = 0 ………….. (1)
E is the midpoint of AC
Co-ordinates of E are (\(\frac{-2+4}{2}\), \(\frac{3+0}{2}\)) = (1, \(\frac{3}{2}\))
Slope of AC = \(\frac{3-0}{-2-4}=-\frac{3}{6}=-\frac{1}{2}\)
SE is perpendicular to AC
Slope of SE = –\(\frac{1}{m}\) = 2
Equation of SE is y – \(\frac{3}{2}\) = 2(x – 1)
2y- 3 = 4(x- 1)
= 4x – 4
4x – 2y – 1 = 0 ……………. (2)
4x + 2y – 11 = 0 ……………. (1)
Adding (1), (2) ⇒ 8x- 12 = 0
8x = 12
x = \(\frac{12}{8}\) = \(\frac{3}{2}\)
Substituting in (1)
2y = 11 – 4x = 11 – 4 . \(\frac{3}{2}\) = 11 – 6 = 5
y = \(\frac{5}{2}\)
∴ Co-ordinates of S are (\(\frac{3}{2}\), \(\frac{5}{2}\))

ii) (1, 3), (0, -2) and (-3, 1)

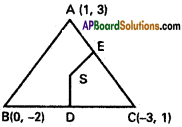
In ∆ ABC,
A = (1, 3), B = (0, -2), C = (-3, 1)
D is the midpoint of BC

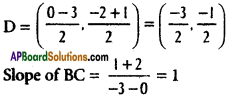
SD is ⊥^lr to BC
Slope of SD = 1
Equation of SD is
y + \(\frac{3}{2}\) = 1(x + \(\frac{3}{2}\))
⇒ 2y + 1 = 2x + 3
⇒ 2x – 2y + 2 = 0
⇒ x – y + 1 = 0 …………… (1)
E is the midpoint of CA
⇒ E = (\(\frac{-3+1}{2}\), \(\frac{1+3}{2}\)) = (-1, 2)
Slope of CA = \(\frac{1-3}{-3-1}\) = \(\frac{1}{2}\)
SE is ⊥^lr to CA
Slope of SE = -2
Equation of SE is
y – 2 = -2(x + 1)
⇒ y – 2 = -2x – 2
⇒ 2x + y = 0 …………….. (2)
By solving (1), (2)

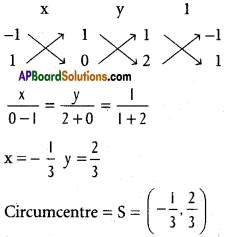
Question 6.
Let \(\overline{\mathrm{P S}}\) be the median of the triangle with vertices P(2, 2) Q(6, -1) and R(7, 3). Find the equation of the straight line passing through (1, -1) and parallel to the median \(\overline{\mathrm{P S}}\).

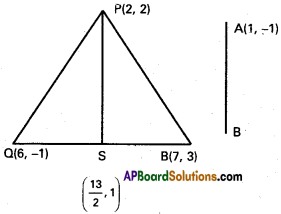
Solution:
P(2, 2), Q(6, -1), R(7, 3) are the vertices of ∆ ABC.
S is the mid point of QR

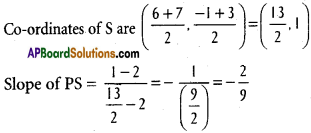
AB is parallel to PS and passes through A(1, -1)
Equation of AB is y + 1 = – \(\frac{2}{9}\) (x – 1)
9y + 9 = -2x + 2
2x + 9y + 7 = 0

III.

Question 1.
Find the orthocentre of the triangle formed by the lines.
x + 2y = 0, 4x + 3y – 5 = 0 and 3x + y = 0.

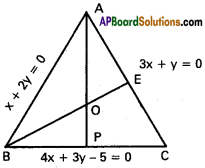
Solution:
Equation of AB is x + 2y = 0 ………….. (1)
Equation of BC is 4x + 3y – 5 = 0 ………….. (2)
Equation of AC is 3x + y = 0 ………….. (3)
Solving (1) and (2) Co-ordinates of A are (0, 0)

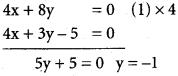
4x – 8 = 0 ⇒ 4x = 8, x=2
Co-ordinates of B are (2, -1)
Equation of BC is 4x + 3y – 5 = 0
AB is perpendicular to BC and passes through A(0, 0)
Equation of AB is 3x – 4y = 0 ……….. (1)
BE is perpendicular to AC
∴ Equation of BE is x – 3y = k
BE passes through B (2, -1)
2 + 3 = k ⇒ k = 5
Equation of BE is x – 3y – 5 = 0 …………………. (2)

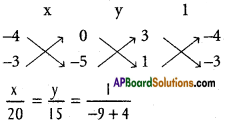
x = – 4, y = -3
∴ Orthocentre is O (- 4, -3)

Question 2.
Find the circumcentre of the triangle whose sides are given by x + y + 2 = 0, 5x – y – 2 = 0 and x – 2y + 5 = 0.
Solution:
Given lines are
x + y + 2 = 0 ………………. (1)
5x – y – 2 = 0 ………………. (2)
x – 2y + 5 = 0 ……………… (3)
Point of intersection of (1) and (2) is A = (0, -2)
Point of intersection of (2) and (3) is B = (1, 3)
Point of intersection of (1) and (3) is C = (-3, 1)
Let S = (α, β) the orthocentre of ∆ ABC then
SA = SB = SC
⇒ SA² = SB² = SC²
⇒ (α – 0)² + (β + 2)² = (α – 1)² + (β – 3)² = (α + 3)² + (β – 1)²

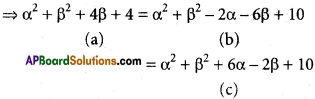
(a) = (b) ⇒ α² + β² + 4β + 4 = α² + β² – 2α – 6β + 10
⇒ 2α + 10β – 6 = 0
⇒ α + 5β – 3 = 0 ………. (4)

(a) = (c) => α² + β² + 4β + 4 = α² + β² + 6α – 2β + 10
⇒ 6α – 6β + 6 = 0
⇒ α – β + 1 = 0 ………….. (5)
From (4) and (5)

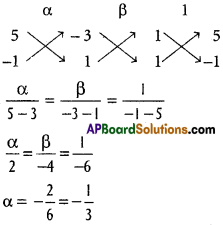
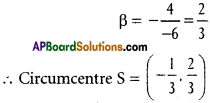
Question 3.
Find the equation of the straight lines passing through (1, 1) and which are at a distance of 3 units from (-2, 3).
Solution:
AB passes through A(1, 1)
Suppose slope of AB is m
Equation of AB is y – 1 = m(x – 1)
= mx – m
mx – y + (1 – m) = 0 ………….. (1)
Distance from (-2, 3) on AB = 3
\(\frac{|-2 m-3+1-m|}{\sqrt{m^{2}+1}}=3\)
Squaring and cross multiplying
(3m + 2)² = 9(m² + 1)
9m² + 4 + 12m = 9m² + 9
12m = 5 ⇒ m = \(\frac{5}{12}\)
Co-efficient of m² = 0 ⇒ m = ∞

i) m = ∞
AB is a vertical line
Equation of AB is x = a
AB passes through A(1, 1)
∴ a = 1
Equation of AB is x = 1 S

ii) m = \(\frac{5}{12}\)
substituting in (1),
Equation of AB is \(\frac{5}{12}\)x – y + [1 – \(\frac{5}{12}\)] = 0
\(\frac{5}{12}\)x – y + \(\frac{7}{12}\) = 0
5x – 12y + 7 = 0

Question 4.
If P and q are the lengths of the perpen-diculars from the origin to the straight lines x sec α + y cosec α = a and x cos α – y sin α = a cos 2α, prove that 4p² + q² = a².
Solution:
Equation of AB is x sec α + y cosec α = a
\(\frac{x}{\cos \alpha}+\frac{y}{\sin \alpha}=a\)
x sin α + y cos α = a sin α cos α
x sin α + y cos α – a sin α cos α = 0
p = length of the perpendicular from O on AB

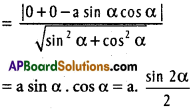
2p = asin 2α …………. (1)
Equation of CD is x cos α – y sin α = a cos 2α
x cos α – y sin α – a cos 2α = 0
q = Length of the perpendicular from O on CD
\(\frac{|0+0-a \cos 2 \alpha|}{\sqrt{\cos ^{2} \alpha+\sin ^{2} \alpha}}\) = cos2α ………. (2)
Squaring and adding (1) and (2)
4p² + q² = a² sin² 2α + a² cos² 2α
= a2 (sin² 2α + cos² 2α)
= a².1
= a²

Question 5.
Two adjacent sides of a parallelogram are given by 4x + 5y = 0 and 7x + 2y = 0 and one diagonal is 11x + 7y = 9. Find the equations of the remaining sides and the other diagonal.
Solution:
Let 4x + 5y = 0 ………… (1) and
7x + 2y – 0 ………… (2) respectively
denote the side \(\stackrel{\leftrightarrow}{O A}\) and \(\stackrel{\leftrightarrow}{O B}\) of the parallelo-gram OABC.
Equation of the diagonal \(\stackrel{\leftrightarrow}{A B}\) is 1 lx + 7y – 9 = 0 ………. (3)

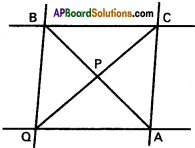
Solving (1) and (2) vertex O = (0, 0)
Solving (1) and (3), we get
Solving (2) and (3), we get

Midpoint of AB is P (\(\frac{1}{2}\), \(\frac{1}{2}\)), Slope of OP is 1.
Equation to OC is y = (1)x = x – y = 0
x = y

Question 6.
Find the incenter of the triangle formed by the following straight line.
i) x + 1 = 0, 3x- 4y = 5 and 5x + 12y = 27
ii) x + y – 7 =0, x – y + 1 = 0 and x – 3y + 5 = 0
Solution:
i)

In ∆ ABC,
Equation of side AC is
x + 1 = 0 ……… (1)
Equation of side AB is
3x – 4y – 5 = 0 ……………. (2)
Equation of side BC is
5x + 12y – 27 = 0 ………… (3)
From (1), x = – 1
Substitute in (2) ⇒ 3 (-1) – 4y – 5 = 0
4y = -8
y = -2
The point of intersection of (1), (2) is A =(-1, -2)
By solving (2), (3)

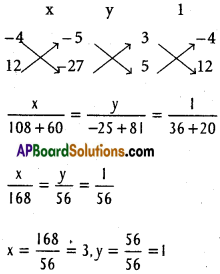
The point of intersection of (2), (3) is B = (3, 1)
From (1) x = -1
Substitute in (3)
-5 + 12y – 27 =0
12y = 32
y = \(\frac{32}{12}=\frac{8}{3}\)
The point of intersection of (3), (1) is

Incentre = I =

ii)

In ∆ ABC,
Equation of AC is x + y – 7 = 0 ………… (1)
Equation of AB is x – y + 1 = 0 ………… (1)
Equation of BC is x – 3y + 5 = 0 ………… (1)
solving (1) (2) and (3)
verti and A (3, 4) B (1, 2) and C (4, 3)

Question 7.
A ∆^le is formed by the lines ax + by + c = 0, lx + my + n = 0 and px + qy + r = 0. Given that the ∆^le is not right angled, show that the straight line \(\frac{a x+b y+c}{a p+b Q}=\frac{l x+m y+n}{I p+m Q}\) passes through the orthocentre of the ∆^le.
Solution:
Given sides of triangle are

ax+by+c /x+mv+y
ax + by + c = 0 ………… (1)
lx + my + n = 0 ………… (2)
px + qy + r = 0 ………… (3)
Equation of line passing through intersecting points of (1), (2) is
ax + by + c + k (lx + my + n) = 0 ………… (4)
(a + ki) x + (b + km)y + (c + nk) = 0
It is ⊥^lr to (3), then
p(a + kl) + q(b + km) = 0
⇒ k = –\(\frac{a P+b Q}{l p+m Q}\)
Substitute in (4)

is the required straight line equation of AD This is the altitude passing throught A.

Passes through the othrocentre of the triangle.

Question 8.
The Cartesian equations of the sides \(\overrightarrow{B C}\) , \(\overrightarrow{C A}\) and \(\overrightarrow{A B}\) of a ∆^le are respectively u₁ = a₁x + b₁y + c1 = 0, r = 1, 2, 3. Show that the equation of the straight line passing through A and bisecting the side \(\overline{\mathrm{B C}}\) is \(\frac{u_{3}}{a_{3} b_{1}-a_{1} b_{3}}=\frac{u_{2}}{a_{3} b_{1}-a_{1} b_{3}}\)
Solution:
A is a point of intersection of the lines u₂ = 0 and u₃ = 0
∴ Equation to a line passing through A is
u₂ + λu₃ = 0 ⇒ (a₂x + b₂y + c₂) + λ(a₃x + b₃y + c₃) = 0 ………….. (1)
⇒ (a₂ + λa₃)x + (b₂ + λb₃) y + (c₂ + λc₃) = 0
If this is parallel to a₁x + b₁y + c₁ = 0, we get
\(-\frac{\left(a_{2}+\lambda a_{3}\right)}{\left(b_{2}+\lambda b_{3}\right)}=-\frac{a_{1}}{b_{1}}\)
⇒ (a₂ + λa₃) b₁ = (b₂ + λb₃) a₁
⇒ a₂b₁ + λa₃b₁ = a₁b₂ + λa₁b₃
⇒ λ(a₃b₁ – a₁b₃) = – (a₂b₁ – a₁b₂) .
⇒ λ = \(\frac{\left(a_{2} b_{1}-a_{1} b_{2}\right)}{a_{3} b_{1}-a_{1} b_{3}}\)
Substituting this value of X in (1), the required equation is
(a₂x + b₂y + c₂) – \(\frac{\left(a_{2} b_{1}-a_{1} b_{2}\right)}{\left(a_{3} b_{1}-a_{1} b_{3}\right)}\) (a₃x + b₃y + c₃) = 0
⇒ (a₃b₁ – a₁b₃) (a₂x + b₂y + c₂) – (a₂b₁ – a₁b₂) (a₃x + b₃y + c₃) = 0
⇒ (a₃b₁ – a₁b₃)u₂ – (a₂b₁ – a₁b₂) u₃ = 0
⇒ (a₃b₁ – a₁b₃)u₂ = (a₂b₁ – a₁b₂)u₃
⇒ \(\frac{u_{3}}{\left(a_{3} b_{1}-a_{1} b_{3}\right)}=\frac{u_{2}}{\left(a_{2} b_{1}-a_{1} b_{2}\right)}\)