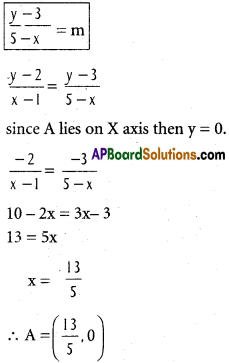Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B The Straight Line Solutions Exercise 3(d) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B The Straight Line Solutions Exercise 3(d)
I. Find the angle between the following straight lines.
Question 1.
y = 4 – 2x, y = 3x + 7
Solution:
y = 4 – 2x ⇒ 2x + y – 4 = 0
3x – y + 7 = 0
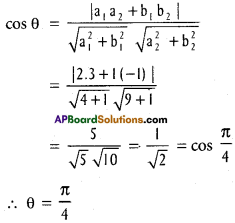
Question 2.
3x + 5y = 7, 2x – y + 4 = 0
Solution:
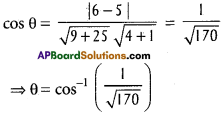
Question 3.
y = – √3 + 5, y = \(\frac{1}{\sqrt{3}} x-\frac{2}{\sqrt{3}}\)
Solution:
m1 = √3, m2= \(\frac{1}{\sqrt{3}}\)
m1m2 = (-√3).\(\frac{1}{\sqrt{3}}\) = 1
The lines are perpendicular θ = \(\frac{\pi}{2}\)
Question 4.
ax + by = a + b, a(x-y) + b(x + y) = 2b
Solution:
ax + by = a + b, (a + b) x + (- a + b) y = 2b

Find the length of the perpendicular drawn from the point given against the following straight lines.
Question 5.
5x – 2y + 4 = 0, (-2, -3)
Solution:
Length of the perpendicular
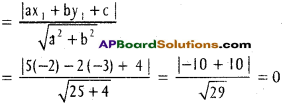
Question 6.
3x – 4y + 10 = 0, (3, 4)
Solution:
Length of the perpendicular
\(=\frac{|3.3-4.4+10|}{\sqrt{9+16}}=\frac{3}{5}\)
![]()
Question 7.
x – 3y – 4 = 0, (0,0)
Solution:
Length of the perpendicular
\(=\frac{|0-0-4|}{\sqrt{1+9}}=\frac{4}{\sqrt{10}}\)
Find the distance between the following parallel lines.
Question 8.
3x – 4y = 12, 3x – 4y = 7
Solution:
Equation of the lines are
3x – 4y – 12 = 0
3x – 4y – 7 = 0
Distance between parallel lines
\(=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}=\frac{|-| 2+7 \mid}{\sqrt{9+16}}=\frac{5}{5}=1\)
Question 9.
5x – 3y – 4 = 0, 10x – 6y – 9 = 0
Solution:
Equations of the lines can be taken as
10x – 6y – 8 = 0
10x – 6y – 9 = 0
Distance between parallel lines
\(=\frac{|-8+9|}{\sqrt{100+36}}=\frac{1}{2 \sqrt{34}}\)
Question 10.
Find the equation of the straight line parallel to the line 2x + 3y 4- 7 = 0 and passing through the point (5, 4).
Solution:
Equation of the given line is 2x + 3y + 7 = 0
The required line is parallel to this line
Equation of the parallel line is 2x + 3y = k
This line passes through p (5, 4)
10 + 12 = k ⇒ k = 22
Equation of the required line is
2x + 3y = 22
2x + 3y — 22 = 0
Question 11.
Find the equation of the straight line per-pendicular to the line 5x – 3y + 1 = 0 and passing through the point (4, – 3).
Solution:
Equation of the given line is 5x – 3y + 1 = 0
Equation of the perpendicular line is 3x + 5y + k = 0
This line passes through P (4, -3)
12 – 15 + k = 0 ⇒ k = 3
Equation of the required line is
3x + 5y + 3 = 0
Question 12.
Find the value of k, if the straight lines 6x – 10y + 3 = 0 and kx – 5y + 8 = 0 are parallel.
Solution:
Equations of the given lines are
6x – 10y + 3 = 0
kx – 5y + 8 = 0
These lines are parallel
a1b2 = a2b1
-30 = -10 k
k = 3
Question 13.
Find the value of p, if the straight lines 3x 4- 7y – 1 = 0 and 7x – py + 3 = 0 are mutually perpendicular.
Solution:
Equations of the given lines are
3x + 7y – 1 = 0
7x – py + 3 = 0
These lines are perpendicular
⇒ a1a2 + b1b2 = 0
3.7 + 7(- p) = 0
7p = 21 ⇒ p = 3
Question 14.
Find the value of k, if the straight lines y – 3kx + 4 = 0 and (2k-1) x-(8k-1) y – 6 = 0 are perpendicular.
Solution:
Equations of the given lines are
-3kx + y + 4 = 0
(2k- 1)x- (8k- 1)y- 6 = 0
These lines are perpendicular
⇒ -3k(2k – 1) – 1(8k – 1) = 0
– 6k² +.3k – 8k +1 = 0
6k² + 5k – 1 = 0
(k + 1) (6k – 1) = 0
k = -1 or 1/6
![]()
Question 15.
(- 4,5) is a vertex of a square and one of its diagonal is 7x – y + 8 = 0. Find the equation of the other diagonal.
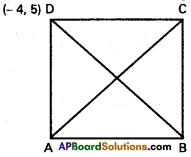
Solution:
ABCD is a square Equation of the diagonal AC is 7x – y + 8 = 0
The other diagonal BD is perpendicular to AC.
Equation of BD can be taken asx + 7y + k = 0
BD passes through D (- 4, 5)
-4 + 35 + k = 0 ⇒ k = 4-35 = -31
Equation of BD is x + 7y- 31 = 0
II.
Question 1.
Find the equations of the straight lines passing through (1, 3) and i) parallel to ii) perpendicular to the line passing through the points (3, -5) and (-6,1).
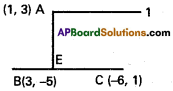
Solution:
A (3, -5), B(- 6, 1) are the given points
Slope of AB = \(\frac{-5-1}{3+6}=\frac{-6}{9}=\frac{-2}{3}\)
i) The required line is parallel to AB and passes through (1, 3)
Equation of the required line is
y – 3 = \(\frac{-2}{3}\)(x – 1)
3y – 9 = -2x + 2
2x + 3y – 11 = 0
ii) The required line AE is perpendicular to AD.
Equation of AE can be taken as 3x – 2y + k = 0
This line passes through A (1, 3)
3 – 6 + k = 0 ⇒ k = 6 – 3 = 3
Equation of AE is 3x – 2y + 3 = 0.
Question 2.
The line \(\frac{x}{a}-\frac{y}{b}\) = 1 meets the X-axis at P. Find the equation of the line perpen-dicular to this line at P.
Solution:
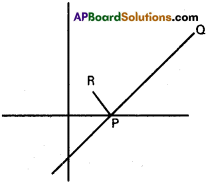
Equation of PQ is \(\frac{x}{a}-\frac{y}{b}\) = 1
Equation of X-axis is y = 0
\(\frac{x}{a}\) = 1 ⇒ x = a
Co-ordinates of P are (a, 0)
PR is perpendicular to PQ
Equation of PR = \(\frac{x}{b}+\frac{y}{a}\) = k
This line PR passes through P is (a, 0) a
\(\frac{a}{b}\) + 0 = k ⇒ k = a/b
Equation of PR is \(\frac{x}{b}+\frac{y}{a}=\frac{a}{b}\) = 1
![]()
Question 3.
Find the equation of the line perpendi-cular to the line 3x + 4y + 6 = 0 and making an intercept – 4 on X-axis.
Solution:
Equation of the given line is 3x + 4y + 6 = 0
Equation of the perpendicular line is
4x – 3y = k
\(\frac{4x}{k}-\frac{3y}{k}\) = 1
\(\frac{x}{\left(\frac{k}{4}\right)}+\frac{y}{\left(-\frac{k}{3}\right)}=1\)
x – intercept = \(\frac{k}{4}\) = – 4 ⇒ k = -16
Equation of the required line is 4x – 3y = -16
⇒ 4x – 3y + 16 = 0
Question 4.
A (-1,1), B (5, 3) are opposite vertices of a square in the XY plane. Find the equation of the other diagonal, (not passing through A, B) of the square.
Solution:
A (-1, 1), B (5, 3) are opposite vertices of the square.
Slope of AB \(\frac{1-3}{-1-5}=\frac{-2}{-6}=\frac{1}{3}\)
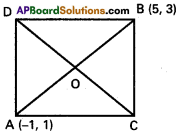
The other diagonal perpendicular to AB
Slope of CD = – \(\frac{1}{m}\) = -3 m
‘O’ is the point of intersection of the diagonals
Co-ordinates of O are\(\left(\frac{-1+5}{2}. \frac{1+3}{2}\right)\) = (2, 2)
CD passes through O (2, 2)
Equation of CD is y – 2 = -3 (x – 2)
= -3x + 6
3x + y – 8 = 0
Question 5.
Find the foot of the perpendicular drawn from (4, 1) upon the straight line 3x – 4y + 12 = 0.
Solution:
Equation of the line is 3x – 4y + 12 = 0
If (x2, y2) is the foot of the perpendicular from (x1, y1) on the line
ax + by + c = 0, then
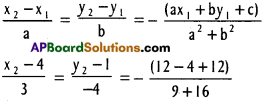

Question 6.
Find the foot of the perpendicular drawn from (3, 0) upon the straight line 5x + 12y – 41 = 0.
Solution:
Equation of the line is 5x + 12y – 41 = 0
If (x2, y2) is the foot of the perpendicular from (x1, y1) on the line ax + by + c = 0,

Question 7.
x – 3y – 5 = 0 is the perpendicular bisector of the line segment joining the points A, B. If A = (-1, -3), find the co-ordinates of B.
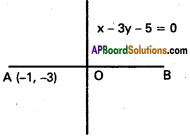
Solution:
If PQ is the perpendicular bisector of AB, then B is the image of A in the line PQ.
Equation of PQ is x – 3y – 5 = 0
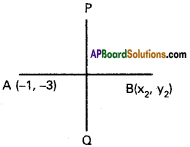
Co-ordinates of A are (-1, -3)
If (x2, y2) is the image of (x1, y1) about the line ax + by + c = 0, then

Question 8.
Find the image of the point (1, 2) in the straight line 3x + 4y – 1 = 0,
Solution:
Equation of the line is 3x + 4y – 1 = 0 ‘
If (x2, y2) is the image of (x1, y1) in the line ax + by + c = 0, then
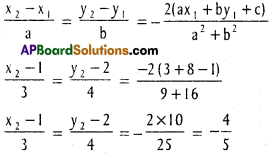

Question 9.
Show that the distance of the point (6, – 2) from the line 4x + 3y = 12 is half the distance of the point (3,4) from the line 4x – 3y = 12.
Solution:
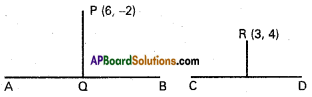
Equation of AB is 4x + 3y – 12 = 0
PQ = Length of the perpendicular from
\(P=\frac{|24-6-12|}{\sqrt{16+9}}=\frac{6}{5}\)
Equation of CD is 4x – 3y – 12 = 0
RS = Length of the perpendicular from
\(R=\frac{|12-12-12|}{\sqrt{16+9}}=\frac{12}{5}\)
∴ PQ = \(\frac{1}{2}\)RS
![]()
Question 10.
Find the locus of the foot of the perpendi¬cular from the origin to a variable straight line which always passes through a fixed point (a, b).
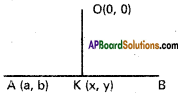
Solution:
Suppose m is the slope of the line AB
Equation of AB is y – b = m (x – a)
= mx – ma
mx – y + (b – ma) = 0 ……………. (1)
OK is perpendicular to A B and passes through the origin O. Suppose co-ordinates of K are (x, y)
Equation of AB is x + my – 0 ……………. (2)

m = -x/y
Substituting in (1)
\(-\frac{x^{2}}{y}-y+b+\frac{x}{y} \cdot a=0\).
– x² – y² + by + ax = 0
or x² + y² – ax – by = 0
Locus of K is x² + y² – ax – by = 0
III.
Question 1.
Show that the lines x – 7y – 22 = 0, 3x + 4y + 9 = 0 and 7x + y – 54 = 0 form a right angled isosceles triangle.
Solution:
Given lines x – 7y – 22 = 0 …………. (1)
3x + 4y + 9 = 0 …………. (2)
7x + y – 54 = 0 …………. (3)
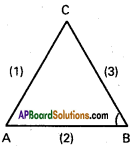
Let ‘A’ be the angle between (1), (2)
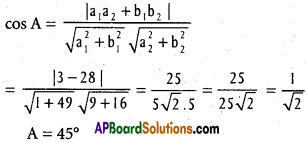
Let B be the angle between (2), (3)

Let ‘C’ be the angle between (3), (1)
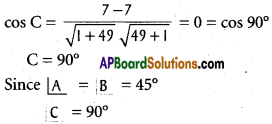
∴ Given lines form a right angled isosceles triangle.
Question 2.
Find the equation of the straight lines passing through the point (-3, 2) and making an angle of 45° with the straight line 3x – y + 4 = 0.
Solution:
Given point
P(x1, y1) = (-3, 2)
Given line 3x – y + 4 = 0 ………….. (1)
Slope = m = – \(\frac{a}{b}\) = 3
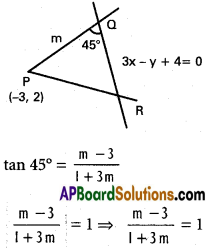
m – 3 = -1 + 3m
2m = – 4 or m = -2
\(\frac{m-3}{1+3 m}\) = -1 ⇒ m – 3 = -1 – 3m
4m = 2 ⇒ m = 1/2
Case (i) m = – 2
Equation of the line PQ is
y – 2 = -2(x+3)
= -2x – 6
2x + y + 4 = 0
Case (ii) m =\(\frac{1}{2}\)
Equation of the line PR is
y – 2 = \(\frac{1}{2}\) (x + 3)
2y – 4 = x + 3
x – 2y + 7 = 0
Question 3.
Find the angles of the triangle whose sides are x + y- 4 = 0,2x + y- 6 = 0, 5x + 3y -15 = 0.
Solution:
Equation of AB is x + y – 4 = 0
Equation of BC is 2x + y – 6 = 0
Equation of AC is 5x + 3y – 15 = 0

Question 4.
Proye that the feet of the perpendiculars from the origin on the lines x + y = 4, x + 5y = 26 and 15x – 27y = 424 are collinear.
Solution:
Given lines
x + y – 4 = 0 ……… (1)
x + 5y – 26 = 0 ……… (2)
15x – 27y – 424 = 0 ……… (3)
Let P(x2, y2) be the foot of the ⊥le of (x1, y1) = (0, 0) on (1)
![]()
⇒ x2 – 0 = 2, y2 – 0 = 2
⇒ x2 = 2, y2 = 2
∴ P = (2, 2)
Let Q(x3, y3) be the foot of the ⊥le of (x1 y1) = (0, 0) on (2)
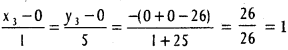
x3 = 1, y3 = 5 ⇒ Q = (1, 5)
Let R(x4, y4) be the foot of the ⊥le of (x1, y1) = (0, 0) on (3)

Equation of the line through P,Q is
\(\frac{x-2}{1-2}=\frac{y-2}{5-2}\) ⇒ 3x + y – 8 = 0 ………. (4)
Substitute R (x4, y4) in (4)
⇒ 3\(\frac{1060}{159}\) – 12 – 8
= 20 – 20 = 0
∴ Foot of perpendiculars of origin on the lines lies on a straight line.
![]()
Question 5.
Find the equations of the straight lines passing through the point of intersection of the lines 3x + 2y + 4 = 0,2x + 5y = 1 and whose distance from (2, -1) is 2.
Solution:
Equations of the lines passing through the point of intersection of the line
L1 ≡ 3x + 2y + 4 = 0, L3 ≡ 2x + 5y – 1 = 0 is
L1 + λL2 = 0
(3x + 2y + 4) + λ (2x + 5y- 1) = 0
(3 + 2λ)x + (2 + 5λ) y + (4 – λ) = 0 ………….. (1)
Given distance from (2, -1) to (1) = 2
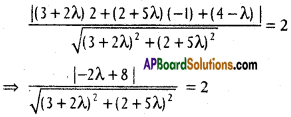
⇒ (-λ + 4)2 = 9 + 4λ2 + 12λ + 4 + 25λ2 + 20λ
⇒ 28λ2 + 40λ – 3 = 0
⇒ 28λ2 – 2λ + 42λ – 3 = 0
⇒ (2λ + 3) (14λ – 1) = 0
⇒ λ = \(\frac{1}{14}\), λ = – \(\frac{3}{2}\)
From (1)
If λ = \(\frac{1}{14}\) ⇒ 4x + 3y + 5 = 0
If λ = – \(\frac{3}{2}\)
⇒ y – 1 = 0 are the required line equations.
Question 6.
Each side of a square is of length 4 units. The centre of the square is (3, 7) and one of its diagonals is parallel to y = x. Find the co-ordinates of its vertices.
Solution:
Let ABCD be the square.
Point of intersection of the diagonals is the centre P(3, 7)
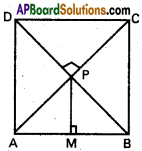
From P draw PM⊥AB. Then M is midpoint ofAB
∴ AM = MB = PM = 2
Since a diagonal is parallel to y = x, its sides are parallel to the co-ordinate axes.
M(3, 5) ⇒ A(1, 5), B(5, 5), C(5, 9), D(1, 9)
Question 7.
If ab > 0, find the area of the rhombus enclosed by the four straight lines ax ± by ± c = 0.
Solution:
Equation of AB is ax + by + c = 0 ………….. (1)
Equation of CD is ax + by – c = 0 ………….. (2)
Equation of BC is ax – by + c = 0 ………….. (3)
Equation of AD is ax – by – c = 0 ………….. (4)
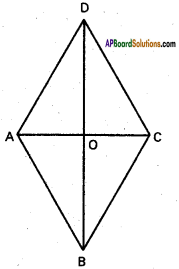
Solving (1) and (3), co-ordinates of B are (-\(\frac{c}{a}\) 0)
Solving (1) and (4) co-ordinates of A are (0, –\(\frac{c}{b}\)
Solving (2) and (3) co-ordinates of C are (0, \(\frac{c}{b}\)
Solving (2) and (4) co-ordinates of D are (\(\frac{c}{a}\), 0)
Area of rhombus ABCD = \(\frac{1}{2}\)|∑x1 (y2 – y4)|
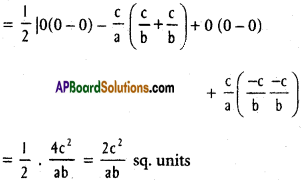
Question 8.
Find the area of the parallelogram whose sides are 3x + 4y + 5 = 0, 3x + 4y – 2 = 0, 2x + 3y + 1 = 0 and 2x + 3y – 7 = 0
Solution:
Given sides are 3x + 4y + 5 = 0 ……….. (1)
3x + 4y – 2 = 0 ……….. (2)
2x + 3y + 1 = 0 ……….. (3)
2x + 3y – 7 = 0 ……….. (4)
Area of parallelogram formed by (1), (2), (3), (4)

Question 9.
A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find the equation of the path the he should follow.
Solution:
By solving
2x – 3y + 4 = 0
3 x + 4y – 5 = 0
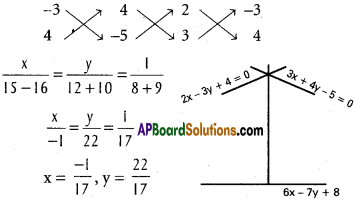
Given line 6x – 7y + 8 = 0
Required line is 7x + 6y + k = 0 …….. (1)

From (1) 7x + 6y – \(\frac{125}{17}\)
119x + 102y – 125 = 0
![]()
Question 10.
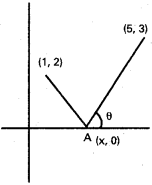
A ray of light passing through the point (1, 2) reflects on the X – axis at a point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.
Solution:
Let m be the slope then equation of line passing through (1, 2).
y – 2 = m(x – 1)
\(\frac{y-2}{x-1}=m\)
Let -m be the slope the equation of line passing through (5, 3)
y – 3 = -m(x – 5)