Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(b) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(b)
I.
Question 1.
Find the angle between the lines represented by 2x² + xy – 6y² + 7y – 2 = 0.
Solution:
Comparing with
ax² + 2hxy + by² + 2gx + 2fy + c = 0
a = 2, 2g = 0, g = 0
b = – 6, 2f = 7, f = 7/2
c = – 2, 2h = 1, h = 1/2
Angle between the lines is given by

Question 2.
Prove that the equation 2x² + 3xy – 2y² + 3x + y + 1 = 0 represents a pair of perpendicular lines.
Solution:
Given a = 2, b = -2
a + b = 0 ⇒ cos α = 0 ⇒ α = π/2
∴ The given lines are perpendicular.
![]()
II.
Question 1.
Prove that the equation 3x² + 7xy + 2y² + 5x + 5y + 2 = 0 represents a pair of straight lines and find the co-ordinates of the’point of intersection.
Solution:
The given equation is
3x² + 7xy + 2y² + 5x + 5y + 2 = 0
Comparing a = 3 2f = 5 ⇒ f = \(\frac{5}{2}\)
b = 2 2g = 5 ⇒ g = \(\frac{5}{2}\)
c = 2 2h = 7 ⇒ h = \(\frac{7}{2}\)
∆ = abc + 2fgh – af² – bg² – ch²
= 3(2)(2) + 2.\(\frac{5}{2}\).\(\frac{5}{2}\).\(\frac{7}{2}\) – 3.\(\frac{25}{4}\) – 2.\(\frac{25}{4}\) – 2.\(\frac{49}{4}\) = 0
= \(\frac{1}{4}\)(48 + 175 – 75 – 50 – 98)
= \(\frac{1}{2}\)(223 – 223) = 0

∴ The given equation represents a pair of lines point of intersection is

Question 2.
Find the value of k, if the equation 2x² + kxy – 6y² + 3x + y + l = 0 represents a pair of straight lines. Find the point of intersection of the lines and the angle between the straight lines for this value of k.
Solution:
The given equation is
2x² + kxy – by² + 3x + y+ 1 = 0
a = 2 2f = 1 ⇒ f = \(\frac{1}{2}\)
b = -6 2g = 3 ⇒ g = \(\frac{3}{2}\)
c = 1 2h = k ⇒ h = \(\frac{k}{2}\)
The given equation represents a pair of straight lines abc + 2fgh – af² – bg² – ch² = 0
-12 + 2.\(\frac{1}{2}\).\(\frac{3}{2}\)(+\(\frac{k}{2}\) -2.\(\frac{1}{4}\) + 6.\(\frac{9}{4}\) – \(\frac{k^{2}}{4}\) = 0
– 48 + 3k – 2 + 54 – k² = 0
-k² + 3k + 4 = 0 ⇒ k² – 3k – 4 = 0
(k – 4) (k + 1) = 0
k = 4 or – 1.
Case (i): k = – 1
Point of’intersection is \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)

Point of intersection is (\(\frac{-5}{7}\), \(\frac{1}{7}\))
Angle between the lines

Case (ii): k = 4
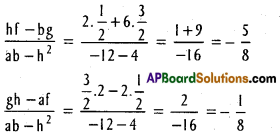
Point of intersection is P(-\(\frac{5}{8}\), –\(\frac{1}{8}\))
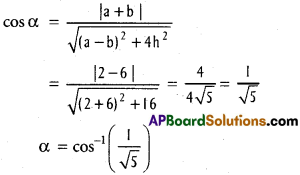
Question 3.
Show that the equation x² – y² – x + 3y – 2 = 0 represents a pair of perpendicular lines and find their equations.
Solution:
Comparing a= 1, f = \(\frac{3}{2}\)
b = -1, g = –\(\frac{1}{2}\)
c = -2, h = 0
abc + 2fgh – af² – bg² – ch²
= 1 (-1) (-2) + 0- 1.\(\frac{9}{4}\) + 1.\(\frac{1}{4}\) + 0
= + 2 – \(\frac{9}{4}\) + \(\frac{1}{4}\) = 0
h² – ab = 0 – 1(-1) = 1 > 0,
f² – be = \(\frac{9}{4}\) – 2 = \(\frac{1}{4}\) = 1 > 0
g² – ac = \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\) > 0
a + b = 1 – 1 = 0
The given equation represent a pair of per-pendicular lines
Let x² – y² – x + 3y – 2
= (x + y + c1) (x – y + c2)
Equating the co-efficients of x
⇒ c1 + c2 = – 1
Equating the co-efficients of y
⇒ – c1 + c2 = 3
Adding 2c2 = 2 ⇒ c2 = 1
c1 + c2 = – 1 ⇒ c1 + 1 = – 1
c1 = – 2
Equations of the lines are x + y – 2 = 0 and x – y + 1 = 0
![]()
Question 4.
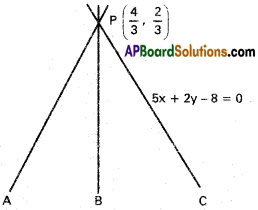
Show that the lines x² + 2xy – 35y² – 4x + 44y – 12 = 0 are 5x + 2y – 8 = 0 are concurrent.
Solution:
Equations of the given lines are
x² + 2xy- 35y² -4x + 44y- 12 = 0
a = 1, f = 22
b = – 35, g = – 2
c = – 12, h = 1
Point or intersection is \(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)

Point of intersection of the given lines is P(\(\frac{4}{3}\), \(\frac{2}{3}\))
5x + 2y – 8 = 5.\(\frac{4}{3}\) + 2.\(\frac{2}{3}\) – 8
= \(\frac{20+4-24}{3}\) = 0
P lies on the third line 5x + 2y – 8 = 0
∴ The given lines are concurrent.
Question 5.
Find the distances between the following pairs of parallel straight lines :
i) 9x² – 6xy + y² + 18x – 6y + 8 = 0
Solution:
Distance between parallel lines = \(2 \sqrt{\frac{g^{2}-a c}{a(a+b)}}\)

ii) x² + 2√3xy + 3y² – 3x – 3√3y – 4 = 0
Solution:
Distance between parallel lines = \(2 \sqrt{\frac{g^{2}-a c}{a(a+b)}}\)
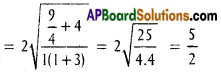
Question 5.
Show that the two pairs of lines 3x² + 8xy – 3y² = 0 and 3x² + 8xy – 3y² + 2x – 4y – 1 = 0 form a square.
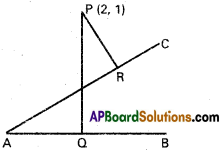
Solution:
Combined equation of CA and CB is
3x² + 8xy – 3y²
(x + 3y) (3x – y) = 0
3x – y = 0, x + 3y = 0
Equation of OA is 3x – y = 0 ………. (1)
Equation of OB is x + 3y = 0 ……….(2)
Combined equation of CA and CB is
3x² + 8xy – 3y² + 2x – 4y + 1 =0
Let 3x² + 8xy – 3y² + 2x – 4y + 1 = (3x – y + c1) (x + 3y + c2)
Equating the co-efficients of
x, we get c1 + 3c2 = 2
y, we have 3c1 + c2 = -4
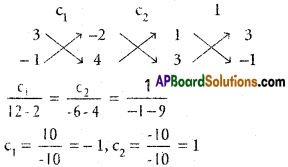
Equation of BC is 3x – y – 1 = 0 ………. (3)
Equation of AC is x + 3y + 1 = 0 ………. (4)
OA and BC differ by a constant ⇒ OA parallel to BC
OB and CA differ by a constant ⇒ OB parallel to AC
From combined equation of OA and OB
OACB is a rectangle a + b = 3 – 3 = 0
OA = Length of the -L lar from O to AC = \(\frac{|0+0+1|}{\sqrt{1+9}}=\frac{1}{\sqrt{10}}\)
OB = Length of the perpendicular from O to BC = \(\frac{|0+0-1|}{\sqrt{9+1}}=\frac{1}{\sqrt{10}}\)
OA = OB and OACB is a rectangle
OACB is a square.
III.
Question 1.
Find the product of the lengths of the perpendiculars drawn from (2, 1) upon the lines
12x² + 25xy + 12y² + 10x + 11y + 2 = 0

Solution:
Combined equation of AB, AC is
12x² + 25xy+ 12y² + 10x + 11y + 2 = 0
12x² + 25xy +12y²
= 12x² + 16xy + 9xy + 12y² = 0
= 4x (3x + 4y) + 3y (3x + 4y)
= (3x + 4y) (4x + 3y)
Let 12x² + 25xy + 12y² + 10x + 11y + 2
= (3x + 4y + c1) (4x + 3y + c2)
Equating the co-efficients of x, we get
4c1 + 3c2 = 10 ………. (1)
Equating the co-efficients of y, we get
3c1 + 4c2 = 11 ………… (2)
i.e., 4c1 + 3c2 – 10 = 0
3c1 + 4c2 – 11 = 0
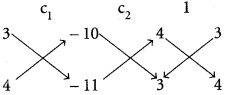
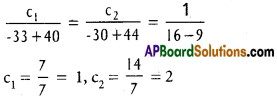
Equation of AB is 3x + 4y + 1 = 0
Equation of AC is 4x + 3y + 2 = 0
PQ = Length of the perpendicular from P(2, 1) on
AB = \(\frac{6+4+1}{\sqrt{9+16}}=\frac{11}{5}\)
PQ = Length of the perpendiculars from P(2, 1) on
AC = \(\frac{|8+3+2|}{\sqrt{16+9}}=\frac{13}{5}\)
Product of the length of the perpendiculars
= PQ × PR= \(\frac{11}{5}\) × \(\frac{13}{5}\) = \(\frac{143}{25}\)
![]()
Question 2.
Show that the straight lines y² – 4y + 3 = 0 and
x² + 4xy + 4y² + 5x + 10y + 4 = 0 form a parallelogram and find the lengths of its sides.
Solution:
Equation of the first pair of lines is
y² – 4y + 3 = 0
(y – 1) (y – 3) = 0
y – 1 = 0 or y – 3 = 0
Equation of AB is y – 1 = 0 ……….. (1)
Equation of CD is y – 3 = 0 ………. (2)
Equations of AB and CD differ by a constant.
∴ AB and CD are parallel.
Equation of the second pair of lines is
x² + 4xy + 4y² + 5x + 10y + 4 = 0
(x + 2y)² + 5(x + 2y) + 4 = 0
(x + 2y)² + 4 (x + 2y) + (x + 2y) + 4 = 0
(x + 2y)(x + 2y + 4) + 1(x + 2y + 4) = 0
(x + 2y + 1) (x + 2y + 4) = 0
x + 2y + 1 = 0, x + 2y + 4 = 0
Equation of AD is x + 2y + 1 = 0 ……… (3)
Equation of BC is x + 2y + 4 = 0 ……… (4)
AD and BC are parallel.
Solving (1), (3) x + 2 + 1 = 0
x = – 3
Co-ordinates of A are (-3, 1)
Solving (2), (3) x + 6 + 1 = 0
x = -7
Co-ordinates of DC are (-7, 3)
Solving (1), (4) x + 2 + 4 = 0
x = – 6
Co-ordinates of B are (-6, 1)

Lengths of the sides of the parallelogram are 3, 2√5.
Question 3.
Show that the product of the perpendicular distances from the origin to the pair of straight lines represented by ax² + 2hxy + by² + 2gx + 2fy + c = 0 is \(\frac{|c|}{\sqrt{(a-b)^{2}+4 h^{2}}}\)
Solution:
Let ax² + 2hxy + by² + 2gx + 2fy + c = 0 represents the lines
l1x + m1y + n1 = 0 ……….. (1)
l2x + m2y + n2 = 0 ………. (2)
⇒ ax² + 2hxy + by² + 2gx + 2fy + c ≡ (l1x + m1y + n1) (l2x + m2y + n2)
l1l2 = a, m1m2 = b, l1m2 + l2m1 = 2h,
l1n2 + l2n1 = 2g, m1n2 + m2n1 = 2f, n1n2 = c
⊥Ir distance from origin to (1) is = \(\frac{\left|n_{1}\right|}{\sqrt{l_{1}^{2}+m_{1}^{2}}}\)
⊥Irdistance from origin to (2) is = \(\frac{\left|n_{2}\right|}{\sqrt{I_{2}^{2}+m_{2}^{2}}}\)
Product of perpendiculars
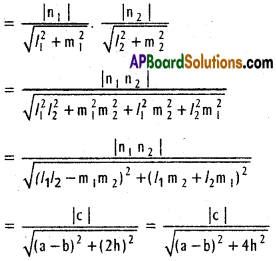
![]()
Question 4.
If the equation ax² + 2hxy + by² + 2gx + 2fy + c = 0 represents a pair of intersecting lines, then show that the square of the distance of their point of intersection from the origin is \(\frac{c(a+b)-f^{2}-g^{2}}{a b-h^{2}}\). Also slow that the square of this distance is \(\frac{f^{2}+g^{2}}{h^{2}+b^{2}}\) if the given lines are perpendicular.
Solution:
Let the equation
ax² + 2hxy + by² + 2gx + 2fy + c = 0
represent the lines
l1x + m1y + n1 = 0 …….. (1)
l2x + m2y + n2 = 0 …….. (2)
(l1x + m1y + n1)(l2x + m2y + n2) = ax² + 2hxy + by² + 2gx + 2fy + c
l1l2 = a, m1 m2 = b, n1n2 = c
l1m2 + l2m1 = 2h, l1n2 + l12n1 = 2g, m1n2 + m2n1 = 2f
Solving (1) and (2)
\(\frac{x}{m_{1} n_{2}-m_{2} n_{1}}=\frac{y}{I_{2} n_{1}-l_{1} n_{2}}=\frac{1}{l_{1} m_{2}-I_{2} m_{1}}\)
The point of intersection, P


If the given pair of lines are perpendicular, then a + b = 0
∴ a = -b
\(\mathrm{OP}^{2}=\frac{0-r^{2}-g^{2}}{(-b) b-h^{2}}=\frac{r^{2}+g^{2}}{h^{2}+b^{2}}\)