Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(e) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(e)
I.
Question 1.
Is the function f, defined by \(f(x)=\left\{\begin{array}{l}
x^{2} \text { if } x \leq 1 \\
x \text { if } x>1
\end{array}\right.\) continuous on R?
Solution:

f is continuous at x = 1
f is continuous on R.
Question 2.
Is f defined by f(x) = \(=\left\{\begin{array}{cc}
\frac{\sin 2 x}{x}, & \text { if } x \neq 0 \\
1 & \text { if } x=0
\end{array}\right.\) continuous at 0?
Solution:
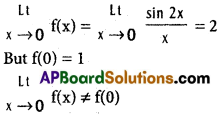
f is not continuous at 0
![]()
Question 3.
Show that the function f(x) = [cos (x10 + 1)]1/3, x ∈ R is a continuous function.
Solution:
We know that cos x is continuous for every x ∈ R
∴ The given function f(x) is continuous for every x ∈ R.
II.
Question 1.
Check the continuity of the following function at 2.

Solution:

f(x) is not continuous at 2.
Question 2.
Check the continuity of f given by f(x) = \(\begin{cases}\frac{\left[x^{2}-9\right]}{\left[x^{2}-2 x-3\right]} & \text { if } 0<x<5 \text { and } x \neq 3 \\ 1.5 & \text { if } x=3\end{cases}\) at the point 3.
Solution:
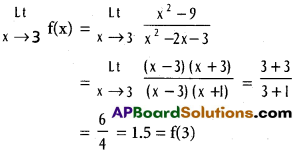
f(x) is continuous at x = 3.
Question 3.
Show that f, given by f(x) = \(\frac{x-|x|}{x}\) (x ≠ 0) is continuous on R – {0}.
Solution:
Case (i) : a > 0 ⇒ |a| = a

![]()
If x = 0, f(a) is not defined
f(x) is not continuous at ’0′
∴ f(x) is continuous on R – {0}
![]()
Question 4.
If f is a function defined by
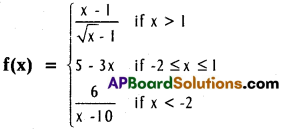
then discuss the continuity of f.
Solution:
Case (i) : x = 1

f(x) is not continuous at x > 1
Case (ii) : x = -2

f(x) is not continuous at x = -2.
Question 5.
If f is given by f(x) = \(=\left\{\begin{array}{cl}
k^{2} x-k & \text { if } x \geq 1 \\
2 & \text { if } x<1
\end{array}\right.\) is a continuous function on R, then find the values of k.
Solution:

2 = k² – k
k² – k – 2 = 0
(k – 2) (k + 1) = 0
k = 2 or – 1
Question 6.
Prove that the functions ‘sin x’ and ‘cos x’ are continuous on R.
Solution:
i) Let a ∈ R
![]()
∴ f is continuous at a.
ii) Let a ∈ R
![]()
∴ f is continuous at a.
III.
Question 1.
Check the continuity of ‘f given by

at the points 0, 1 and 2.
Solution:
i) ![]()
∴ f(x) is continuous at x = 0
ii) ![]()
∴ f(x) is continuous at x = 1
iii) 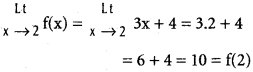
∴ f(x) is continuous at x = 2
![]()
Question 2.
Find real constant a, b so that the function f given by
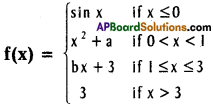
is continuous on R.
Solution:
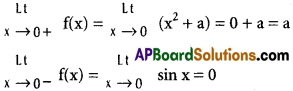
Since f(x) is continuous on R
LHS = RHS ⇒ a = 0
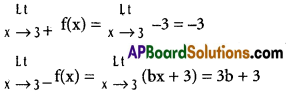
Since f(x) is continuous on R.
LHS = RHS
3b + 3 = -3
3b = – 6 ⇒ b = -2
Question 3.
Show that
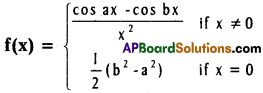
where a and b are real constants, is continuous at 0.
Solution:

∴ f(x) is continuous at x = 0