Inter 1st Year Maths 1B Differentiation Solutions Ex 9(d)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Differentiation Solutions Exercise 9(d) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Differentiation Solutions Exercise 9(d)

I.

Question 1.
If y = \(\frac{2x+3}{4x+5}\) then find y”
Solution:
y = \(\frac{2x+3}{4x+5}\)
Differentiating w.r.to x

Question 2.
y = ae^nx + be^-nx nx then prove that y” = n²y
Solution:
y = ae^nx + be^-nx
y₁ = na e^nx – nb e^-nx
y_{2 = n² . ae^nx + n² be^-nx
y”= n² (ae^nx + b.e^-nx)
= n²y}

II.

Question 1.
Find the second order derivatives of the following functions f(x)
i) cos³ x
Solution:
y = cos³ x = \(\frac{1}{4}\) [cos 3x + 3 cos x]
y’ = \(\frac{1}{4}\) [- 3 sin 3x – 3 sin x]
y” = \(\frac{1}{4}\) (- 9 cos 3x – 3 cos x)
= – \(\frac{1}{4}\) (3 cos x + 9 cos 3x)
= – \(\frac{3}{4}\) (cos x + 3 cos 3x)

ii) y = sin⁴ x
Solution:
y = sin⁴ x = (sin²x)² = (\(\frac{(1-\cos 2 x)^{2}}{2}\))
= \(\frac{1}{4}\) [1 – 2 cos 2x + cos² 2x]
= \(\frac{1}{4}\) [1 – 2cos 2x + \(\frac{1+\cos 4 x}{2}\)]
= \(\frac{1}{8}\) [2 – 4 cos 2x + 1 + cos 4x]
= \(\frac{1}{8}\)(3 – 4 cos 2x + cos 4x)
y’ = \(\frac{1}{8}\) (8 sin 2x – 4 sin 4x)
y” = \(\frac{1}{8}\) (16 cos 2x-16 cos 4x)
= 2 (cos 2x – cos 4x)

iii) log (4x² – 9)
Solution:
y = log (4x² – 9)
= log (2x – 3) (2x + 3)
= log (2x – 3) + log (2x + 3)

iv) y = e^-2x sin³ x
Solution:
y = e^-2x. sin³ x
y’ = e^-2x (3 sin² x. cos x) + sin3 x (e^-2x) (-2)
= e^-2x [3 sin² x. cos x – 2 sin³ x)
\(\frac{d^{2} y}{d x^{2}}\) = e^-2x [3 sin² x (- sin x) + 3 cos x (2 sin x) cos x – 6 sin² x cos x) – 2. e^-2x
[3 sin² x. cos x – 2 sin³ x]
= e^-2x [6 sin x. cos² x – 6 sin² x. cos x – 3 sin³ x. – 6 sin² x. cos x + 4 sin³ x)
= e^-2x [sin³ x – 12 sin² x. cos x + 6 sin x. cos² x)

v) e^x sin x cos 2x
Solution:
y = e^x. sin x. cos 2x = \(\frac{e^{x}}{2}\) (2 cos 2x. sin x)
= \(\frac{e^{x}}{2}\) (sin 3x – sin x)
y’ = \(\frac{1}{2}\) [e^x(3 cos 3x – cos x) + e^x (sin 3x – sin x)
y”= \(\frac{1}{2}\) [ex (- 9 sin 3x + sin x) + e^x (3 cos 3x – cos x) + e^x (3 cos 3x – cos x) + e^x (sin 3x – sin x)]
= \(\frac{e^{x}}{2}\) [- 9 sin 3x + sin x + 3 cos 3x – cos x + 3 cos 3x cos x + sin 3x – sin x]
= \(\frac{e^{x}}{2}\) [6 cos 3x – 8 sin 3x – 2 cos x]
= e^x [3 cos 3x – 4 sin 3x – cos x]

vi) Tan^-1\(\frac{1+x}{1-x}\)
Solution:
y = tan^-1\(\frac{1+x}{1-x}\)
Put x = tan θ

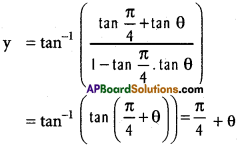
∴ f(x) = \(\frac{\pi}{4}\) + tan^-1 (x)
Diff. w.r.to x
f'(x) = 0 + \(\frac{1}{1+x^{2}}\)
f”(x) = (-1) (1 + x²)^-2 (2x)
f”(x) = \(\frac{-2 x}{\left(1+x^{2}\right)^{2}}\)

vii) tan^-1\(\frac{3x-x^{3}}{1-3x^{2}}\)
Solution:
f(x) = tan^-1\(\frac{3x-x^{3}}{1-3x^{2}}\) ; Put x = tan θ
f(x) = tan^-1\(\left(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\right)\)
= tan^-1(tan 3θ) = 3θ
∴ f(x) = tan^-1 (x)
f'(x) = 3\(\frac{1}{1+x^{2}}\) = \(\frac{3}{1+x^{2}}\)
Again Diff. w.r.to x
f”(x) = (3) (-1) (1 + x²)^-2 (2x)
⇒ f”(x) = \(\frac{-6 x}{\left(1+x^{2}\right)^{2}}\)

II. Prove the following.
If y = ax^{n + 1} + bx^-n
then x²y” = n(n + 1) y.
Solution:
y = ax^{n + 1} + bx^-n
y_{1 = (n + 1). axⁿ – n bx^-n-1
y2 = n(n + 1). ax^n-1 + n(n + 1) bx^-n-2
∴ x²y2 = n(n + 1) axⁿ⁺¹ + n(n + 1) bx^-n
= n(n + 1) (axn+1+bx_n) = n(n + 1) y
∴ x²y” = n(n + 1) y}

ii) If y = a cos x + (b + 2x) sin x, then y” + y = 4 cos x
Solution:
\(\frac{dy}{dx}\) = y’ = a(-sin x) + (b + 2x) \(\frac{d}{dx}\) (sin x) + sin x \(\frac{d}{dx}\) (b + 2x)
= – a sin x + (b + 2x) cos x + sin x.2
\(\frac{d^{2} y}{d x^{2}}\) = y” = – a cos x + (b + 2x) (- sin x) + cos x (2) + 2 cos x
L.H.S. = y” + y = – a cos x + (b + 2x) (- sin x) + 2 cos x + 2 cos x + a cos x+ (b + 2x) sinx = 4 cosx

iii) If y = 6 (x + 1) + (a + bx) e^3x then y” – 6y’ + 9y = 54 x + 18
Solution:
y’ = 6 \(\frac{d}{dx}\) (x + 1) + (a + bx) \(\frac{d}{dx}\) (e^3x) + e^3x \(\frac{d}{dx}\) (a + bx)
= 6(1) + (a + bx) 3e^3x + e^3x. b.
y” = 0 + 3 (a + bx) \(\frac{d}{dx}\) e^3x + 3e^3x \(\frac{d}{dx}\) (a + bx) + b \(\frac{d}{dx}\) (e^3x)
= 3(a + bx) 3e^3x + 3e^3x(b) + b. 3e^3x
= 9(a + bx) e^3x + 6b e^3x
Now L.H.S. = y” – 6y’ + 9y = 9(a + bx) e^3x + 6be^3x – 6[6 + 3(a + bx)e^3x + be^3x] + 9 [6(x + 1) + (a + bx)e^3x]
= 9(a + bx) e^3x + 6b e^3x – 36 – 18(a + bx)e^3x – 6be^3x + 54x + 54 + 9(a + bx) e^3x = 54x + 18

iv) If ay⁴ = (x + b)⁵ then 5y y” = (y’)²
Solution:
ay⁴ = (x + b)⁵ ; y⁴ = \(\frac{\left(x+b\right)^{2}}{a}\)

v) If y = a cos (sin x) + b sin (sin x) then y” + (tan x) y’ + y cos² x = 0
Solution:
y = a cos (sin x) + b sin (sin x) …………. (1)
Differentiating w.r.to x
y₁ = – a sin (sin x) cos x + b cos (sin x). cos x = [- a sin (sin x) + b cos (sin x)j cos x ………. (2)
Differentiating again w.r.to x.
y₂ = – sin x [-a sin (sin x) + b cos (sin x)] + cos x [- a cos (sin x) cos x – b sin (sin x) cos x]
= – sin x. \(\frac{y_{1}}{\cos x}\) = -cos² x.y
From (1) and (2),
⇒ y₂ + (tan x) y₁ + y cos² x = 0

III.

i) If y = 128 sin³ x cos⁴ x, then find y”.
Solution:
f(x) = 128 sin³ x. cos⁴ x
D.w.r. to x
f'(x)= 128 [sin³ x {4cos³ x (-sinx)} + cos⁴ x {3sin² x. cos x}]
= 128 [3sin² x cos⁵ x – 4sin⁴ x cos³ x]
Again D.w.r to x.
f”(x)= 128 {3 [sin² x 5cos⁴ x . (-sinx) + cos⁵ x. 2sinx cosx] – 4 [sin⁴ x. 3. cos2x (-sinx) + cos³ x. 4 sin³ x. cos x]}
= 128 [-15sin³ x . cos⁴ x + 6sin x cos⁶ x + 12 sin⁵ x cos² x- 16sin³ x cos⁴ x]
f”(x)= 128 [6sinx cos6x + 12sin⁵ x. cos² x – 31sin³ x. cos⁴ x]

ii) If y = sin 2x sin 3x sin 4x, then find y”.
Solution:
f(x) = sin 2x sin 3x sin 4x
= \(\frac{1}{2}\)sin 2x [2sin 4x. sin 3x]
= \(\frac{1}{2}\)sin 2x [cos x – cos 7x]
= \(\frac{1}{2}\) [sin 2x . cos x – cos 7x. sin 2x]
= \(\frac{1}{2}\)×\(\frac{1}{2}\) [2 sin2x. cosx – 2 cos7x. sin2x]
= \(\frac{1}{4}\) [(sin3x + sinx) – (sin9x – sin5x)]
= \(\frac{1}{4}\) [-sin9x + sin5x + sin3x + sinx]
D.w.r. to x
f'(x) = \(\frac{1}{4}\) [-9 cos 9x + 5 cos 5x + 3 cos 3x + cos x]
D.w.r. to x
f”(x) = \(\frac{1}{4}\) [81 sin 9x – 25sin 5x – 9sin 3x – sin x]

iii) If ax² + 2hxy + by² = 1 then prove that
\(\frac{d^{2} y}{d x^{2}}=\frac{h^{2}-a b}{(h x+b y)^{3}}\)
Solution:
Given ax² + 2hxy + by² = 1
Differentiating w.r. to x
a.2x + 2h(x. \(\frac{dy}{dx}\) + y) + b . 2y\(\frac{dy}{dx}\) = 0
2ax + 2hx. \(\frac{dy}{dx}\) + 2hy + 2by. \(\frac{dy}{dx}\) = 0
2(hx + by).\(\frac{dy}{dx}\) = -2(ax + hy)
\(\frac{dy}{dx}\) = \(\frac{-2(ax +hy)}{2(hx+by)}\) = \(\frac{(ax+hy)}{(hx+by)}\) ……… (1)
Differentiating again w.r. to x, \(\frac{d^{2} y}{d x^{2}}\)

iv) If y = ae^-bx cos(cx + d) then prove that y” + 2by’ + (b² + c²) y = 0.
Solution:
Given y = ae^-bx cos(cx + d) ……….. (1)
y₁ = a[e^-bx {- sin (cx + d)}. c. + cos (cx + d) e^-bx (-b)}
= – a. e^-bx [c sin (cx + d) + b cos (cx + d)]
= – ac.e^-bx sin (cx + d) – by
y₁ + by = – ac. e^-bx sin (cx + d) ………. (2)
Differentiating once w.r.to x
y₂ + by₁ = – ac(- b) e^-bx sin (cx + d) – ac e^-bx cos (cx + d) (+ c)
= abce^-bx sin (cx + d) -ac² e^-bx cos (cx + d)
= – b (y₁ + by) c²y [From (1) and (2)]
⇒ y₂ + by₁ + by₁ + b²y + c²y = 0.
⇒ y₂ + 2by₁ + (b² + c²) y = 0 (or)
y” + 2 by’ + (b² + c²) y = 0

v) If y = \(e^{\frac{-k}{2} x}\) (a cos nx + b sin nx) prove that then y” + ky’+ (n² + \(\frac{k^{2}}{4}\))y = 0
Solution:
Given y = \(e^{\frac{-k}{2} x}\) (a cos nx + b sin nx) ………… (1)
∴ y₁ = \(e^{\frac{-k}{2} x}\) (-n. a sin nx + n. b cos nx) + (a cos nx + b sin nx).\(e^{\frac{-k}{2} x}\) (-\(\frac{k}{2}\))
= –\(\frac{k}{2}\) . y – n.e^-kx/2 (a sin nx + b cos nx)
∴ y₁ + \(\frac{k}{2}\) y = – n.e^-kx/2 (a sin nx + b cos nx) …………. (2)
Differentiating w.r. to x k
y₂ + \(\frac{k}{2}\) y₁ = -n[{e^-kx/2 (- na cos nx – nb sin nx)}] + {(a sin nx +b cos nx).e^-kx/2 \(\frac{k}{2}\)}
= – n² e^-kx/2(a cos nx + b sin nx) – \(\frac{k}{2}\){-n.e^-kx/2 (a sin nx + b cos nx)}