Inter 1st Year Maths 1B Differentiation Solutions Ex 9(a)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Differentiation Solutions Exercise 9(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Differentiation Solutions Exercise 9(a)

I. Compute the following limits.

Question 1.
Find the derivatives of the following functions f(x).
i) \(\sqrt{x}+2 x^{\frac{3}{4}}+3 x^{\frac{5}{6}}\) (x > 0)
Solution:
y = \(\sqrt{x}+2 x^{\frac{3}{4}}+3 x^{\frac{5}{6}}\) (x>0)
\(\frac{dy}{dx}\) = \(\frac{1}{2}\).x^-1/2 + 2.\(\frac{3}{4}\).x^-1/4 + 3.\(\frac{5}{6}\).^x-1/6 dx
= \(\frac{1}{2}\)[x^-1/2 + 3.x^-1/4 + 5.x^-1/6]

ii) \(\sqrt{2 x-3}+\sqrt{7-3 x}\).
Solution:

iii) (x² – 3) (4x³ + 1)
Solution:
y = (x² – 3) (4x³ + 1)
\(\frac{dy}{dx}\) = (x² – 3) \(\frac{d}{dx}\) (4x³ + 1) + (4x³ + 1) \(\frac{d}{dx}\)(x² – 3)
= (x² – 3) (12x²) + (4x³ + 1) (2x)
= 12x⁴ – 36x² + 8x⁴ + 2x
= 20x⁴ – 36x² + 2x

iv) (√x – 3x) (x + \(\frac{1}{x}\))
Solution:
y = (√x – 3x) (x + \(\frac{1}{x}\))

v) (√x + 1) (x² – 4x + 2) (x > 0)
Solution:
y = (√x + 1) (x² – 4x + 2) (x > 0)
Differentiating w.r.to x
\(\frac{dy}{dx}\) = (√x + 1) \(\frac{d}{dx}\)(x² – 4x + 2) + (x² – 4x + 2) \(\frac{d}{dx}\)(√x +1)
= (√x + 1) (2x – 4) + \(\frac{x^{2}-4 x+2}{2 \sqrt{x}}\)

vi) (ax + b)ⁿ. (cx + d)^m.
Solution:
y = (ax + b)ⁿ. (cx + d)^m
\(\frac{dy}{dx}\) = (ax + b)ⁿ \(\frac{d}{dx}\)(cx +d)^m + (cx + d)^m \(\frac{d}{dx}\)(ax + b)ⁿ
= (ax + b)ⁿ [m(cx + d)^m-1. c] + (cx + d)^m [n(ax + b)^n-1. a]
= (ax + b)^n-1 (cx + d)^m-1 [cm (ax + b) + an (cx + d)]
= (ax + b)ⁿ (cx + d)^m [\(\frac{an}{ax+b} + \frac{cm}{cx+d}\) ]

vii) 5 sin x + ex log x
Solution:
y = 5 sin x + e^x. log x
\(\frac{dy}{dx}\) = 5 cos x + e^x. \(\frac{d}{dx}\) (log x) + log x \(\frac{d}{dx}\)(e^x)
= 5 cos x + e^x. \(\frac{1}{x}\) + (log x) (e^x)

viii) 5^x + log x + x³ e^x
Solution:
y = 5^x + log x + x³ e^x
\(\frac{dy}{dx}\) = 5^x . log 5 + \(\frac{1}{x}\) + x³.e^x + e^x.3x²
= 5^x. log 5 + – + x³ e^x + 3x² e^x

ix) e^x + sin x cos x
Solution:
y = e^x + sin x . cos x
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) (e^x) + \(\frac{d}{dx}\) (sin x . cos x)
= e^x + sin x \(\frac{d}{dx}\) (cos x) + cos x \(\frac{d}{dx}\) (sin x)
= e^x – sin² x + cos² x
= e^x + cos 2x

x) \(\frac{p x^{2}+e x+r}{a x+b}\)(|a| + |b| ≠ 0)
Solution:

xi) log₇ (log x) (x > 0)
Solution:
y = log₇ (log x) (x > 0)

xii) \(\frac{1}{a x^{2}+b x+c}\) (|a| + |b| + |c| ≠ 0)
Solution:
\(\frac{1}{a x^{2}+b x+c}\) (|a| + |b| + |c| ≠ 0)

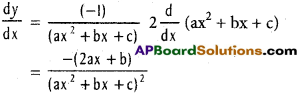
xiii) e^2x log (3x + 4) (x > –\(\frac{4}{3}\))
Solution:
y = e^2x. log (3x + 4) (x > –\(\frac{4}{3}\))
Differentiating w.r.to x
\(\frac{dy}{dx}\) = e^2x \(\frac{d}{dx}\)[log (3x + 4) + log (3x + 4) \(\frac{d}{dx}\) (e^2x)]
= e^2x.\(\frac{1}{3x+4}\) 3 + log (3x + 4). e^2x . 2
= e^2x (\(\frac{3}{3x+4}\) + 2 log (3x + 4))

xiv) (4 + x²) e²xy
Solution:
y = (4 + x²). e^2x
Differentiating w.r.to x
\(\frac{dy}{dx}\) = (4 + x²) \(\frac{d}{dx}\) (e^2x) + e^2x \(\frac{d}{dx}\)(4 + x²)
= (4 + x²). 2e^2x + e^2x (0 + 2x)
= 2e^2x [4 + x² + x]
= 2e^2x (x² + x + 4)

xv) \(\frac{ax+b}{cx+d}\) [|c| + |d|≠0]
Solution:
y = \(\frac{ax+b}{cx+d}\) [|c| + |d|≠0]
Differentiating w.r.to x

xvi) a^x. e^x²
Solution:
y = a^x. e^x²
Differentiating w.r.to x
\(\frac{dy}{dx}\) = (a^x) \(\frac{d}{dx}\)(e^x²) + (e^x²)\(\frac{d}{dx}\)(a^x)
= a^x. e^x². 2x + e^x². a^x. log a
= ax. ^x² (2x + log a)
= y(2x + log a)

Question 2.
If f(x) = 1 + x + x² + + x¹⁰⁰, then find f’ (1).
Solution:
f'(x) = 1 + 2x + 3x² + 100 x⁹⁹
f'(1) = 1+2 + 3 ….+ 100
= \(\frac{100 \times 101}{2}=5050\left(\Sigma x=\frac{x(x+1)}{2}\right)\)

Question 3.
If f (x) = 2x² + 3x – 5, then prove that f(0) + 3f (-1) = 0.
Solution:
f'(x) = 4x + 3
f'(0) = 0 + 3 = 3
f'(-1) = – 4 + 3 = -1
f'(0) + 3f'(-1) = 3 + 3(-1) = 3 – 3 = 0 n.

II.

Question 1.
Find the derivatives of the following functions from the first principles.
i) x³
Solution:


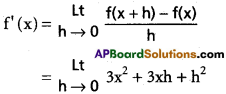
= 3x² + 0 + 0 = 3x²

ii) x⁴ + 4
Solution:
f(x + h) – f(x) = ((x + h)⁴ + 4) – (x⁴ + 4)
= (x + h)4 + 4 – x⁴ – 4 .
= x⁴ + 4x³h + 6x²h² + 4xh³ + h⁴ – x⁴

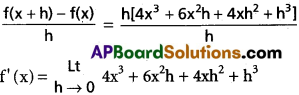
= 4x³ + 0 + 0 + 0 = 4x³

iii) ax² + bx + c
Solution:
f(x + h) = a(x + h)² + b(x + h) + c
= a(x² + 2hx + h²) + b(x + h) + c
= ax² + 2ahx + ah² + bx + bh +c

f(x + h) – f(x) = ax² + 2ahx + ah² + bx + bh + c – ax² – bx – c
= h [2ax + ah + b]

= 2ax + 0 + b = 2ax + b

iv) \(\sqrt{x+1}\)
Solution:

v) sin 2x
Solution:
f(x + h) – f(x) = sin 2(x + h) – sin 2x

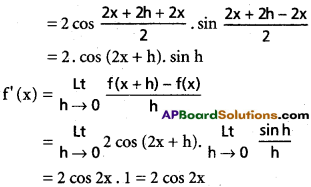
vi) cos ax
Solution:
f(x + h) – f(x) = cos a (x + h) – cos ax

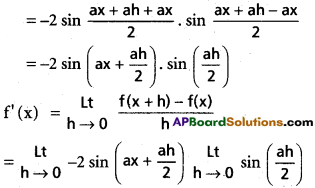
= – 2 sin ax. \(\frac{a}{2}\)
=-a. sin ax

vii) tan 2x
Solution:
f(x + h) – f(x) = tan 2(x + h) – tan 2x

viii) cot x
Solution:
f(x + h) – f(x) = cot (x + h) – cot x

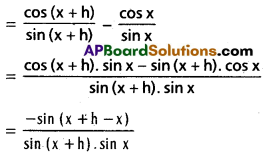
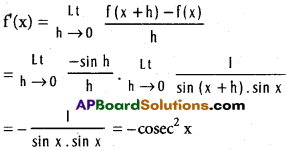
ix) sec 3x
Solution:
f(x + h) – f(x)= sec 3(x + h) – sec 3x

x) x sin x
Solution:
f(x + h) – f(x) = (x + h) sin (x + h) – x sin x
= x (sin (x + h) – sin x) + h. sin (x + h)

xi) cos² x
Solution:
f(x + h) – f(x) = cos² (x + h) – cos² x
= -(cos² x – cos² (x + h))
= -sin (x + h + x) sin (x + h – x)

= -sin 2x. 1 = -sin 2x

Question 2.
Find the derivatives of the following function.
i) \(\frac{1-x \sqrt{x}}{1+x \sqrt{x}}\) (x > 0)
Solution:

ii) xⁿ n^x log (nx) (x > 0, n ∈ N)
Solution:
y = xⁿ. n^x. log nx
\(\frac{dy}{dx}\) = xⁿ. n^x (log nx) + nⁿ. log xn (xⁿ) + xⁿ. log nx (n^x)
= xⁿ. n^x \(\frac{n}{log nx}\) + n^x. log xⁿ (nx^n-1) + xⁿ . log nx. (n^x . log nx)
= x^n-1. n^x[\(\frac{nx}{log nx}\) + log nx. (nⁿ. log nx)]

iii) ax²ⁿ. log x + bxⁿ e^-x
Solution:
y = ax²ⁿ. log x + bxⁿ e^-x
\(\frac{dy}{dx}\) = a (x²ⁿ.\(\frac{1}{x}\) + log x (2nx^2n-1)) + b n (-e^-x) + e^-x. nx^n-1)
= a. x^2n-1 + 2an. x^2n-1. log x – bxⁿ e^-x + bn. x^n-1 . e^-x

iv) (\(\frac{1}{x}\) – x)³ e^x
Solution:
y = (\(\frac{1}{x}\) – x)³ . e^x
\(\frac{dy}{dx}\) = (\(\frac{1}{x}\) – x)³ \(\frac{d}{dx}\)(e^x) + e^x \(\frac{d}{dx}\){(\(\frac{1}{x}\) – x)³}

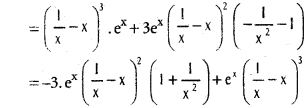
Question 3.
Show that the function f(x) = |x| + |x – 1|, x ∈ R is differentiable for all real numbers except for 0 and 1.
Solution:
f(x) = |x| + |x – 1| ∀ x ∈ R
f(x) = x + x – 1 = 2x – 1, x ≥ 1
= x – (x – 1) = x – x + 1, = 1, 0 < x < 1
= -x – (x – 1) =-x – x + 1 = 1 – 2x, x < 0 ∴ f(x) = 2x – 1, x > 1
= 1, 0 < x < 1 = 1 – 2x, x ≤ 0 If x > 1, then f(x) = 2x – 1 = polynomial in x f(x) is differentiable for all x > 1
If 0 < x < 1, then f(x) = 1 – constant
∴ f(x) is differentiable if 0 < x < 1.
If x < 1, then f(x) = 1 – 2x = polynomial in x.
∴ f(x) is differentiable for all x < 1

Case (i) : x = 0

R f'(0) ≠ Lf'(0)
∴ f'(0) does not exist.
f(x) is not differentiable at x = 0.

Case (ii): x = 1

R f'(1) ≠ L f'(1)
f(1) does not exist.
f(x) is not differentiable at x = 1
∴ f(x) is differentiable for all real x except zero and one.

Question 4.
Verify whether the following function is differentiable at 1 and 3.

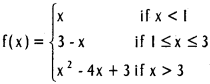
Solution:
Case (i): x = 1

R f'(1) ≠ L f'(1)
f(x) is not differentiable at x = 1

Case (ii) : x = 3

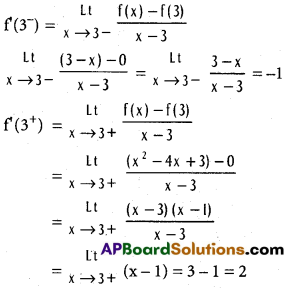
f(3⁺) ≠ f'(3^–)
f(x) is not differentiable at x = 3.

Question 5.
Is the following function f derivable at 2?

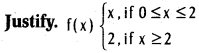
Solution:

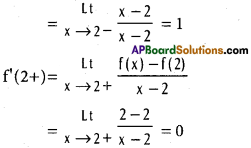
f'(2^–) ≠ f(2⁺); f(x) is not derivable at x = 2.