Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Properties of Triangles Solutions Exercise 10(b) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Properties of Triangles Solutions Exercise 10(b)
All problems in this exercise have reference to ΔABC.
I.
Question 1.
Express \(\Sigma r_{1} \cot \frac{A}{2}\) in terms of s.
Solution:
\(\Sigma r_{1} \cot \frac{A}{2}\) = \(\Sigma\left(s \tan \frac{A}{2}\right) \cot \frac{A}{2}\)
= Σs
= s + s + s
= 3s
Question 2.
Show that Σa cot A = 2(R + r).
Solution:
L.H.S = Σa . cot A
= Σ2R sin A \(\frac{\cos A}{\sin A}\)
= 2R Σ cos A
= \(2 R\left(1+4 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}\right)\) (From transformants)
= \(2\left(R+4 R \sin \frac{A}{2} \cdot \sin \frac{B}{2} \cdot \sin \frac{C}{2}\right)\)
= 2(R + r)
= R.H.S
![]()
Question 3.
In ∆ABC, prove that r1 + r2 + r3 – r = 4R.
Solution:

Question 4.
In ∆ABC, prove that r + r1 + r2 – r3 = 4R cos C.
Solution:


Question 5.
If r + r1 + r2 + r3 then show that C = 90°.
Solution:

II.
Question 1.
Prove that 4(r1r2 + r2r3 + r3r1) = (a + b + c)2
Solution:

Question 2.
Prove that \(\left(\frac{1}{r}-\frac{1}{r_{1}}\right)\left(\frac{1}{r}-\frac{1}{r_{2}}\right)\left(\frac{1}{r}-\frac{1}{r_{3}}\right)=\frac{a b c}{\Delta^{3}}=\frac{4 R}{r^{2} s^{2}}\)
Solution:

Question 3.
Prove that r(r1 + r2 + r3) = ab + bc + ca – s2.
Solution:

Question 4.
Show that \(\sum \frac{r_{1}}{(s-b)(s-c)}=\frac{3}{r}\)
Solution:

![]()
Question 5.
Show that \(\left(r_{1}+r_{2}\right) \tan \frac{C}{2}=\left(r_{3}-r\right) \cot \frac{C}{2}=c\)
Solution:

Question 6.
Show that r1r2r3 = \(r^{3} \cot ^{2} \frac{A}{2} \cdot \cot ^{2} \frac{B}{2} \cdot \cot ^{2} \frac{C}{2}\)
Solution:
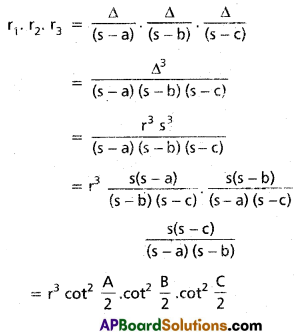
III.
Question 1.
Show that cos A + cos B + cos C = 1 + \(\frac{r}{R}\)
Solution:
L.H.S = cos A + cos B + cos C
= 2 cos(\(\frac{A+B}{2}\)) cos(\(\frac{A-B}{2}\)) + cos C

Question 2.
Show that \(\cos ^{2} \frac{A}{2}+\cos ^{2} \frac{B}{2}+\cos ^{2} \frac{C}{2}=2+\frac{r}{2 R}\)
Solution:
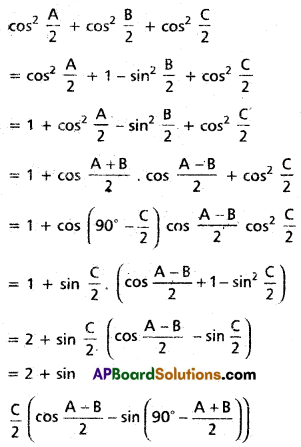

Question 3.
Show that \(\sin ^{2} \frac{A}{2}+\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}=1-\frac{r}{2 R}\)
Solution:
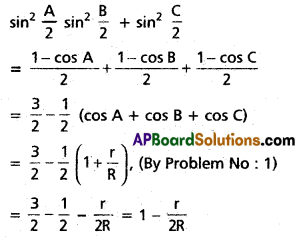
Question 4.
Show that
(i) a = (r2 + r3) \(\sqrt{\frac{r r_{1}}{r_{2} r_{3}}}\)
(ii) ∆ = r1r2 \(\sqrt{\frac{4 R-r_{1}-r_{2}}{r_{1}+r_{2}}}\)
Solution:


![]()
Question 5.
Prove that \(r_{1}^{2}+r_{2}^{2}+r_{3}^{2}+r^{2}\) = 16R2 – (a2 + b2 + c2).
Solution:

Question 6.
If p1, p2, p3 are altitudes drawn from vertices A, B, C to the opposite sides of a triangle respectively, then show that
(i) \(\frac{1}{p_{1}}+\frac{1}{p_{2}}+\frac{1}{p_{3}}=\frac{1}{r}\)
(ii) \(\frac{1}{p_{1}}+\frac{1}{p_{2}}-\frac{1}{p_{3}}=\frac{1}{r_{3}}\)
(iii) p1 . p2 . p3 = \(\frac{(a b c)^{2}}{8 R^{3}}=\frac{8 \Delta^{3}}{a b c}\)
Solution:

Question 7.
If a = 13, b = 14, c = 15, show that R = \(\frac{65}{8}\), r = 4, r1 = \(\frac{21}{2}\), r2 = 12 and r3 = 14.
Solution:
a = 13, b = 14, c = 15
s = \(\frac{a+b+c}{2}\)
= \(\frac{13+14+15}{2}\)
= 21
s – a = 21 – 13 = 8
s – b = 21 – 14 = 7
s – c = 21 – 15 = 6

![]()
Question 8.
If r1 = 2, r2 = 3, r3 = 6 and r = 1, prove that a = 3, b = 4 and c = 5.
Solution:
