AP State Syllabus SSC 10th Class Maths Solutions 6th Lesson Progressions Optional Exercise
AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 6 Progressions Optional Exercise Textbook Questions and Answers.
10th Class Maths 6th Lesson Progressions Optional Exercise Textbook Questions and Answers
Question 1.
Which term of the AP:
121, 117, 113,…, is the first negative term? [Hint: Find n for an < 0]
Answer:
Given A.P: 121, 117, 113, ……
a = 121 and d = a2 – a1
= 117 – 121 = -4
Let the nth term be the first negative term of the given G.P.
Then, an < 0
⇒ an = a + (n – 1) d < 0
⇒ 121 + (n – 1) (-4) < 0
⇒ 121 – 4n + 4 < 0
⇒ 125 – 4n < 0
⇒ -4n < -125
⇒ 4n >125 125
⇒ n > \(\frac{125}{4}\)
n > 31.25
∴ When n = 32, the term becomes negative, (or)
32 nd term is the first negative term of the given A.P.
![]()
Question 2.
The sum of the third and the seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of the AP.
Answer:
Let the 3rd term of AP = a + 2d
and the 7th term of AP = a + 6d
∴ Sum of 3rd and 7th terms = a + 2d + a + 6d = 6
⇒ 2a + 8d = 6
⇒ a + 4d = 3 …… (1)
Now product of above two terms = (a + 2d) (a + 6d) = 8
we can re-write above terms as following
(a + 4d – 2d) (a + 4d + 2d) = 8
⇒ (3 – 2d) (3 + 2d) = 8
⇒ 9 – 4d2 = 8
⇒ 4d2 = 9 – 8 = 1
∴ d2 = \(\frac{1}{4}\)
⇒ d = ± \(\frac{1}{2}\) ……. (2)
Now putting d = \(\frac{1}{2}\) in eq(1) we get
a + 4d = a + 4(\(\frac{1}{2}\)) = 3 ⇒ a = 1
so a = 1, d = \(\frac{1}{2}\)
(or) now putting d = \(\frac{-1}{2}\), we get
a + 4d = a + 4(\(\frac{-1}{2}\)) = 3
⇒ a – 2 = 3
⇒ a = 5
∴ a = 5, d = \(\frac{-1}{2}\)
∴ Sum of sixteen terms =
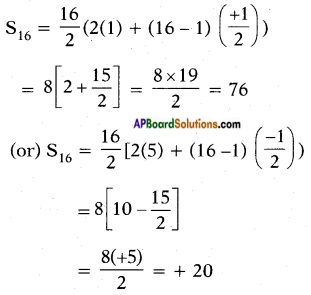
So S16 = 20 or 76
![]()
Question 3.
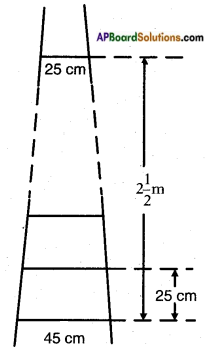
A ladder has rungs 25 cm apart. The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and the bottom rungs are 2\(\frac{1}{2}\) m apart, what is the length of the wood required for the rungs. [Hint: Number of rungs = \(\frac{250}{25}\) + 1]
Answer:
Given: A ladder with rungs separated by a distance of 25 cm.
Total distance between the rungs = 2\(\frac{1}{2}\) m = 250 m
∴ Number of rungs = \(\frac{250}{25}\) + 1 = 10 + 1 = 11
Length of the bottom and top rungs = 45 cm and 25 cm
where a = 45; last term l = a11 = 25 and d = 2 cm
∴ Sn = \(\frac{n}{2}\)(a + l)
= \(\frac{11}{2}\)(45 + 25)
= \(\frac{11}{2}\) × 70
= 35 × 11
= 385 cm
∴ Length of wood required for total rungs = 385 cm.
Question 4.
The houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it. And find this value of x. [Hint: Sx-1 = S49 – Sx]
Answer:
Given: Houses with numbers from 1 to 49.
x is a number x such that,
Sx-1 = S49 – Sx
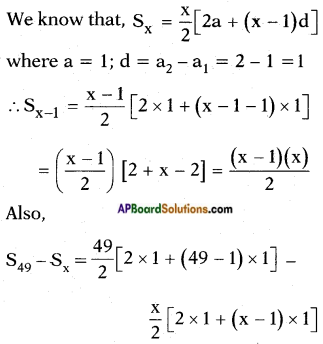

⇒ x(x – 1) + x(x + 1) = 2 × 1225
⇒ x2 – x + x2 + x = 2450
⇒ 2x2 = 2450
⇒ x2 = \(\frac{2450}{2}\) = 1225
⇒ x = √1225 = ±35
∴ x = 35 [∵ x is a counting number]
![]()
Question 5.
A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete.
Each step has a rise of \(\frac{1}{4}\) m and a tread of \(\frac{1}{2}\) m. (see Fig.).
Calculate the total volume of concrete required to build the terrace.
[Hint: Volume of concrete required to build the first step = \(\frac{1}{4}\) × \(\frac{1}{2}\) × 50 m ]

Answer:
Length of each step = 50 m = l
Rise/height of each step = \(\frac{1}{4}\) m = h
Tread of each step = \(\frac{1}{2}\) m = b
Given volume of concrete required to build the first step = \(\frac{1}{4}\) × \(\frac{1}{2}\) × 50 m3 = lbh
We can compare the shape of each step with a cuboid.
Volume of the cuboid = l . b . h
Volumes of concrete required to build the 15 steps are

[∵ 1, 2, 3, 15 is in A.P. where a = 1; d = 1, n = 15]
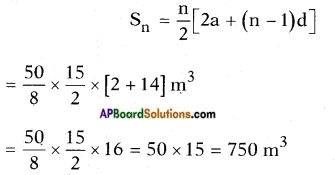
∴ The total volume of concrete required to build the terrace is 750 m3.
![]()
Question 6.
150 workers were engaged to finish a piece of work in a certain number of days. Four workers dropped from the work in the second day. Four workers dropped in third day and so on. It took 8 more days to finish the work. Find the number of days in which the work was completed.
[Let the no.of days to finish the work is ‘x’ then 150x = \(\frac{x+8}{2}\)[2 × 150 + (x + 8 – 1) (-4)]
Answer:
Given: Number of workers engaged initially = 150.
4 workers were dropped each day.
Let the total work was to be completed initially was in x days.
∴ Work done by 150 workers in x days = 150.x.
But due to the dropping of 4 workers each day it took 8 more days.
Work done in this case is
150 × 1 + 146 × 1 + 142 × 1 + …. (x + 8) terms,

= (x + 8) (136 – 2x)
= -2x2 + 136x + 1088 – 16x
= -2x2 + 120x + 1088
∴ 150x = -2x2 + 120x + 1088
⇒ 2x2 + 30x – 1088 = 0
⇒ x2 + 15x – 544 = 0
⇒ x2 + 32x – 17x – 544 =0
⇒ x(x + 32) – 17 (x + 32) = 0
⇒ (x + 32) (x – 17) = 0
⇒ x + 32 = 0 (or) x – 17 = 0
⇒ x = – 32 (or) x = 17
x can’t be negative.
∴ x = 17.
i.e., The total work was completed in x + 8 days = 17 + 8 = 25 days.
![]()
Question 7.
A machine costs Rs. 5,00,000. If the value depreciates 15% in the first year, 13\(\frac{1}{2}\)% in the second year, 12% in the third year and so on. What will be its value at the end of 10 years, when all the percentages will be applied to the original cost?
Answer:
Given: Cost price of a machine = Rs. 5,00,000
Depreciation during the years
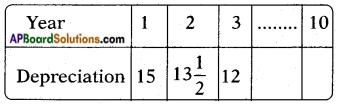
Sum of the depreciations =

∴ Cost after 10 years = (100 – 82.5)% of 5,00,000
= 17.5 % of 5,00,000
= \(\frac{17.5 × 500000}{2}\)
= Rs. 87,500
∴ The value at the end of 10 years will be Rs. 87,500.