AP SSC 10th Class Maths Solutions Chapter 11 Trigonometry Ex 11.2

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 11 Trigonometry Ex 11.2 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Maths Solutions 11th Lesson Trigonometry Exercise 11.2

10th Class Maths 11th Lesson Trigonometry Ex 11.2 Textbook Questions and Answers

Question 1.
Evaluate the following.
i) sin 45° + cos 45°
Answer:
sin 45° + cos 45°
= \(\frac{1}{\sqrt{2}}\) + \(\frac{1}{\sqrt{2}}\)
= \(\frac{1+1}{\sqrt{2}}\)
= \(\frac{2}{\sqrt{2}}\)
= \(\frac{\sqrt{2} \times \sqrt{2}}{\sqrt{2}}\)
= √2

ii)

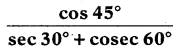
Answer:

iii)

Answer:

iv) 2 tan² 45° + cos² 30° – sin² 60°
Answer:
2 tan² 45° + cos² 30° – sin² 60°
= 2(1)² + \(\left(\frac{\sqrt{3}}{2}\right)^{2}\) – \(\left(\frac{\sqrt{3}}{2}\right)^{2}\)
= \(\frac{2}{1}\) + \(\frac{3}{4}\) – \(\frac{3}{4}\)
= \(\frac{8+3-3}{4}\)
= \(\frac{8}{4}\)
= 2

v)

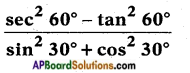
Answer:

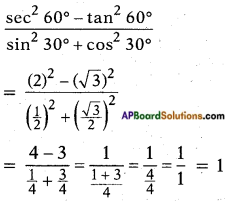
Question 2.
Choose the right option and justify your choice.
i) \(\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 45^{\circ}}\)
a) sin 60°
b) cos 60°
c) tan 30°
d) sin 30°
Answer:

ii) \(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}\)
a) tan 90°
b) 1
c) sin 45°
d) 0
Answer:
\(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}\) = \(\frac{1-(1)^{2}}{1+(1)^{2}}\)
= \(\frac{0}{1+1}\) = \(\frac{0}{2}\) = 0

iii) \(\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}\)
a) cos 60°
b) sin 60°
c) tan 60°
d) sin 30°
Answer:

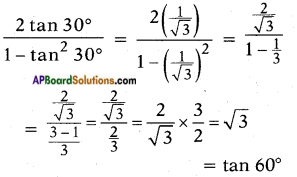
Question 3.
Evaluate sin 60° cos 30° + sin 30° cos 60°. What is the value of sin (60° + 30°). What can you conclude?
Answer:
Take sin 60°.cos 30° + sin 30°.cos 60°
= \(\frac{\sqrt{3}}{2}\) . \(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2}\) . \(\frac{1}{2}\)
= \(\frac{(\sqrt{3})^{2}}{4}\) + \(\frac{1}{4}\)
= \(\frac{3}{4}\) + \(\frac{1}{4}\)
= \(\frac{3+1}{4}\)
= \(\frac{4}{4}\) = 1 …… (1)
Now take sin (60° + 30°)
= sin 90° = 1 …….. (2)
From equations (1) and (2), I conclude that
sin (60°+30°) = sin 60° . cos 30° + sin 30° . cos 60°.
i.e., sin (A + B) = sin A . cos B + cos A . sin B

Question 4.
Is it right to say cos (60° + 30°) = cos 60° cos 30° – sin 60° sin 30° ?
Answer:
L.H.S. = cos (60° + 30°)
cos 90° = 0
R.H.S. = cos 60° . cos 30° – sin 60° . sin 30°.
= \(\frac{1}{2}\) . \(\frac{\sqrt{3}}{2}\) – \(\frac{\sqrt{3}}{2}\) . \(\frac{1}{2}\)
= \(\frac{\sqrt{3}}{4}\) – \(\frac{\sqrt{3}}{4}\) = 0
∴ L.H.S = R.H.S
Yes, it is right to say
cos (60°+30°) = cos 60° . cos 30° – sin 60° . sin 30°.
i.e., cos (A + B) = cos A . cos B – sin A . sin B

Question 5.
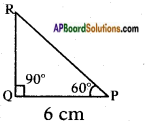
In right angle triangle △PQR, right angle is at Q and PQ = 6 cms, ∠RPQ = 60°. Determine the lengths of QR and PR.
Answer:
Given that △PQR is a right angled triangle, right angle is at Q and PQ = 6 cm, ∠RPQ = 60°.

tan 60° = \(\frac{\text { Opposite side to } \angle P}{\text { Adjacent side to } \angle P}\)
√3 = \(\frac{RQ}{6}\)
which gives RQ = 6√3 cm ……. (1)
To find the length of the side RQ, we consider

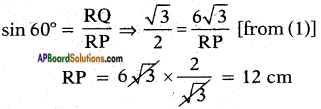
∴ The length of QR is 6√3 and RP is 12 cm.

Question 6.
In △XYZ, right angle is at Y, YZ = x, and XY = 2x then determine ∠YXZ and ∠YZX.
Answer:
Note: In the problem take
YX = x, and XZ = 2x.

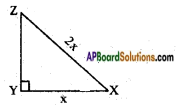
Given that △XYZ is a right angled triangle and right angle at Y, and YX = x and XZ = 2x.
By Pythagoras theorem
XZ² = XY² + YZ²
(2x)² = (x)² + YZ²
4x² = x² + YZ²
YZ² = 4x² – x² = 3x²
YZ = \(\sqrt{3 x^{2}}\) = √3x
Now, from the △XYZ
tan X = \(\frac{XZ}{XY}\) = \(\frac{\sqrt{3} x}{x}\)
tan X = √3 = tan 60°
∴ Angle YXZ is 60°.
tan Z = \(\frac{XY}{YZ}\) = \(\frac{x}{\sqrt{3} x}\)
tan Z = \(\frac{1}{\sqrt{3}}\) = tan 30°
∴ Angle YZX is 30°.
Hence ∠YXZ and ∠YZX are 60° and 30°.

Question 7.
Is it right to say that
sin (A + B) = sin A + sin B? Justify your answer.
Answer:
Let A = 30° and B = 60°
L.H.S = sin (A + B)
= sin (30° + 60°) = sin 90° = 1
R.H.S = sin 30° + sin 60°
= \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\)
= \(\frac{\sqrt{3}+1}{2}\)
Hence L.H.S ≠ R.H.S
So, it is not right to say that sin (A + B) = sin A + sin B