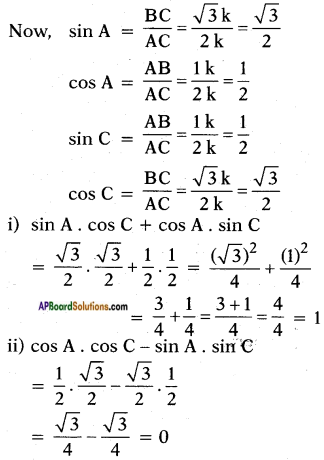AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 11 Trigonometry Ex 11.1 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 11th Lesson Trigonometry Exercise 11.1
10th Class Maths 11th Lesson Trigonometry Ex 11.1 Textbook Questions and Answers
Question 1.
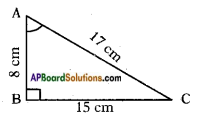
In right angle triangle ABC, 8 cm, 15 cm and 17 cm are the lengths of AB, BC and CA respectively. Then, find out sin A, cos A and tan A.
Answer:
Given that
△ABC is a right angle triangle and Lengths of AB, BC and CA are 8 cm, 15 cm and 17 cm respectively.
Among the given lengths CA is longest.
Hence CA is the hypotenuse in △ABC and its opposite vertex having right angle.
i.e., ∠B = 90°.
With reference to ∠A, we have opposite side = BC = 15 cm
adjacent side = AB = 8 cm
and hypotenuse = AC = 17
sin A = \(\frac{\text { Opposite side of } \angle \mathrm{A}}{\text { Hypotenuse }}\) = \(\frac{BC}{AC}\) = \(\frac{15}{17}\)
cos A = \(\frac{\text { Adjacent side of } \angle \mathrm{A}}{\text { Hypotenuse }}\) = \(\frac{AB}{AC}\) = \(\frac{8}{17}\)
tan A = \(\frac{\text { Opposite side of } \angle \mathrm{A}}{\text { Adjacent side of } \angle \mathrm{A}}\) = \(\frac{BC}{AB}\) = \(\frac{15}{8}\)
∴ sin A = \(\frac{15}{17}\);
cos A = \(\frac{8}{17}\)
tan A = \(\frac{15}{8}\)
![]()
Question 2.
The sides of a right angle triangle PQR are PQ = 7 cm, QR = 25 cm and ∠P = 90° respectively. Then find, tan Q – tan R.
Answer:
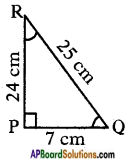
Given that △PQR is a right angled triangle and PQ = 7 cm, QR = 25 cm.
By Pythagoras theorem QR2 = PQ2 + PR2
(25)2 = (7)2 + PR2
PR2 = (25)2 – (7)2 = 625 – 49 = 576
PR = √576 = 24 cm
tan Q = \(\frac{PR}{PQ}\) = \(\frac{24}{7}\);
tan R = \(\frac{PQ}{PR}\) = \(\frac{7}{24}\)
∴ tan Q – tan R = \(\frac{24}{7}\) – \(\frac{7}{24}\)
= \(\frac{(24)^{2}-(7)^{2}}{168}\)
= \(\frac{576-49}{168}\)
= \(\frac{527}{168}\)
Question 3.
In a right angle triangle ABC with right angle at B, in which a = 24 units, b = 25 units and ∠BAC = θ. Then, find cos θ and tan θ.
Answer:
Given that ABC is a right angle triangle with right angle at B, and BC = a = 24 units, CA = b = 25 units and ∠BAC = θ.
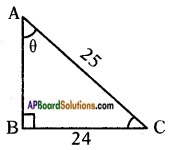
By Pythagoras theorem
AC2 = AB2 + BC2
(25)2 = AB2 + (24)2
AB2 = 252 – 242 = 625 – 576
AB2 = 49
AB = √49 = 1
With reference to ∠BAC = θ, we have
Opposite side to θ = BC = 24 units.
Adjacent side to θ = AB = 7 units.
Hypotenuse = AC = 25 units.
Now
cos θ = \(\frac{\text { Adjacent side of } \theta}{\text { Hypotenuse }}\) = \(\frac{AB}{AC}\) = \(\frac{7}{25}\)
tan θ = \(\frac{\text { Opposite side of } \theta}{\text { Adjacent side of } \theta}\) = \(\frac{BC}{AB}\) = \(\frac{24}{7}\)
Hence cos θ = \(\frac{7}{25}\) and tan θ = \(\frac{24}{7}\)
![]()
Question 4.
If cos A = \(\frac{12}{13}\), then find sin A and tan A.
Answer:
From the identity
sin2 A + cos2 A = 1
⇒ sin2 A = 1 – cos2 A
= 1 – \(\left(\frac{12}{13}\right)^{2}\)
= 1 – \(\frac{144}{169}\)
= \(\frac{169-144}{169}\)
= \(\frac{25}{169}\)
∴ sin A = \(\sqrt{\frac{25}{169}}\) = \(\frac{5}{13}\)
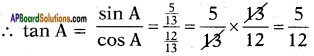
∴ sin A = \(\frac{5}{13}\); tan A = \(\frac{5}{12}\)
Question 5.
If 3 tan A = 4, then find sin A and cos A.
Answer:
Given 3 tan A = 4
⇒ tan A = \(\frac{4}{3}\)
From the identify sec2 A – tan2 A = 1
⇒ 1 + tan2 A = sec2 A
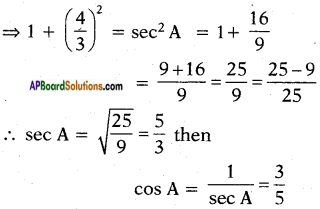
If cos A = \(\frac{3}{5}\) then from
sin2 A + cos2 A = 1
We can write sin2A = 1 – cos2A
= 1 – \(\left(\frac{3}{5}\right)^{2}\)
= 1 – \(\frac{9}{25}\)
⇒ sin2 A = \(\frac{16}{25}\)
⇒ sin A = \(\frac{4}{5}\)
∴ sin A = \(\frac{4}{5}\); cos A = \(\frac{3}{5}\)
![]()
Question 6.
In △ABC and △XYZ, if ∠A and ∠X are acute angles such that cos A = cos X then show that ∠A = ∠X.
Answer:
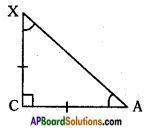
In the given triangle, cos A = cos X
⇒ \(\frac{AC}{AX}\) = \(\frac{XC}{AX}\)
⇒ AC = XC
⇒ ∠A = ∠X (∵ Angles opposite to equal sides are also equal)
Question 7.
Given cot θ = \(\frac{7}{8}\), then evaluate

Answer:
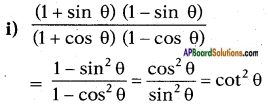
cot2 θ = (cot θ)2
= \(\left(\frac{7}{8}\right)^{2}\) = \(\frac{49}{64}\) …… (1)
![]()
= sec θ + tan θ
So cot θ = \(\frac{7}{8}\)
⇒ tan θ = \(\frac{8}{7}\)
⇒ tan2 θ = \(\left(\frac{8}{7}\right)^{2}\) = \(\frac{64}{49}\)
From sec2 θ – tan2 θ = 1
⇒ 1 + tan2 θ = sec2 θ

![]()
Question 8.
In a right angle triangle ABC, right angle is at B, if tan A = √3, then find the value of
i) sin A cos C + cos A sin C
ii) cos A cos C – sin A sin C
Answer:
Given, tan A = \(\frac{\sqrt{3}}{1}\)
Hence \(\frac{\text { Opposite side }}{\text { Adjacent side }}=\frac{\sqrt{3}}{1}\)
Let opposite side = √3k and adjacent side = 1k
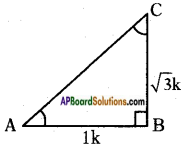
In right angled △ABC,
AC2 = AB2 + BC2
(By Pythagoras theorem)
⇒ AC2 = (1k)2 + (√3k)2
⇒ AC2 = 1k2 + 3k2
⇒ AC2 = 4k2
∴ AC = \(\sqrt{4 k^{2}}\) = 2k