AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 1 Real Numbers Ex 1.3 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.3
10th Class Maths 1st Lesson Real Numbers Ex 1.3 Textbook Questions
Question 1.
Write the following rational numbers in their decimal form and also state which are terminating and which have non-terminating repeating decimals.
i) \(\frac{3}{8}\)
ii) \(\frac{229}{400}\)
iii) 4\(\frac{1}{5}\)
iv) \(\frac{2}{11}\)
v) \(\frac{8}{125}\)
Answer:
i) \(\frac{3}{8}\)

[!! Denominator 8 = 23, consists of only 2’s. Hence a terminating decimal.]
∴ \(\frac{3}{8}\) = 0.375 is a terminating decimal.
![]()
ii) \(\frac{229}{400}\)

[!! Denominator 400 = 24 × 52 = 2n × 5m. Hence a terminating decimal.]
∴ \(\frac{229}{400}\) = 0.5725 is a terminating decimal.
iii) 4\(\frac{1}{5}\)
4\(\frac{1}{5}\) = 4 + \(\frac{1}{5}\)
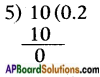
[!! Denominator is 5. Hence a terminating decimal.]
∴ 4\(\frac{1}{5}\) = 4.2 is a terminating decimal.
iv) \(\frac{2}{11}\)
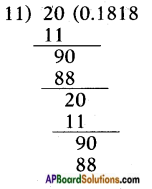
[!! Denominator is not of the form 2m × 5n. Hence a non-terminating repeating decimal.]
∴ \(\frac{2}{11}\) = \(0 . \overline{18}\) is a non terminating, repeating decimal.
![]()
v) \(\frac{8}{125}\)

[!! Denominator 125 = 53. Hence a terminating decimal.]
∴ \(\frac{8}{125}\) = 0.064 is a terminating decimal.
Question 2.
Without performing division, state whether the following rational numbers will have a terminating decimal form or a non-terminating, repeating decimal form.
i) \(\frac{13}{3125}\)
ii) \(\frac{11}{12}\)
iii) \(\frac{64}{455}\)
iv) \(\frac{15}{1600}\)
v) \(\frac{29}{343}\)
vi) \(\frac{23}{2^{3} \cdot 5^{2}}\)
vii) \(\frac{129}{2^{2} \cdot 5^{7} \cdot 7^{5}}\)
viii) \(\frac{9}{15}\)
iX) \(\frac{36}{100}\)
X) \(\frac{77}{210}\)
Answer:
i) \(\frac{13}{3125}\)
Note: We check whether the denominator is of the form 2n . 5m or not? If yes, the rational number can be expressed as a terminating decimal. If not, it can’t be expressed as a terminating decimal.
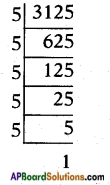
[!! Denominator is of the form 2m × 5n. Hence a terminating decimal.]
3125 = 55
∴ \(\frac{13}{3125}\) is a terminating decimal.
ii) \(\frac{11}{12}\)
The denominator 12 is not a factor of 11. Moreover 12 = 22 × 3.
[!! Denominator is not of the form 2m × 5n.]
∴ \(\frac{11}{12}\) is a non terminating, repeating decimal.
![]()
iii) \(\frac{64}{455}\)

[!! Denominator is not of the form 2m × 5n. Hence a non terminating decimal.]
∴ 455 = 5 × 7 × 13
Hence\(\frac{64}{455}\) is a non terminating, repeating decimal.
iv) \(\frac{15}{1600}\)

∴ 1600 = 26 × 52 [∵ The denominator is of the form 2n . 5m]
Hence \(\frac{15}{1600}\) is a terminating decimal.
v) \(\frac{29}{343}\)
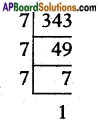
343 = 73 [Not of the form 2n . 5m]
∴ \(\frac{29}{343}\) is a non terminating, repeating decimal.
vi) \(\frac{23}{2^{3} \cdot 5^{2}}\)
\(\frac{23}{2^{3} \cdot 5^{2}}\) is a terminating decimal.
[∵ The denominator is of the form 2n . 5m]
vii) \(\frac{129}{2^{2} \cdot 5^{7} \cdot 7^{5}}\)
\(\frac{129}{2^{2} \cdot 5^{7} \cdot 7^{5}}\) is a non terminating, repeating decimal.
viii) \(\frac{9}{15}\)
\(\frac{9}{15}\) = \(\frac{3}{5}\)
Denominator is of the form 2n . 5m.
∴ \(\frac{9}{15}\) = \(\frac{3}{5}\) is a terminating decimal.
ix) \(\frac{36}{100}\)
100 = 22 × 52 is of the form 2n . 5m
Hence \(\frac{36}{100}\) is a terminating decimal.
![]()
x) \(\frac{77}{210}\)
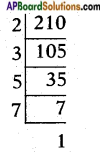
210 = 2 × 3 × 5 × 7 is not of the form 2n . 5m
Given fraction has a non-terminating, repeating decimal expansion.
Question 3.
Write the following rationals in decimal form using Theorem 1.4.
i) \(\frac{13}{25}\)
ii) \(\frac{15}{16}\)
iii) \(\frac{23}{2^{3} \cdot 5^{2}}\)
iv) \(\frac{7218}{3^{2} \cdot 5^{2}}\)
v) \(\frac{143}{110}\)
Answer:
i) \(\frac{13}{25}\)

ii) \(\frac{15}{16}\)
\(\frac{15}{16}\) = \(\frac{15}{2 \times 2 \times 2 \times 2}\)

iii) \(\frac{23}{2^{3} \cdot 5^{2}}\)
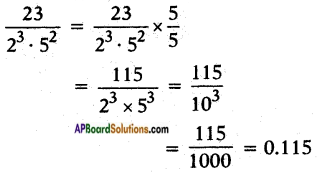
![]()
iv) \(\frac{7218}{3^{2} \cdot 5^{2}}\)
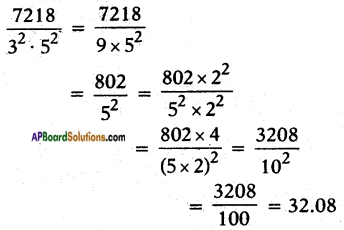
v) \(\frac{143}{110}\)
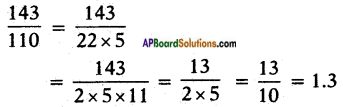
Question 4.
The decimal form of some real numbers are given below. In each case, decide whether the number is rational or not. If it is rational, and expressed in form p/q, what can you say about the prime factors of q?
i) 43.12345678?
ii) 0.120120012000120000 ……….
iii) \(43 . \overline{123456789}\)
Answer:
i) 43.123456789
The given decimal expansion is terminating. Hence it is a rational number and the denominator q is of the form 2n . 5m.
![]()
ii) 0.120120012000120000 …………
The given decimal expansion is neither terminating nor repeating.
Hence it is not a rational number. It represents an irrational number.
iii) \(43 . \overline{123456789}\)
The given real number is a repeating decimal with period 123456789. Hence it is a rational number.