AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 1 Real Numbers Ex 1.2 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.2
10th Class Maths 1st Lesson Real Numbers Ex 1.2 Textbook Questions and Answers
Question 1.
Express each of the following numbers as a product of its prime factors.
i) 140
ii) 156
iii) 3825
iv) 5005
v) 7429
Answer:
i) 140
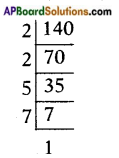
∴ 140 = 2 × 2 × 5 × 7 = 22 × 5 × 7
![]()
ii) 156
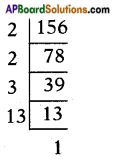
∴ 156 = 2 × 2 × 3 × 13 = 22 × 3 × 13
iii) 3825

∴ 3825 = 3 × 3 × 5 × 5 × 17 = 32 × 52 × 17
iv) 5005
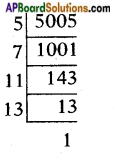
∴ 5005 = 5 × 7 × 11 × 13
v) 7429

∴ 7429 = 17 × 19 × 23
![]()
Question 2.
Find the L.C.M and H.C.F of the following integers by the prime factorization method.
i) 12, 15 and 21
ii) 17, 23 and 29
iii) 8, 9 and 25
iv) 72 and 108
v) 306 and 657
Answer:
i) 12, 15 and 21
12 = 2 × 2 × 3 = 22 × 3
15 = 3 × 5
21 = 3 × 7
L.C.M = 22 × 3 × 5 × 7 = 420
H.C.F = 3
ii) 17, 23 and 29
The given numbers 17, 23 and 29 are all primes.
L.C.M = their product
= 17 × 23 × 29 = 11339
∴ H.C.F = 1
iii) 8, 9 and 25
8 = 2 × 2 × 2 = 23
9 = 3 × 3 = 32
25 = 5 × 5 = 52
L.C.M = 23 × 32 × 52 = 1800
(or)
8, 9 and 25 are relatively prime, therefore L.C.M is equal to their product,
(i.e.,) L.C.M = 8 × 9 × 25 = 1800
H.C.F = 1
iv) 72 and 108
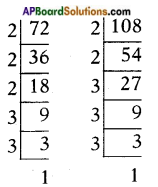
72 = 23 × 32
108 = 22 × 33
L.C.M = 23 × 33 = 8 × 27 = 216
H.C.F = 22 × 32 = 4 × 9 = 36
![]()
v) 306 and 657
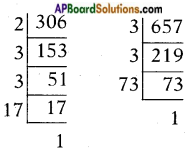
306 = 2 × 32 × 17
657 = 32 × 73
L.C.M = 2 × 32 × 17 × 73 = 22338
H.C.F = 32 = 9
Question 3.
Check whether 6n can end with the digit ‘0’ for any natural number n.
Answer:
Given number = 6n = (2 × 3)n
The prime factors here are 2 and 3 only.
To be end with 0; 6n should have a prime factor 5 and also 2.
So, 6n can’t end with zero.
Question 4.
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
Answer:
Given numbers are 7 × 11 × 13
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
⇒ 13(7 × 11 + 1) and
5(7 × 6 × 4 × 3 × 2 × 1 + 1)
⇒ 13 K and 5 L, where K = 78 and L = 7 × 6 × 4 × 3 × 2 × 1 + 1 = 1009
As the given numbers can be written as product of two numbers, they are composite.
Question 5.
How will you show that (17 × 11 × 2) + (17 × 11 × 5) is a composite number? Explain.
Answer:
(17 × 11 × 2) + (17 × 11 × 5)
= (17 × 11) (2 + 5)
= (17 × 11) (7)
= 187 × 7
Now the given expression is written as a product of two integers and hence it is a composite number.
![]()
Question 6.
What is the last digit of 6100?
Answer: We know that
61 = 6
62 = 36
63 = 216
64 = 1296
65 = 7776
We see that 6n for any positive integer n ends is 6.
i.e., unit digit is always 6.
∴ Unit digit of 6100 is 6.