AP SSC 10th Class Maths Notes Chapter 9 Tangents and Secants to a Circle

Students can go through AP SSC 10th Class Maths Notes Chapter 9 Tangents and Secants to a Circle to understand and remember the concepts easily.

AP State Syllabus SSC 10th Class Maths Notes Chapter 9 Tangents and Secants to a Circle

→ The locus of points which are joined by a curve and are equidistant from a fixed point is called a circle. The fixed point here is called the centre of the circle.
(or)
A simple closed curve consisting of all points in a plane which are equidistant from a fixed point is called a circle. The fixed point is its centre and the fixed distance is its radius.

→ The path followed by a circular object is a straight line.

→ The line segment joining any two points on a circle is called a ‘chord’. The longest of all chords of a circle passes through the centre and is called a diameter.

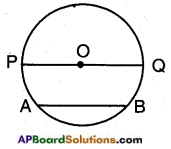
\(\overline{\mathrm{AB}}\) is a chord and \(\overline{\mathrm{PQ}}\) is a diameter.
\(\overline{\mathrm{OP}}\) is the radius of the circle,
diameter = 2 × radius d = 2r
r = \(\frac{d}{2}\)

→ There are three different possibilities for a given line and a circle.

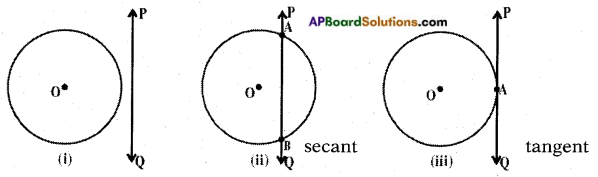
Case (i): The line PQ and the circle have no point in common (or) they do not touch each other.
Case (ii): The line PQ and the circle have two common points (or)
The line PQ intersects the circle at two distinct points A and B. Here the line PQ is a “secant” of the circle.
Case (iii): The line PQ touches the circle at an unique point A (or) there is one and only one point common to both the line and circle.
Here \(\stackrel{\leftrightarrow}{\mathrm{PQ}}\) is called a tangent to the circle at ‘A’.

→ The word tangent is derived from the Latin word “TANGERE” which means “to touch” and was introduced by Danish mathematician“Thomas Fineke” in 1583.

→ There is only one tangent to the circle at one point.

→ The tangent at any point of a circle is perpendicular to the radius through the point of contact.

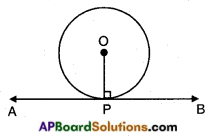
The radius OP is perpendicular to \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) at P.
i.e, OP ⊥ AB.

→ Construction of a tangent to a circle:
Draw a circle with centre ‘O’.
Take a point ‘P’ on it. Join OP.
Draw a perpendicular line to OP through ‘P’.

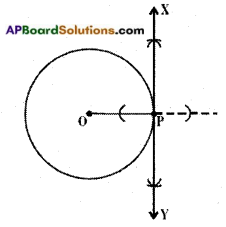
Let it be \(\stackrel{\leftrightarrow}{\mathrm{XY}}\)
XY is the required tangent to the given circle passing through P.

→ Let ‘O’ be the centre of the given circle and \(\overline{\mathrm{AP}}\) is a tangent through A where OA is the radius, then the length of the tangent AP = \(\sqrt{\mathrm{OP}^{2}-\mathrm{OA}^{2}}\).

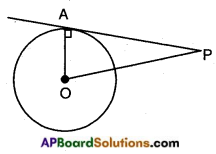
→ Two tangents can be drawn to a circle from an external point.

→ Let ‘O’ be the centre of the circle and P is an exterior point. There are exactly two tangents to the circle through P.
\(\overline{\mathrm{PA}}\) and \(\overline{\mathrm{PB}}\) are the tangents.

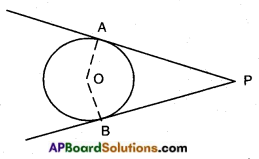
Here the lengths of the two tangents drawn from the external points are equal.
\(\overline{\mathrm{PA}}\) = \(\overline{\mathrm{PB}}\)

→ Construction of tangents to a circle from an external point:
Step – 1: Draw a circle with centre ‘O’ and with given radius.
Step – 2: Mark a point ‘P’ in the exterior of the circle and join ‘OP’.
Step – 3: Draw the perpendicular bisector \(\stackrel{\leftrightarrow}{\mathrm{XY}}\) to \(\overline{\mathrm{OP}}\), intersecting at M.
Step – 4: Taking M as centre, MP or OM as radius, draw a circle which intersects the given circle at A and B.

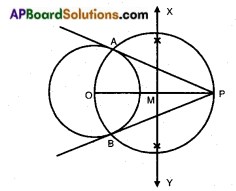
Step – 5: Join PA and PB. PA and PB are the required tangents.

→ Consider a circle with centre ‘O’. PA and PB are the tangents from an exterior point ‘P’. Then, the centre of the circle lies on the bisector of the angle between two tangents drawn from the exterior point P.
∠OPA = ∠OPB

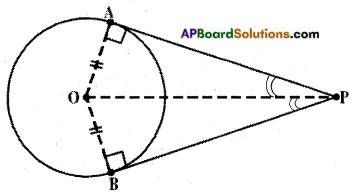
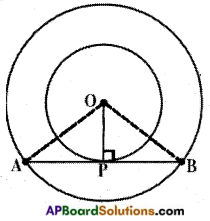
→ Consider two concentric circles with centre ‘O’. Let the chord \(\overline{\mathrm{AB}}\) of the larger/ bigger circle just touches the smaller circle, then it is bisected at the point of contact with the smaller circle.
In the figure, \(\overline{\mathrm{AB}}\) is the chord of bigger circle touching the smaller circle at P then AP = PB.

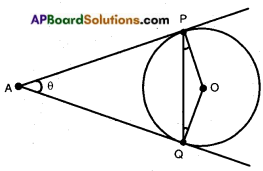
→ If AP and AQ are two tangents to a circle with centre ‘O’, then ∠PAQ = 2∠OPQ = 2∠OQP.

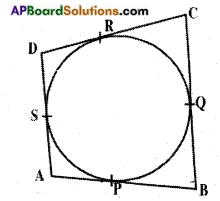
→ If a circle touches the sides of a quadrilateral ABCD at points P, Q, R and S then AB + CD = BC + DA.
i.e., sum of the opposite sides are equal.

→ The region enclosed by a secant/chord and an arc is called a ‘segment of the circle’.

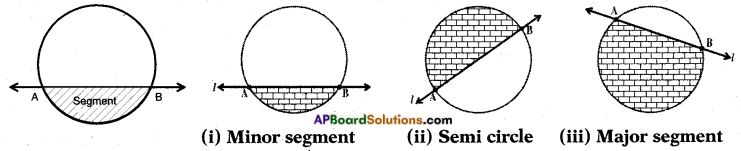
Case (i): If the arc is a minor arc then the segment is a minor segment.
Case (ii): If the arc is a semi arc then the segment is a semi circle.
Case (iii): If the arc is a major arc then the segment is a major segment.

→ Area of a segment between the chord AB and whose arc makes an angle ‘x’ at the centre = \(\frac{x}{360}\) × πr²

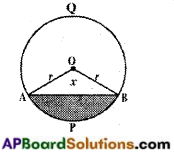
i.e., Area of the segment APB = (Area of the corresponding sector OAPB) – (Area of the corresponding triangle OAB).