Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 14th Lesson Kinetic Theory Textbook Questions and Answers.
AP Inter 1st Year Physics Study Material 14th Lesson Kinetic Theory
Very Short Answer Questions
Question 1.
Define mean free path. [A.P. Mar. 18, 17, 15; T.S. Mar. 17, 15]
Answer:
The average distance covered by a molecule between two successive collisions is called the mean free path.
Question 2.
How does kinetic theory justify Avogadro’s hypothesis and show that Avogadro Number in different gases is same ?
Answer:
For two different gases, we have \(\frac{P_1 V_1}{N_1 T_1}=\frac{P_2 V_2}{N_2 T_2}\) = KB (constant)
If P, V, T are same, then N is also same for two gases.
N is called Avogadro’s number. According to Avogadro’s hypothesis, that the number of molecules per unit volume is same for all gases at a fixed temperature and pressure.
In this way kinetic theory justify Avogadro’s hypothesis.
![]()
Question 3.
When does a real gas behave like an ideal gas ? [T.S. Mar. 16; Mar. 14]
Answer:
At low pressures and high temperatures real gases behave like an ideal gas.
Question 4.
State Boyle’s Law and Charle’s Law. [A.P. Mar. 18; T.S. Mar. 15]
Answer:
Boyle’s law : At constant temperature, the pressure of a given mass of gas varies inversely with volume.
Charle’s law: At constant pressure, the volume of the gas is proportional to its absolute temperature.
Question 5.
State Dalton’s law of partial pressures. [T.S. Mar. 18; A.P. Mar. 16; Mar. 14]
Answer:
The total pressure exerted by a mixture of non-reacting gases occupying a vessel is equal to the sum of the individual pressures which each gas would exert if it is alone occupied the whole vessel.
i.e., P = P1 + P2 + ………….
Question 6.
Pressure of an ideal gas in container is independent of shape of the container – explain. [T.S. Mar. 17]
Answer:
The kinetic theory expression for the pressure of a given mass of an ideal gas in a container is 1 -2.
P = \(\frac{1}{3}\) nm\(\bar{v}^2\), where \(\overline{\mathrm{V}}\) indicates mean-square-speed, n is number of molecules, m is mass of molecule. From the above equation, shape of the container is immeterial. Hence pressure of an ideal gas is independent of shape of the container.
![]()
Question 7.
Explain the concept of degrees of freedom for molecules of a gas.
Answer:
The degrees of freedom of a particle indicate the number of independent motions which the particle can undergo, or the number of independent methods of exchanging energy.
A monoatomic molecule (He) has three degrees of freedom, a diatomic (H2, O2) one has five, while a triatomic (H2O) one has six.
Question 8.
What is the expression between pressure and kinetic energy of a gas molecules ? [AP – Mar. ’17, ’16, ’15]
Answer:
By kinetic theory pressure, P = \(\frac{1}{3} m n \overline{V}^2\) and kinetic energy = \(\frac{1}{2} m n \overline{V}^2\) where m is the mass of the molecules, n is the number of moles per unit volume, v is the mean-square-speed.
∴ P = \(\frac{2}{3}\left(\frac{1}{2} m n \overline{V}^2\right)\) = \(\frac{2}{3}\) (kineticenergy)
Question 9.
The absolute temperature of a gas is increased 3 times. What will be the increase in rms velocity of the gas molecule ?
Answer:
Case (i) : The r.m.s velocity of gas molecule, \(\overline{V}_1=\sqrt{\frac{3 R T_1}{M}}\)
Case (ii) : The r.m.s velocity of gas molecule, \(\overline{V}_2=\sqrt{\frac{3 R T_2}{M}}\)
\(\frac{\overline{\mathrm{V}}_2}{\overline{\mathrm{V}}_1}=\sqrt{\frac{\mathrm{T}_2}{\mathrm{~T}_1}}=\sqrt{\frac{3 \mathrm{~T}_1}{\mathrm{~T}_1}}\) [∵ T2 = 3T1] ⇒ \(\overline{\mathrm{V}}_2=\sqrt{3} \overline{\mathrm{V}}_1=1.732 \overline{\mathrm{V}}_1\)
∴ Increase in r.m.s velocity of gas molecule = \(\overline{\mathrm{V}}_2-\overline{\mathrm{V}}_1=1.732 \overline{\mathrm{V}}_1-\overline{\mathrm{V}}_1=0.732 \overline{\mathrm{V}}_1\)
Short Answer Questions
Question 1.
Explain the kinetic interpretation of Temperature.
Answer:
Kinetic interpretation of Temperature : Since the pressure of the gas is given by
P = \(\frac{1}{3} \mathrm{mn} \overline{\mathrm{V}}^2\), where m = mass of the gas, n = \(\frac{\mathrm{N}}{\mathrm{V}}\) = Number of molecules per unit volume
\(\overline{V}\) = r.m.s velocity of gas, P = \(\frac{1}{3} m \frac{N}{V} \overline{V}^2\) ⇒ PV = \(\frac{1}{3} \mathrm{mN} \overline{\mathrm{V}}^2\)
Also for a gram molecule of the gas, PV = RT
Hence RT = \(\frac{1}{3} m N \overline{V}^2 \Rightarrow 3 \frac{R T}{N}=m \overline{V}^2 \text { or } \frac{1}{2} m \overline{V}^2=\frac{3}{2} K_B T\) [∵ \(\frac{R}{N}\) = KB]
Here KB is Boltzman constant. So mean kinetic energy of a molecule is \(\frac{3}{2}\) KB T, which depends upon the temperature. As temperature increases mean kinetic energy of the molecules also increases.
![]()
Question 2.
How specific heat capacity of mono atomic, diatomic and poly atomic gases can be explained on the basis of Law of equipartition of Energy ? [Mar. 13]
Answer:
Specific heat capacity:
1) Mono atomic gases : According to law of equipartition of energy, a molecule of mono atomic gas has only 3 (translational) degrees of freedom, i.e., f = 3.
The molar specific heat of the gas at constant volume is given by Cv = \(\frac{f}{2}\) R where f is degree of freedom.
∴ Cv = \(\frac{3}{2}\)R = 3 cal/mole k [∵ R = 2 cal/mole – k]
The molar specific heat at constant pressure is given by
Cp = (\(\frac{f}{2}\) + 1)R = (\(\frac{3}{2}\) + 1) R = \(\frac{5}{2}\)R = 5 cal/ m0le – k
2) Diatomic gases : A molecule of diatomic gas has 5 degrees of freedom, 3 translational and 2 rotational i.e., f = 5
Therefore Cv = \(\frac{f}{2}\) R = \(\frac{5}{2}\)R = 5 cal/mole – k, Cp = (\(\frac{f}{2}\) + 1) R = \(\frac{7}{2}\) R = 7 cal/mole – k
3) Polyatomic gases : Polyatomic molecule has 3 translational, 3 rotational degrees of freedom, i. e., f = 6
Therefore Cv = \(\frac{f}{2}\)R = 3R = 6 cal / mole – k, Cp = (\(\frac{f}{2}\) + 1) = 4R = 8 cal / mole – k.
Question 3.
Explain the concept of absolute zero of temperature on the basis of kinetic theory.
Answer:
Concept of absolute zero on the basis of kinetic theory :
Since the pressure of the gas is given by
P = \(\frac{1}{3} \mathrm{mn} \overline{\mathrm{V}}^2\), where m = mass of the gas, n = \(\frac{\mathrm{N}}{\mathrm{V}}\) = number of molecules per unit volume.
V = r.m.s velocity of gas, P = \(\frac{1}{3} \frac{\mathrm{mN}}{\overline{\mathrm{V}}} \overline{\mathrm{V}}^2\) ⇒ PV = \(\frac{1}{3} m N \overline{V}^2\)
Also for a gram molecule of the gas, PV = RT
Hence RT = \(\frac{1}{3} M \overline{V}^2\) [∵ M = mN = molecular weight]
\(\overline{\mathrm{V}}^2=\frac{3 R T}{M}\)
∴ \(\overline{v}=\sqrt{\frac{3 R T}{M}}\)
Putting T = 0 in the above equation \(\overline{\mathrm{V}}\) = 0. Hence pressure becomes zero. Then the gas converts into liquids. Thus, this temperature is called absolute zero.
![]()
Question 4.
Prove that the average kinetic energy of a molecule of an ideal gas is directly proportional to the absolute temperature of the gas.
Answer:
Since the pressure of the gas is given by
P = \(\frac{1}{3} \mathrm{mn} \overline{\mathrm{V}}^2\), where m = mass of the gas, n = \(\frac{\mathrm{N}}{\mathrm{V}}\) = number of molecules per unit volume
\(\) = r.m.s velocity of gas, P = \(\frac{1}{3} m \frac{N}{V} \overline{V}^2\) ⇒ PV = \(\frac{1}{3} \mathrm{mNV}^2\)
Also for a gram molecule of the gas, PV = RT
Hence RT = \(\frac{1}{3}\) mNV2
3\(\frac{\mathrm{R}}{\mathrm{V}}\)T = \(\mathrm{m} \overline{\mathrm{V}}^2\) or \(\frac{1}{2}\) mV2 = \(\frac{3}{2}\)KBT [∵ \(\frac{\mathrm{R}}{\mathrm{V}}\) = KB]
Where KB is the Boltzmann constant and T is the absolute temperature. ∴ E = \(\frac{3}{2}\)KBT
Hence the average kinetic energy of a molecule is proportional to the absolute temperature of the gas.
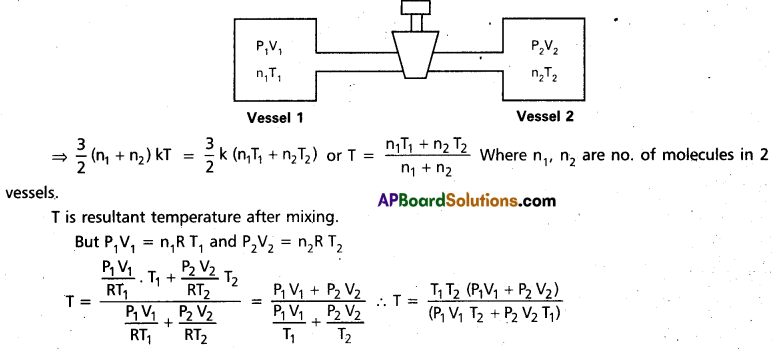
Question 5.
Two thermally insulated vessels 1 and 2 of volumes V1 and V2 are joined with a valve and filled with air at temperatures (T1, T2) and pressures (P1, P2) respectively. If the valve joining the two vessels is opened, what will be the temperature inside the vessels at equilibrium.
Answer:
During adiabatic process, there is no loss of energy, i.e. K.ET of molecules before mixing = K.ET of molecules after mixing.
Question 6.
What is the ratio of r.m.s speed of Oxygen and Hydrogen molecules at the same temperature ?
Answer:
The r.m.s speed of gas is \(\overline{\mathrm{V}}=\sqrt{\frac{3 R T}{M}} \Rightarrow \frac{\overline{\mathrm{V}}_0}{\mathrm{~V}_{\mathrm{H}}}=\sqrt{\frac{\mathrm{M}_{\mathrm{H}}}{\mathrm{M}_{\mathrm{O}}}}\), Given MH = 2 and M0 = 32
\(\frac{\overline{\mathrm{V}}_0}{\overline{\mathrm{V}}_{\mathrm{H}}}=\sqrt{\frac{2}{32}}=\frac{1}{4}\)
∴ V0 : VH = 1 : 4
![]()
Question 7.
Four molecules of a gas have speeds 1, 2, 3 and 4 km/s. Find the rms speed of the gas molecule.
Answer:
Given V1 = 1 km/s; V2= 2 km/s; V3 = 3 km/s; V4 = 4 km/s; = ?
Vrms = \(\sqrt{\frac{V_1^2+V_2^2+V_3^2+V_4^2}{n}}=\sqrt{\frac{1^2+2^2+3^2+4^2}{4}}\)
= \(\sqrt{\frac{1+4+9+16}{4}}=\sqrt{\frac{30}{4}}=\sqrt{7.5}\)
= 2735 kms-1
Question 8.
If a gas has ‘f’ degrees of freedom, find the ratio of CP and CV.
Answer:
If a gas has ‘f’ degrees of freedom, then
CV = \(\frac{f}{2}\)R and CP = CV + R = \(\frac{f}{2}\) R + R = (\(\frac{f}{2}\) + 1)R
Hence the ratio of the two specific heats of a gas is, r = \(\frac{C_p}{C_V}=\left[\frac{\frac{f}{2}+1}{\frac{f}{2} R}\right]=1+\frac{2}{f}\)
Question 9.
Calculate the molecular K.E of 1 gram of Helium (Molecular weight 4) at 127°C. Given R = 8.31 J mol-1 K-1.
Answer:
Given, t = 127°C, T = 273 + 127 = 400; R = 8.31 J mol-1 K-1
K.E. = \(\frac{3}{2}\)KBT = \(\frac{3}{2}\) × 1.38 × 10-23 × 400 = 8.28 × 10-21 J.
![]()
Question 10.
When pressure increases by 2%, what is the percentage decrease in the volume of a gas, assuming Boyle’s law is obeyed ?
Answer:
The gas obeys the Boyles law PV = constant, on differentiating, PdV + VdP = 0
PdV = – V dP ⇒ \(\frac{\mathrm{dV}}{\mathrm{V}}=\frac{-\mathrm{dP}}{\mathrm{P}}\) ⇒ \(\frac{\mathrm{dV}}{\mathrm{V}}\) × 100% = –\(\frac{-\mathrm{dP}}{\mathrm{P}}\) × 100%
% change in volume = – percentage change in pressure
∴ % change in volume = – 2%
Here negative sign indicates decrease in volume.
Long Answer Questions
Question 1.
Derive an expression for the Pressure of an ideal gas in a container from Kinetic Theory and hence give Kinetic Interpretation of Temperature.
Answer:
Let us consider cubical vessel of side T with perfectly elastic wall containing gas molecules. Let the three sides of the cube be taken as co-ordinate axis. Consider a molecule moving with velocity V, in any direction at any instant. The components of V1 along the three sides are Vx, Vy and Vz respectively. Then
\(\overline{V}^2=V_x^2+V_y^2+V_z^2\) ……………………. (1)
If ‘m is the mass of this molecule, it transfers a momentum mV when it strikes the face ABCD of the cube. Since the wall is perfectly elastic, this molecule is reflected back with a velocity – Vx and momentum – mVx. So the change in momentum = mVx – (- mVx)
= 2mVx
This molecule then travels towards the opposite face, collide with it, rebounds and travels again towards the face ABCD. The distance travelled between two successive collisions is 2l. Time taken between two successive collisions is \(\frac{2 l}{\mathrm{~V}_{\mathrm{x}}}\)
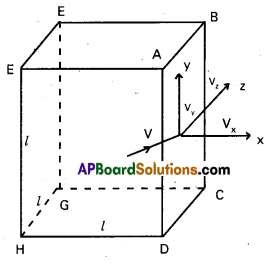
∴ Number of collisions per second = \(\frac{V_x}{2 l}\)
Change in momentum per second = (2mVx) × \(\left(\frac{\mathrm{V}_{\mathrm{x}}}{2 l}\right)=\frac{\mathrm{mV}_{\mathrm{x}}^2}{l}\)
Thus force exerted by this molecule = \(\frac{\mathrm{mV}_{\mathrm{x}}^2}{l}\) [∵ F = \(\frac{\mathrm{dP}}{\mathrm{dt}}\)]
Hence, force exerted by N such molecule in the X-direction.
f1 = \(\mathrm{N} \frac{\mathrm{mV}_{\mathrm{x}}^2}{l}=\frac{\mathrm{mNV}_{\mathrm{x}}^2}{l}\)
∴ Pressure exerted by the molecules in the x-direction is Px = \(\frac{f_1}{l^2}=\frac{m N \overline{V}_x^2}{l^3}\)
Similarly, pressure exerted by the molecules in the y and z-directions are
Py = \(\frac{\mathrm{m}}{l^3} \mathrm{~N} \overline{\mathrm{V}}_{\mathrm{y}}^2\) and Pz = \(\frac{\mathrm{m}}{l^3} \mathrm{~N} \overline{\mathrm{V}}_{\mathrm{z}}^2\)
Since the pressure exerted by a gas in all the directions is same, the average pressure
P = \(\frac{P_x+P_y+P_z}{3}=\frac{m N}{3 l^3}\left[V_x^2+v_y^2+V_z^2\right]=\frac{m N}{3 V} \overline{V}^2\) [ from (1) and V = l3]
Here V2 is the mean square velocity of the molecule, V is the volume of the vessel.
If M is the mass of the gas then M = mN
∴ P = \(\frac{1}{3} \frac{M^2}{V}=\frac{1}{3} m n \overline{V}^2\) [∵ n = \(\frac{N}{V}\)]
This pressure is actually the pressure exerted by an ideal gas.
![]()
b) Kinetic interpretation of temperature :
Since the pressure of the gas is given by
P = \(\frac{1}{3} m n \overline{V}^2\), where m = mass of the gas, n = \(\frac{N}{V}\) = Number of molecules per unit volume
\(\overline{V}\) = r.m.s velocity of gas
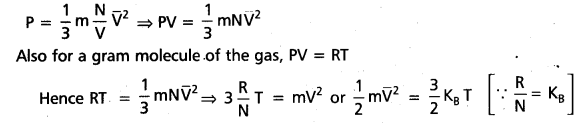
Here KB is Boltzmann constant. So mean kinetic energy of a molecule is \(\frac{3}{2}\) KBT, which depends upon the temperature. As temperature increases means kinetic energy of the molecules also increases.
Additional Problems
Question 1.
Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of an oxygen molecule to be 3 Å.
Solution:
Here, diameter,
d = 3A°, r = \(\frac{\mathrm{d}}{2}=\frac{3}{2}\) A° = \(\frac{3}{2}\) × 10-8 cm.
Molecular volume,
v = \(\frac{4}{3}\) πr3N, where N is Avagadros No.
= \(\frac{4}{3}\) × \(\frac{22}{7}\) (1.5 × 10-8)3 × (6.023 × 1023)
= 8.52 cc.
Actual volume occupied by 1 mole of oxygen at STP v = 22400 cc
= \(\frac{v}{v^{\prime}}=\frac{8.52}{22400}\) = 3.8 × 10-4 = 4 × 10-4.
Question 2.
Molar volume is the volume occupied by 1 mol of any (ideal) gas at standard temperature and pressure (STP : 1 atmospheric pressure, 0 °C.) Show that it is 22.4 litres.
Solution:
For one mole of an ideal gas, ρv = RT
∴ v = \(\frac{\mathrm{RT}}{\rho}\)
Put R = 8.31 J mole-1 k-1, T = 273k, ρ = 1 atm = 1.013 × 105 Nm-2
v = \(\frac{8.31 \times 273}{1.013 \times 10^5}\) = o.0224m3 = 0.0224 × 106
cc = 22400 cc = 22.4 lit.
![]()
Question 3.
Figure 14.8 shows plot of PV/T versus P for 1.00 × 10-3 kg of oxygen gas at two different temperatures.
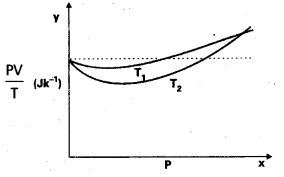
a) What does the dotted plot signify ?
b) Which is true: T1 > T2 or T1 < T2 ?
c) What is the value of PV/T where the curves meet on they y-axis ?
d) If we obtained similar plots for 1.00 × 10-3 kg of hydrogen, would we get the same value of PV/T at the point where the curves meet on the y-axis ? If not, what mass of hydrogen yields the same value of PV/T (for low pressurehigh temperature region of the plot) ? (Molecular mass of H2 = 2.02 u, of O2 = 32.0 u, R = 8.31 J mole-1 K-1.)
Solution:
a) The dotted plot shows that \(\frac{\mathrm{PV}}{\mathrm{T}}\) (= μR) is a constant quantity, independent of pressure p. This sign signifies the ideal gas behaviour.
b) The curve at temperature T1 is closer to dotted plot than the curve at temperature T2. As the behaviour of a real gas approaches the behaviour of a perfect gas when temperature is increased, therefore T1 > T2.
c) Where the two curves meet, the value of
\(\frac{\mathrm{PV}}{\mathrm{T}}\) on y-axis is equal to μR.
As mass of oxygen gas = 1.00 × 10-3 kg = 1g
\(\frac{\mathrm{PV}}{\mathrm{T}}\) = nR (\(\frac{1}{32}\)) × 8.31 Jk-1.
d) If we obtained similar plots for 1.00 × 10-3 kg of hydrogen, we will not get the same value of \(\frac{\mathrm{PV}}{\mathrm{T}}\) at the point, where the curve meets on the y-axis. This is because molecular mass of hydrogen is different from that of oxygen.
For same value of \(\frac{\mathrm{PV}}{\mathrm{T}}\) mass of hydrogen required is obtained from.
\(\frac{\mathrm{PV}}{\mathrm{T}}\) = nR = \(\frac{\mathrm{M}}{2.02}\) × 8.31 = 0.26
M = \(\frac{2.02 \times 0.26}{8.31}\) gm = 6.32 × 10-2 grams.
Question 4.
All oxygen cylinder of volume 30 litres has an initial gauge pressure of 15 atm and a temperature of 27 °C. After some oxygen is withdrawn from the cylinder, the gauge pressure drops to 11 atm and its temperature drops to 17 °C. Estimate the mass of oxygen taken out of the cylinder (R = 8.31 J mol-1 K-1, molecular mass of O2 = 32 u).
Solution:
Initially in the oxygen cylinder,
v1 = 30 lit = 30 × 10-3 m3
P1 = 15 atm = 15 × 1.01 × 105 Pa;
T1 = 27 + 273 = 300 k.
If the cylinder contains n1 mole of oxygen gas, then
P1v1 = nRT1
(or) n1 = \(\frac{\mathrm{P}_1 \mathrm{~V}_1}{\mathrm{RT}_1}=\frac{\left(15 \times 1.01 \times 10^5\right) \times\left(30 \times 10^{-3}\right)}{8.3 \times 300}\)
= 18.253 .
For oxygen, molecular weight, M = 32 g
Initial mass of cylinder,
M1 = n1 M = 18.253 × 32 = 584.1 g
Finally in the oxygen cylinder, let n2 moles of O2 be left, were,
v2 = 30 × 10-3 m3, P2 = 11 × 1.01 × 105 Pa, T2 = 17 + 273 = 29K
Now
n2 = \(\frac{\mathrm{P}_2 \mathrm{~V}_2}{\mathrm{RT}_2}=\frac{\left(11 \times 1.01 \times 10^5\right) \times\left(30 \times 10^{-3}\right)}{8.3 \times 290}\)
= 13.847
∴ Final mass of oxygen gas in the cylinder,
m2 = 13.847 × 32 = 453.1 g
∴ Mass of oxygen taken out = m1 – m2 = 631.0 g.
![]()
Question 5.
An air bubble of volume 1.0 cm3 rises from the bottom of a lake 40 m deep at a temperature of 12 °C. To what volume does it grown when it reaches the surface, which is at a temperature of 35 °C ?
Solution:
v1 = 1.0 cm3 = 1.0 × 10-6 m3,
T1 = 12 °C = 12 + 273 = 285 k
P1 = 1 atm + h1 ρg = 1.01 × 105 + 40 × 103 × 9.8
= 493000 Pa.
When the air bubble reaches at the surface of lake, then
v2 = 2, T2 = 35 °C = 35 + 273 = 308 K,
P2 = 10 atm = 1.01 × 105 pa.
Now \(\frac{P_1 v_1}{T_1}=\frac{P_2 v_2}{T_2}\) (or) v2 = \(\frac{P_1 v_1 T_2}{T_1 P_2}\)
∴ v2 = \(\frac{(493000) \times\left(1.0 \times 10^{-6}\right) \times 308}{285 \times 1.01 \times 10^5}\)
= 5.27 × 10-6m3.
Question 6.
Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity 25.0 m3 at a temperature of 27 °C and 1 atm pressure.
Solution:
Here, v = 25.0 m3, T = 27 + 273 = 300 k,
k = 1.38 × 10-23 Jk-1
Now Pv = nRT = n(NK) T = (nN) kT = N’kT
When nN = N’ = total no. of air molecules in the given gas.
N’ = \(\frac{\mathrm{Pv}}{\mathrm{kT}}=\frac{\left(1.01 \times 10^5\right) \times 25}{\left(1.38 \times 10^{-23}\right) \times 300}\) = 6.10 × 1026
Question 7.
Estimate the average thermal energy of helium atom at (i) room temperature (27 °C), (ii) the temperature on the surface of the Sun (6000 K), (iii) the temperature of 10 million kelvin (the typical core temperature in the case of a star).
Solution:
i) Here, T = 27 °C = 27 + 273 = 300 k
Average thermal energy
= \(\frac{3}{2}\) kT = \(\frac{3}{2}\) × 1.38 × 10-23 × 300
= 6.2 × 10-21 J
ii) At T = 6000 k. Average thermal energy = \(\frac{3}{2}\)kT = \(\frac{3}{2}\) × 1.38 × 10-23 × 6000
= 1.24 × 10-19 J.
iii) At T = 10 million K = 107 K.
Average thermal energy
= \(\frac{3}{2}\)kT = \(\frac{3}{2}\) × 1.38 × 10-23 × 107
= 2.1 × 10-16 J.
![]()
Question 8.
Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (poly-atomic). Do the vessels contain equal number of respective molecules ? Is the root mean square speed of molecules the same in the three cases ? If not, in which case is urms the largest ?
Solution:
All the three vessels (at the same temperature and pressure) have same volume. So in accordance with the avagadro’s law, the three vessels will contain equal number of respective molecules, being equal to
Avagadro’s number N = 6.023 × 1023
As vrms = \(\sqrt{\frac{3 k T}{m}}\)
i.e., vrms ∝ \(\frac{1}{\sqrt{m}}\) at a given temp, therefore, rms speed of molecules will not be same in the three cases.
As neon has the smallest mass, therefore, rms speed will be largest in case of neon.
Question 9.
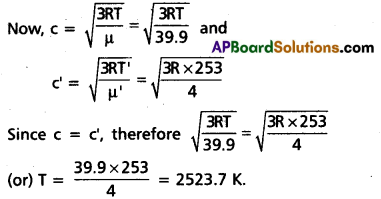
At what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the rms speed of a helium gas atom at – 20 °C ? (atomic mass of Ar = 39.9 u, of He = 4.0 u).
Solution:
Let c and c’ be the rms velocity of argon and a helium gas atoms at temperature TK and TK’ respectively.
Here μ = 39.9, μ = 4.0,
T = 2, T’ = -20 + 273 = 253 K.
Question 10.
Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at 2.0 atm and temperature 17 °C. Take the radius of a nitrogen molecule to be roughly 1.0 Å. Compare the collision time with the time the molecule moves freely between two successive collisions (Molecular mass of N2 = 28.0 u).
Solution:
Here, λ = 2, f = 2
P = 2 atm = 2 × 1.013 × 105 Nm-2
T = 17 °C = (17 + 273) K = 290 k
σ = 2 × 1 = 2A° = 2 × 10-10 m
K = 1.38 × 10-23 J molecule-1 k-1,
μ = 28 × 10-3 kg
λ = \(\frac{\mathrm{KT}}{\sqrt{2} \pi \sigma^2 \rho}\)
= \(\frac{1.38 \times 10^{-23} \times 290}{1.414 \times 3.14\left(2 \times 10^{-10}\right)^2 \times 2.026 \times 10^5}\)
λ = \(\frac{1.38 \times 29 \times 10^{-7}}{1.44 \times 3.14 \times 2.06}\) = 1.11 × 10-7 m.
vrms = \(\sqrt{\frac{3 R T}{M}}=\sqrt{\frac{3 \times 8.31 \times 290}{28 \times 10^{-3}}}\) = 508.24 m/s.
Collision frequency = no. of collisions per second = \(\frac{v_{r m s}}{\lambda}=\frac{508.24}{1.11 \times 10^{-7}}\) = 4.58 × 109
![]()
Question 11.
A metre long narrow bore held horizontally (and closed at one end) contains a 76 cm long mercury thread, which traps a 15 cm column of air. What happens if the tube is held vertically with the open end at the bottom ?
Solution:
When the tube is held horizontally, the mercury of length 76 cm traps length of air = 15 cm. A length of 9 cm of the tube will be left at the open end. Fig. (a). The pressure Of air enclosed in tube will be atmospheric pressure. Let area of cross section of the tube be 1 sq.cm.
∴ P1 = 76 cm and v1 = 15 cm3.
When the tube is held vertically, 15 cm air gets another 9 cm of air (filled in the right hand side position) and let h cm of the mercury flows out to balance the atmospheric pressure. Fig. (b). Then the heights of air column and mercury column are (24 + h) cm and (76 – h) cm respectively.
The pressure of air = 76 – (76 – h) = h cm of mercury
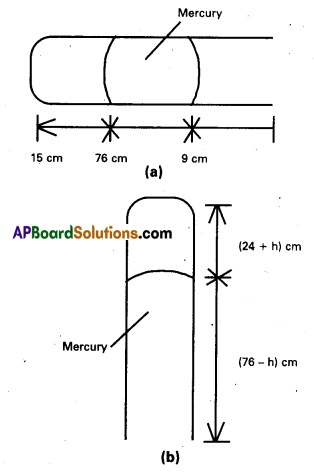
∴ v2 = (24 + h) cm3 and P2 = hcm.
If we assume that temperature remains constant, then
P1v1 = P2v1 or 76 × 15 = h × (24 + h) or h2 + 24h – 1140 = 0
(or) h = \(\frac{-24 \pm \sqrt{(24)^2+4 \times 1140}}{2}\) = 23.8 cm
(or) -47.8 cm.
Since h cannot be negative, therefore h = 23.8 cm.
In vertical position it flows out (23.8) cm.
Question 12.
From a certain apparatus, the diffusion rate of hydrogen has an average value of 28.7 cm3s-1. The diffusion of another gas under the same conditions is measured to have an average rate of 7.2 cm3s-1. Identify the gas.
[Hint: Use Graham’s law of diffusion : R1/R2 = (M2/M1) where R1, R2 are diffusion rates of gases 1 and 2 and M1 and M2 their respective molecular masses. The law is a simple consequence of kinetic theory.]
Solution:
According to Graham’s law of diffusion
\(\frac{r_1}{r_2}=\sqrt{\frac{M_2}{M_1}}\)
Where
r1 = diffusion rate of hydrogen = 28.7 cm3s-1
r2 = diffusion rate of unknown gas = 7.2 cm3s-1
M1 = molecule wt. of hydrogen = 2u M2 = ?
M2 = ?
∴ \(\frac{28.7}{7.2}=\sqrt{\frac{\mu_2}{\mu_1}} \text { or } M_2=\left(\frac{28.7}{7.2}\right)^2 \times 2\) = 31.78
≈ 32 µ
![]()
Question 13.
A gas in equilibrium has uniform density and pressure throughout its volume. This is strictly true only if there are no external influences. A gas column under gravity, for example, does not have uniform density (and pressure). As you might expect, its density decreases with height. The precise dependence is given by the so- called law of atmospheres.
n2 = n1 exp [-mg(h2 – h1)/KBT] Where n2, n1 refer to number density at heights h2 and h1 respectively. Use this relation to derive the equation for sedimentation equilibrium of a suspension in a liquid column :
n2 = n1 exp [-mg NA (ρ – P) (h2 – h1)/(ρRT]
Where ρ is the density of the suspended particle and ρ that of surrounding medium. [NA is Avogadro’s number and R the universal gas constant.]
[Hint: Use Archimedes principle to f ind the apparent weight of the suspended particle.]
Solution:
According to the law of atmospheres n2 = n1 exp. [-\(\frac{m g}{K_B T}\) (h2 – h1)] ………… (1)
Where n2 n1 refer to number density of particles at heights h2 and h1 respectively. If we consider the sedimentation equilibrium of suspended particles in a liquid, then in place of mg, we will have to take effective weight of suspended particles.
Let
v = average vol. of suspended particle
ρ = density of suspended particle
ρ’ = density of liquid
m = mass of one suspended particle
m’ = mass of equal vol. of liquid displaced
According to Archimedis principle, effective weight of one suspended particle.
= actual weight – weight of liquid displaced
= mg – m’ g
= mg – v P’g = mg – (m/P) P’g = mg \(\left(\frac{1-\rho^{\prime}}{\rho}\right)\)
Also boltzman constant, KB = \(\frac{R}{N A}\) ………….. (i)
Where R is gas constant and NA is Avagadros number.
Putting mg \(\left(\frac{1-\rho^{\prime}}{\rho}\right)\) in place of mg and value of KB in (i).
We get
n2 = n1 exp \(\left[-\frac{\text { mgNA }}{R T} \cdot\left(1-\frac{\rho^{\prime}}{\rho}\right)\left(h_2-h_1\right)\right]\)
Which is the required relation.
![]()
Question 14.
Given below are densities of some solids and liquids. Give rough estimates of the size of their atoms :
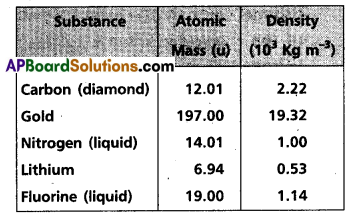
[Hint: Assume the atoms to be tightly packed1 in a solid or liquid phase, and use the known value of Avogadro’s number. You should, however, not take the actual numbers you obtain for various atomic sizes too literally. Because of the crudeness of the tight packing approximation, the results only indicate that atomic sizes are in the range of few Å].
Solution:
If r is the radius of the atom, then volume of each atom = \(\frac{4}{3}\) πr3
Volume of all atoms in one mole of substance
= \(\frac{4}{3}\) πr3 × N = μ/P
r = \(\left[\frac{3 \mu}{4 \pi \mathrm{PN}}\right]^{\frac{1}{3}}\)
For carbon p = 12.01 × 10-3 kg,
P = 2.22 × 103 kg m-3
r = \(\frac{3 \times 12.01 \times 10^{-3}}{4 \times \frac{22}{7} \times\left(2.2210^3\right) \times\left(6.02310^{23}\right)}\)
r = 1.29 × 10-10 m = 1.29A°
Similarly for gold
r = 1.59A°
For liquid nitrogen r = 1.77A°
For lithium r = 1.73A°
For liquid fluorine r = 1.88A°
Textual Examples
Question 1.
The density of water is 1000 kg m-3. The density of water vapour at 100° C and 1 atm pressure is 0.6 kg m-3. The volume of a molecule multiplied by the total number gives. What is called, molecular volume. Estimate the ratio (or fraction) of the molecular volume to the total volume occupied by the water vapour under the above conditions of temperature and pressure.
Answer:
For a given mass of water molecules, the density is less if volume is large. So the volume of the vapour is 1000/0.6 = /(6 × 10-4) times, large. If densities of bulk water and water molecules are same, then the fraction of molecular volume to the total volume in liquid state is 1. As volume in vapour state has increased, the fractional volume is less by the same amount, i.e. 6 × 10-4.
![]()
Question 2.
Estimate the volume of a water molecule using the data in Example 1.
Answer:
In the liquid (or solid) phase, the molecules of water are quite closely packed. The density of water molecule may therefore, be regarded as roughly equal to the density of bulk water = 1000 kgm-3. We know that 1 mole of water has a mass approximately equal to (2 + 16)g = 18 g = 0.018 kg.
Since 1 mole contains about 6 × 1023 molecules (Avogadro’s number).
The mass of a molecule of water is (0.018) / (6 × 1023) kg = 3 × 10-26 kg.
Volume of a water molecule = (3 × 10-26 kg) (1000 kg m-3)
= 3 × 10-29 m3
= (4/3)π (Radius)3
∴ Radius » 2 × 10-10 m = 2Å
Question 3.
What is the average distance between atoms (interatomic distance) in water ? Use the data given in Examples 1 and 2.
Answer:
A given mass of water in vapour state has 1.67 × 103 times the volume of the same mass of water inliquid state (e.g. 1). When volume increases by 103 times the radius increases by V1/3 or 10 times,
i.e., = 10 × 12 = 2Å.
So the average distanceis 2 × 10 40 Å.
Question 4.
A vessel contains two non-reactive gases : neon (monatomic) and oxygen (diatomic). The ratio of their partial pressures is 3 : 2. Estimate the ratio of (i) number of molecules and (ii) mass density of neon and oxygen in the vessel. Atomic mass of Ne = 20.2 u, molecular mass of O2 = 32.0 u.
Answer:
Each gas (assumed ideal) obeys the gas law. Since V and T are common to the two gases, we have P1V = μ1 RT and P2V = μ2 RT. i.e., (P1 / P2) = (μ1 / p2). Here 1 and 2 refer to neon and oxygen respectively.
Since (P1 / P2) = (3/2) (given), (μ1 / μ2) = 3/2.
i) By definition μ1 = (N1 /NA) and μ2 = (N2/NA) where N1 and N2 are the number of molecules of 1 and 2, and NA is the Avogadro’s number. Therefore,
(N1/N2) = (μ1/μ2) = 3/2.
ii) We can also write μ1 = (m1/ M1) and μ2 = (m2 / M2) where m1 and m2 are their molecular masses. (Both m1 and M1; as well as m2 and M2 should be expressed in the same units). If ρ1 and ρ2 are the mass densities of 1 and 2 respectively, we helve
\(\frac{\rho_1}{\rho_2}=\frac{m_1 / V}{m_2 / V}=\frac{m_1}{m_2}=\frac{\mu_1}{\mu_2} \times\left[\frac{M_1}{M_2}\right]\)
= \(\frac{3}{2} \times \frac{20.2}{30.2}\) = 0.947
![]()
Question 5.
A flask contains argon and chlorine in the ratio of 2 : 1 by mass. The temperature of the mixtures is 27° C. Obtain the ratio of (i) average kinetic energy per molecule and (ii) root mean square speed vrms of the molecules of the two gases. Atomtic mass of argon = 39.9 u. Molecular mass of chlorine = 70.9 u.
Answer:
The important point to remember is that the average kinetic energy (per molecule) of any (ideal) gas (be it monatomic like argon, diatomic like chlorine or polyatomic) is always equal to (3/2) kBT. It depends only on temperature and is independent of the nature of the gas.
i) Since argon and chlorine both have the same temperature in the flask, the ratio of average kinetic energy (per molecule) of the two gases is 1 : 1.
ii) Now 1/2 mvrms2 = average kinetic energy . per molecule = (3/2) KBT where m is the mass of a molecule of the gas. Therefore,
\(\frac{\left(\mathrm{V}_{\mathrm{rms}}^2\right)_{A \mathrm{C}}}{\left(\mathrm{V}_{\mathrm{ms}}^2\right)_{\mathrm{cl}}}=\frac{(\mathrm{m})_{\mathrm{C}}}{(\mathrm{m})_{\mathrm{Ar}}}=\frac{(\mathrm{M})_{\mathrm{Cl}}}{(\mathrm{M})_{\mathrm{Ar}}}=\frac{70.9}{39.9}\) = 1.77
where M denotes the molecular mass of the gas.
\(\frac{\left(\mathrm{V}_{\text {rms }}\right)_{\mathrm{Ar}}}{\left(\mathrm{V}_{\mathrm{rms}}\right)_{\mathrm{cl}}}\) = 1.33
Question 6.
a) When a molecule (or an elastic ball) hits a (massive) wall, it rebounds with the same speed. When a ball hits a massive bat held firmly, the same thing happens. However, when the bat is moving towards the ball, the ball rebounds with a different speed. Does the ball move faster or slower ? (ch. 6 will refresh your memory on elastic collisions).
b) When gas in a cylinder is compressed by pushing in a piston, its temperature rises. Guess at an explanation of this in terms of kinetic theory using (a) above.
c) What happens when a compressed gas pushes a piston out and expands. What would you observe ?
d) Sachin Tendulkar uses a heavy cricket bat while playing. Does it help him in anyway ?
Answer:
a) Let the speed of the ball be u relative to the wicket behind the bat. If the bat is moving towards the ball with a speed V relative to the wicket, then the relative speed of the ball to bat is V + u towards the bat. When the ball rebounds (after hitting the massive bat) its speed, relative to bat, is V + u moving away from the bat. So relative to the wicket the speed of the rebounding ball is V + (V + u) = 2V + u, moving away from the wicket. So the ball speeds up after the collision with the bat. The rebound speed will be less than u if the bat is not massive. For a molecule this would imply an increase in temperature.
You should be able to answer (b) (c) and (d) based on the answer to (a).
![]()
Question 7.
A cylinder of fixed capacity 44.8 litres contains helium gas at standard temperature and pressure. What is the amount of heat needed to raise the temperature of the gas in the cylinder by 15.0° C ? (R = 8.31 J mol-1 K-1).
Answer:
Using the gas law PV = μRT, you can easily show that 1 mol of any (ideal) gas at standard temperature (273 K) and pressure (1 atm = 1.01 × 105 Pa) occupies a volume of 22.4 litres. This universal volume is called molar volume. Thus the cylinder in this example contains 2 mol of helium. Further, since helium is monatomic, its predicted (and observed) molar specific heat at constant volume, Cv = (3/2) R, and molar specific heat at constant pressure, Cp = (3/2) R + R =(5/2) R. Since the volume of the cylinder is fixed, the heat required is determined by Cv.
Therefore,
Heat required = no. of moles × molar specific heat × rise in temperature
= 2 × 1.5 R × 15.0 = 45
R = 45 × 8.31 = 374 J.
Question 8.
Estimate the mean free path for water molecule in water vapour at 373 K. Use information from Exercises 1 and above. l = 2.9 × 10-7 m = 1500d.
Ans. The d for water vapour is same as that of air. The number density is inversely proportional to absolute temperature.
So n = 2.7 × 1025 × \(\frac{273}{373}\) = 2 × 1025 m-3
Hence, mean free path l = 4 × 10-7 m.