Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 11th Lesson Mechanical Properties of Fluids Textbook Questions and Answers.
AP Inter 1st Year Physics Study Material 11th Lesson Mechanical Properties of Fluids
Very Short Answer Questions
Question 1.
Define average pressure. Mention it’s unit and dimensional formula. Is it a scalar or a vector ? [A.P. Mar. 17]
Answer:
Average pressure (Pav) : Average power is defined as the normal force acting per unit area.
Pav = \(\frac{F}{A}\)
units → N/m2 (or) pascal
Dimensional formula → [ML-1 T-2]
Pressure is a scalar quantity.
Question 2.
Define Viscosity. What are it’s units and dimensions ?
Answer:
Viscosity : The property of a liquid which opposes the relative motion between its layers is called viscosity. .
G.G.S unit poise
S.I unit → Nm-2s
Dimensional formula = [M1L-1T-1]
![]()
Question 3.
What is the principle behind the carburetor of an automobile ? [AP – Mar. 15; TS – Mar. ’18, ’17]
Answer:
The carburetor of automobile has a venturi channel (nozzle) through which air flows with a large speed. The pressure is then lowered at the narrow neck and the petrol is sucked up in the chamber to provide the correct mixture of air to fuel necessary for combustion. ”
Question 4.
What is magnus effect ? [T.S. Mar. 16; A.P. Mar. 15]
Answer:
The difference in the velocities of air results in the pressure difference between the lower and upper faces and there is a net upward force on the ball. This dynamic lift due to spinning is called magnus effect.
Question 5.
Why are drops and bubbles spherical ? [A.P. Mar. 18, 17, 16, 14]
Answer:
The surface tension of a liquid tends to have minimum surface area. For a given volume, the surface area is minimum for a sphere. Hence rain drops are spherical shape.
Question 6.
Give the expression for the excess pressure in a liquid drop. [T.S. Mar. 17]
Answer:
Excess pressure in a liquid drop, pi – p0 = \(\frac{2 s}{r}\)
where s = Surface tension; r = Radius of the liquid drop.
Question 7.
Give the expression for the excess pressure in an air bubble inside the liquid.
Answer:
Excess pressure in an air bubble inside the liquid, pi – p0 = \(\frac{2 s}{r}\)
where s = Surface tension
r = Radius of the air bubble.
Air bubble forms inside the liquid, hence it has one liquid surface.
![]()
Question 8.
Give the expression for the excess pressure soap bubble in air. [T.S. Mar. 16]
Answer:
Soap bubble have two interfaces, hence excess pressure inside a soap bubble is pi – p0 = \(\frac{4 s}{r}\)
where s = Surface tension
r = Radius of the soap bubble.
Question 9.
What are water proofing agents and water wetting agents ? What do they do ?
Answer:
Water proofing agents are added, to create a large angle of contact between water and fibres.
Soaps, detergents and dying substances are wetting agents. When they are added, the angle of contact becomes small. So that they may penetrate well and become effective.
Question 10.
What is angle of contact ? [A.P. Mar. 16]
Answer:
The angle between tangent to the liquid surface at the point of contact and solid surface inside the liquid is termed as angle of contact (0).
Question 11.
Mention any two examples that obey Bernoullis theorem and justify them. [A.P. Mar. 18]
Answer:
- In heavy winds house roof’s are blown off. When the velocity of the wind is greater on the roof top than inside the house, then the pressure on the roof top becomes less than that inside the house. This pressure difference causes the dynamic lift.
- When a fan is rotating, papers are blown off from .the table top. The velocity of wind on the paper increases due to fan and hence pressure decreases. Due to this pressure difference papers are blown off.
![]()
Question 12.
When water flows through a pipe, which of the layers moves fastest and slowest ?
Answer:
Water flows through a pipe, the layers near the axis of the tube are fastest and at the walls of the tube are slowest
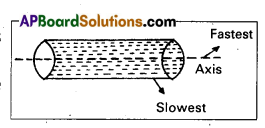
Question 13.
“Terminal velocity is more if surface area of the body is more”. Give reasons in support of your answer.
Answer:
Surface area (A) = 4πr2 and terminal velocity (υt) αr2
As surface area increases, r2 is also increases. Then terminal velocity is also increases.
∴ Terminal velocity is more, if surface area of the body is more.
Short Answer Questions
Question 1.
What is atmospheric pressure and how is it determined using Barometer ?
Answer:
Atmospheric pressure : Atmospheric pressure at any point is equal to the weight of a column of air of unit cross sectional area extending from that point to the top of the earth’s atmosphere.
1 atm = 1.013 × 105 pa
Determination of atmospheric pressure using barometer: A long glass tube closed at one end and filled with mercury is inverted into a trough of mercury. This device is known as mercury barometer.
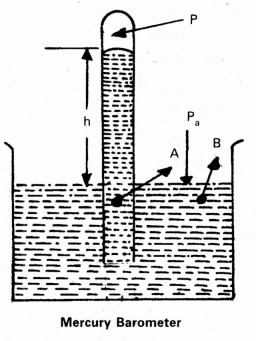
The space above the mercury column in the tube contains only mercury vapour whose pressure Pis so small, that it may be neglected. The pressure inside the column at point A must equal the pressure at B.
∴ Pressure at B = Atmospheric pressure = Pa
Pa = ρgh = Pressure at A …………………… (1)
Where ρ is density of mercury and h is the height of the mercury column in the tube. In the experiment it is found that the mercury column in the barometer has a height of about 76cm at the sea level equivalent to one atmosphere.
![]()
Question 2.
What is guage pressure and how is a manometer used for measuring pressure differences ?
Answer:
Guage pressure : The guage pressure is the difference of the actual pressure and the atmospheric pressure. Pg = P – Pa
measurement of pressure differences :
- The manometer consists of a U-shaped tube, which is filled with a low density liquid (oil) for measuring small pressure difference and high density liquid
(mercury) for measuring large pressure difference. - One end of the tube is connected to the vessel D whose pressure of air measure and the other end of the tube is open.
- If pressure of air in vessel D is more than the earth’s atmosphere, the level of liquid in arm I will go down up to point A and level of liquid in arm II rises up to C.
- Then the pressure of air in vessel is equal to pressure at point A.
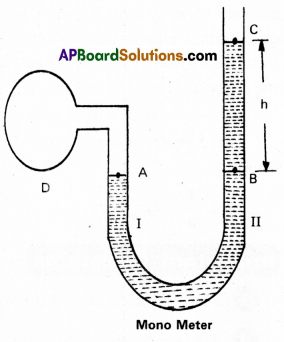
- Note the difference of liquid levels in the two arms of U-tube.(Say h). p be density of the liquid. Pa is the atmospheric pressure.
- Pressure at point A (PA) = Pressure at point B = Pressure at point C + Pressure due to column of liquid.
PA = Pc + hρg (or) PA – Pc = hρg
Here Pc = Pa, PA = P, ∴ P – Pa = hρg
P – Pa = Pg = guage pressure = hρg
Question 3.
State Pascal’s law and verify it with the help of an experiment.
Answer:
Pascal’s law : It states that if gravity effect is neglected, the pressure at every point of liquid in equilibrium of rest is same.
Proof :
- Imagine a circular cylinder of uniform cross-sectional area A, such that points C and D lie on flat faces of the cylinder.
- The liquid inside the cylinder is in equilibrium under the action of forces exerted by the liquid outside the cylinder.
- These forces are acting every where perpendicular to the surface of the cylinder.
- Thus the forces on the flat faces of the cylinder at C and D will be perpendicular to the forces on the curved surface of the cylinder.
- Since liquid is in equilibrium, the sum of the forces acting on the curved surface of the cylinder must be zero.
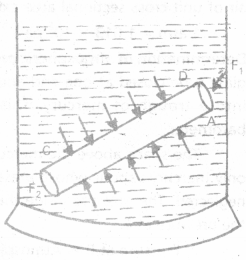
- If P1 and P2 are the pressures at points C and D respectively. F1 and F2 are the forces acting on the flat surfaces of the cylinder due to liquid, then
F1 = P1 A and F2 = P2A Since liquid is in equilibrium, therefore
F1 = F2
P1 A = P2A
(or) P1 = P2
It means the pressures at C and D are the same. This proves the pascal’s law.
![]()
Question 4.
Explain hydraulic lift and hydraulic brakes.
Answer:
Hydraulic lift and hydraulic brakes are based on the Pascal’s law.
Hydraulic lift : Here C and D are two cylinders of different areas of cross section. They are connected to each other with a pipe E. Each cylinder is provided with airtight frictionless piston. Let a, A be the area’s of cross-sections of the piston at C and D (a < < A)
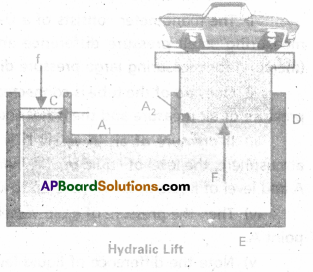
The cylinders are filled with an incompressible liquid.
Let f be the applied force at C. Pressure exerted on the liquid
P = \(\frac{f}{a}\) ……………. (1)
According to pascal’s law, this pressure is transmitted to piston of cylinder D. Upward force at D will be
F = PA = \(\frac{f}{a}\) A = f \(\frac{A}{a}\) …………… (2)
As A > > a
∴ F > > f .
∴ Heavy load placed on the larger piston is easily lifted.
Hydraulic Brakes :
When the brake pedal is pressed, the piston (P) of the master cylinder is pushed inwards. There will be increased pressure on liquid at P, which is transmitted equally to P1 and P2 of wheel cylinder in accordance with pascal’s law. Due to which P1 and P2 move outwards. Breakshoes to move away from each other which in turn press against the inner rim of the wheel. The brake becomes operative.
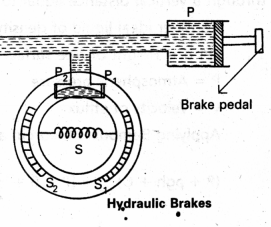
Question 5.
What is hydrostatic paradox ?
Answer:
Consider three vessels A, B and C of different shapes. They are connected at the bottom by a horizontal pipe. On filling with the level in the three vessels is the same, though they hold different amounts of water. This is so because water at the bottom has the same pressure below each section of the vessel. It means the liquid pressure at a point is independent of the quantity of liquid but depends upon the depth of point below the liquid surface. This is known as hydrostatic paradox.
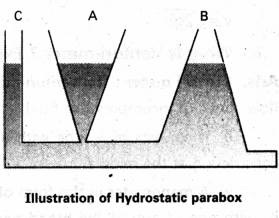
![]()
Question 6.
Explain how pressure varies with depth.
Answer:
Consider a fluid at rest in a container. In figure point 1 is at a height h above a point 2. The pressure at points 1 and 2 are P1 and P2. As the fluid is at rest, the horizontal forces should be zero. The resultant vertical forces should balance the weight of the element. Pressure at top (P1A) acting downward, pressure at bottom (P2A) acting upward.
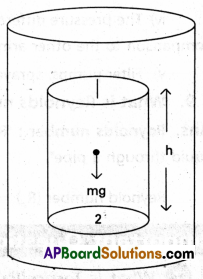
(P2 – P1) A = mg ………………… (1)
Mass of the fluid (m) = ρv = ρhA
(P2 – P1) = ρgh ………………. (2)
Pressure difference depends on the vertical distance h.
If the point 1 under discussion is shifted to the top of the fluid (water), which is open to the atmosphere, P1 may be replaced by atmospheric pressure (Pa) and P2 by P. Then eq (2) gives
P – Pa = ρgh
P = Pa + ρgh ……………… (3)
Thus the pressure P, at depth below the surface of a liquid open to the atmosphere is greater than atmospheric pressure by an amount ρgh.
Question 7.
What is Torricelli’s law ? Explain how the speed of efflux is determined with an experiment.
Answer:
Torricelli’s theorem : The velocity of efflux i.e., the velocity with which the liquid flows out of an orifice (i.e., a narrow hole) is equal to that which is freely falling body would acquire in falling through a vertical distance equal to the depth of orifice below the free surface of liquid.
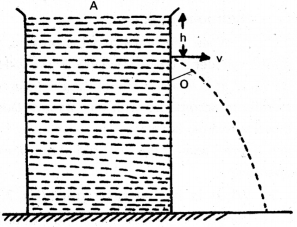
Consider ideal liquid of density p contained in a tank provided with a narrow hole.
Let h = Height of free surface of liquid above O.
P = Atmospheric pressure
v = Velocity of efflux
Applying Bernoulli’s theorem at A and O
(P + ρgh + O)atA = [P + 0 + \(\frac{1}{2}\)ρv2]atO
P + ρgh = P + \(\frac{1}{2}\) ρv2 = ρgh = \(\frac{1}{2}\)ρv2
v = \(\sqrt{2 g h}\)
![]()
Question 8.
What is Venturi-meter? Explain how it is used.
Answer:
Venturi meter: The Venturi-meter is a device to measure the flow speed of incompressible fluid.
- It consists of a tube with a broad diameter and a small constriction at the middle.
- A manometer in the form of a U-tube is also attached to it, with one of arm at the broad neck point of the tube and the other at constriction as shown in figure.
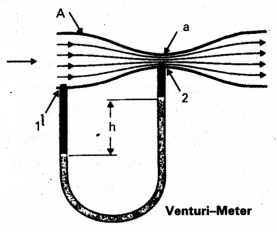
- The manometer contains a liquid of density ρm.
- The pressure difference causes the fluid in the U-tube connected at the narrow neck to rise in comparison to the other arm.
- Filter pumps, sprayers used for perfumes, carburetor of automobile has used on this principle.
Question 9.
What is Reynolds number ? What is it’s significance ?
Answer:
Reynolds number : “Reynold number is a pure number which determines the nature of flow of liquid through a pipe”.
Reynold number (Re) = \(\frac{\rho \mathrm{vd}}{\eta}\)
Where ρ is density of the fluid
v is speed of the fluid
d is diameter of the pipe
- If the flow is stream line (or) laminor Re < 1000
- If the flow is turbulent, Re > 2000
- If the flow becomes unsteady, 1000 < Re < 2000
Physical significance of Reynolds number : Reynold’s number describes the ratio of the inertial force per unit area to the viscous force per unit area for a flowing fluid.

![]()
Question 10.
Explain dynamic lift with examples.
Answer:
Dynamic lift: Dynamic lift is the force that act on a body, by virtue of its motion through a fluid.
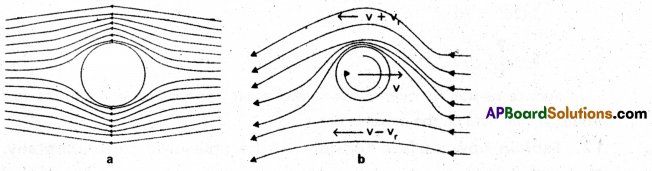
e.g.1 : Fig (a) shows, ball moving without spin. Stream lines are equally distributed above and below the ball. The velocity above and below the ball is same resulting zero pressure difference. There no upward (or) downward force on the ball.
Fig (b) shows, ball moving with spin stream lines are more crowded above the ball than below. The velocity of air above the ball is large (v + vr) and below it is smaller (v – vr). As a result, there is a pressure difference between lower and upper faces. Pressure is less at top of the ball and pressure is morebelow the ball. There is a net upward force on the ball.
e.g. 2 : Dynamic lift also acts on the an aeroplane wing.
Question 11.
Explain Surface Tension and Surface energy. [Mar. 13]
Answer:
Surface tension (S): The force acting per unit length of an imaginary line drawn on the surface of a liquid, normal to it and parallel to the surface is called surface tension.
T = \(\frac{\mathrm{F}}{l}\)
S.l unit → N/m
D.F → [MT-2]
Surface energy (E): The additional potential energy due to molecular forces per unit surface area is called surface tension.
Surface energy = \(\)
S.l Unit → J/m2
D.F → (MT-2 )
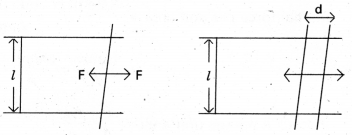
Consider a horizontal liquid film ending in bar free to slide over parallel guides. We move the bar by a small distance d. The area of the surface increases, the system now has more energy, this means – that some work has to be done against an internal force F.
Work done (W) = F.d
If the surface energy of the film is S per unit area, the extra area is 2dl. A film has two sides and the liquid in between them.
So there are two surfaces and the extra energy is
S (2dl) = Fd
S = \(\frac{\mathrm{F}}{2 l}\)
Surface tension is equal to the surface energy and is also equal to the force per unit length exerted by the fluid on the movable bar.
![]()
Question 12.
Explain how surface tension can be measured experimentally.
Answer:
A flat vertical glass plate, below which a vessel of some liquid is kept, forms one arm of the balance. The plate is balanced by weights on the otherside, with its horizontal edge just over water. The vessel is raised slightly till the liquid just touches the glass plate and pulls it down a little because of surface tension. Weights are added till the plate just clears water. Suppose the additional weight requires is W.
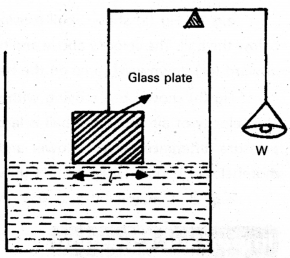
Surface tension of liquid air interface is
Sla = \(\frac{\mathrm{W}}{2 l}=\frac{\mathrm{mg}}{2 l}\)
Where l is length of the plate edge, m is extra mass.
Long Answer Questions
Question 1.
State Bernoulli’s principle. From conservation of energy in a fluid flow through a tube, arrive at Bernoulli’s equation. Give an application of Bernoulli’s theorem.
Answer:
Bernoulli’s principle : Bernoulli principle states that in a stream line flow, the sum of the pressure, the K.E per unit volume and the P.E per unit volume remains a constant.
P + \(\frac{1}{2}\) ρv2 + ρgh = constant
- Consider a non-viscous, incompressible fluid is flowing through the pipe in a steady flow.
- Consider the flow at two regions BC and DE. Initially the fluid lying between B and D.
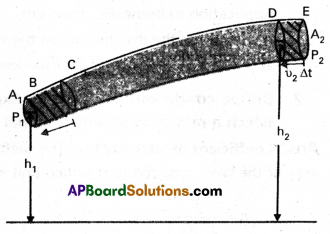
- During short time interval At, this fluid would have moved. Suppose V1 is the speed at B and V2 is the speed at D.
- In time ∆t, distance moved from B to C is V1 ∆t in the same interval (∆t) distance moved from D to E is V2∆t.
- Let P1 and P2 be pressure act at area’s of cross¬sections A1 and A2 of the two regions.
- The work done on the fluid at left end (BC)
= Force × displacement
= Pressure × Area × displacement
= P1A1 × V1∆t (∆V = A1V1∆t) = P1∆V ………………. (1) - Similarly work done by the fluid at right end (DE)
= P2A2 × V2∆t = P2∆V …………………. (2) - Work done on the fluid is taken as positive and workdone by the fluid is taken as negative.
∴ Total work done (W) = (P1 – P1) ∆V ………………. (3)
Part of this work goes into changing the K.E of the fluid and part goes into changing gravitational P.E. - Mass of the fluid(∆m) passing through the pipe in time (∆t) is ∆m = ρA1V1∆t
where ρ is the density of the fluid.
∆m = ρ∆V ………………….. (4) - Gravitational P.E = ρg∆V (h2 – h1) ………………… (5)
Change in K.E (∆K) = \(\frac{1}{2}\) ρ∆V (V22 – V12) …………….. (6) - According to law of conservation of energy
(P1 – P2) ∆V = \(\frac{1}{2}\) ρ ∆V (V22 – V12) + ρg∆V (h2 – h1)
P1 – P2 = \(\frac{1}{2}\) ρ (V22 – V12) + ρg (h2 – h1)
P1 + \(\frac{1}{2}\) ρ V12 + ρgh1 = P1 + \(\frac{1}{2}\) ρ V22 + ρgh2
P + \(\frac{1}{2}\) ρ v2 + ρgh = constant ………………. (7)
∴ Sum of the pressure, K.E per unit volume and P.E per unit volume remains constant. Application of Bernoulli’s theorem :
- It explains the dynamic lift on the wings of aeroplanes.
- It explains the dynamic lift experienced by a spinning cricket ball.
![]()
Question 2.
Define coefficient of viscosity. Explain Stoke’s law and explain the conditions under which a rain drop attains terminal velocity, υt. Give the expression for υt.
Answer:
Coefficient of viscosity (η): The coefficient of viscosity is defined as the tangential force per unit area of the layer, required to maintain unit velocity gradient.
η = \(\frac{F}{A\left(\frac{\Delta V}{\Delta x}\right)}\)
S.l. unit → Nm-2 s (or) PaS
C.G.S unit → Poise
Dimensional formula = [ML-1T-1]
Stoke’s law : According to this law the viscous force acting on a moving body which is spherical in shape is directly proportional to
- Coefficient of viscosity of fluid (η)
- Radius of the spherical body (r)
- Velocity of the body (v)
∴ F ∝ ηrv
F = Kηrv
Where K is a constant of proportionality. Experimentally it was found to be 6π.
∴ F = 6πηrv
When rain drops falling through air from the clouds reach the surface with almost constant speed through they are moving under gravitational force. This velocity is called terminal velocity. After attaining the terminal velocity, net force acting on the rain drop is zero.
According to stokes law, F ∝ ηrv
F = 6πηrv (∵ 6π = K = Proportionality constant)
Let ρ, r be the density and radius of the sphere.
The fluid density be σ.
The forces acting on the sphere are
- Weight of the sphere W = mg
W = Vρg = \(\frac{4}{3}\)πr3ρg …………….. (1) - The force of buoyancy (B) = V σ g = \(\frac{4}{3}\)πr3σg ……………. (2)
- Viscous force (f) = 6πηv ………………… (3)
When the sphere attains terminal velocity (vt), the net force on the body becomes zero.
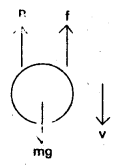
∴ At terminal velocity
Net downward force = Net upward force
W = B + f, W – B = f
\(\frac{4}{3}\)πr3ρg – \(\frac{4}{3}\)πr3σg = 6πηrvt;
∴ \(\frac{4}{3}\)πr3g (ρ – σ) = 6πηrvt
Vt = \(\frac{2}{9} \frac{r^2 g(\rho-\sigma)}{\eta}\) ………………. (4)
Problems
Question 1.
Calculate the work done in blowing a soap bubble of diameter 0.6 cm against the surface tension force. (Surface tension of soap solution = 2.5 × 102 Nm-1).
Solution:
D = 0.6 cm = 0.6 × 102 m
r = \(\frac{D}{2}=\frac{0.6 \times 10^{-2}}{2}\) = 0.3 × 102 m
S = 2.5 × 102 N/m
W = 8πr2s
= 8 × 3.14 × (0.3 × 10-2)2 × 2.5 × 10-2
W = 5.652 × 10-6 J
![]()
Question 2.
How high does methyl alcohol rise in a glass tube of diameter 0.06 cm ? (Surface tension of methyl alcohol = 0.023 Nm-1 and density = 0.8 gmcm-3. Assume that the angle of contact is zero)
Solution:
D = 0.06cm, θ = 0°
r = \(\frac{D}{2}=\frac{0.06}{2}\) = 0.03 cm = 0.03 × 10-2 m
= 3 × 10-4 m
S = 0.023 N/m, Density = 0.8 gm/c.c.
= 0.8 × \(\frac{10^{-3}}{10^{-6}}\)
ρ = 0.8 × 103 kg/m3
S = \(\frac{\mathrm{hr \rho g}}{2 \cos \theta}\)
h = \(\frac{2 \cos \theta}{r \rho g}\)
= \(\frac{2 \times 0.023}{3 \times 10^{-4} \times 0.8 \times 10^3 \times 9.8}\) (∵ cos 0° = 1)
= 0.0019 × 10-1 m
≈ 0.002 m
h = 2 cm .
Question 3.
What should be the radius of a capillay tube if water has to rise to a height pf 6 cm in it ? (Surface tension of water = 7.2 × 10-2 Nm-1).
Solution:
h = 6 × 10-2 m
S = 7.2 × 10-2 N/m
Density of water (ρ) = 103 kg/m3
S = \(\frac{\mathrm{hr \rho g}}{2}\)
r = \(\frac{2 \mathrm{~S}}{\mathrm{h \rho g}}=\frac{2 \times 7.2 \times 10^{-3}}{6 \times 10^{-2} \times 10^3 \times 9.8}\)
r = \(\frac{14.4}{58.8} \) × 10-3
r = 0.24 × 10-3 m
r = 0.24 mm
![]()
Question 4.
Find the depression of the meniscus in the capillary tube of diameter 0.4 mm dipped in a beaker containing , mercury. (Density of mercury = 13.6 × 103 Kg m-3 and surface tension of mercury = 0.49 Nm-1 and angle of contact = 135°).
Solution:
D = 4 m.m
r = \(\frac{D}{2}=\frac{4}{2}\) = 2m.m = 2 × 10-3 m
ρ = 13.6 × 103 kg/m3
θ = 135°, S = 0.49 Nm
cosθ = cos 135°
= – sin 45° = – \(\frac{1}{\sqrt{2}}\)
S = \(\frac{\mathrm{hr \rho g}}{2 \cos \theta}\)
h = \(\frac{2 \mathrm{~s} \cos \theta}{\mathrm{r \rho g}}\)
= 2 × 0.49 \(\left(\frac{-1}{\sqrt{2}}\right) \frac{1}{2 \times 10^{-3} \times 13.6 \times 10^3 \times 9.8}\)
h = \(\frac{-0.49}{13.6 \times 9.8 \times \sqrt{2}}\)
h = -0.024m.
Question 5.
If the diameter of a soap bubble is 10 mm and its surface tension is 0.04 Nm-1, find the excess pressure inside the bubble. [Mar. 14]
Solution:
D = 10 m.m
r = \(\frac{D}{2}=\frac{10}{2}\) = 5 m.m
= 5 × 10-3
S = 0.04 N/m
Pi – P0 = \(\frac{4 S}{r}=\frac{4 \times 0.04}{5 \times 10^{-3}}\)
= 0.032 × 103
Pi – P0 = 32 N/m2 (or) Pascal.
Question 6.
If work done by an agent to form a bubble of radius R is W, then how much energy is required to increase its radius to 2R ?
Solution:
R1 = R, R2 = 2R
Initial work done (W) = 8πR2S
Final work done (W) = 8π[R22 – R12]S
= 8π [4R2 – R2]S
= 3 × 8π R2S
W = 3W.
![]()
Question 7.
If two soap bubbles of radii R1 and R2 (in vacuum) coalasce under isothermal conditions, what is the radius of the new bubble. Take T as the surface tension of soap solution.
Solution:
R1, R2 and R be the radii of first, second and resultant bubble. The soap bubbles coalesce in vacuum, so surface energy do not change
E = E1 + E2
8π R2T = 8π R12T + 8π R22 T
R2 = R12 + R22
R = \(\sqrt{R_1^2+R_2^2}\)
Additional Problems
Question 1.
Explain why
a) The blood pressure in humans is greater at the feet than at the brain.
b) Atmospheric pressure at a height of about 6 km decreases to nearly half of its value at the sea level, though the height of the atmosphere is more than 100 km.
c) Hydrostatic pressure is a scalar quantities even though pressure is force divided by area.
Answer:
a) The height of the blood column in the human body is more at feet than at the brain. That is why, the blood exerts more pressure at the feet than at the brain (∴ pressure = hρg)
b) We know that the density of air is maximum near the surface of earth and decreases rapidly with height and at a height of about 6 km, it decreases to near by half its value at the sea level. Beyond 6 km height the density of air decreases very slowly with height. Due to this reason, the atmospheric pressure at a height of about 6 km decreases to nearby half of its value at sea level.
c) Since due to applied force on liquid, the pressure is transmitted equally in all directions inside the liquid. That is why there is no fixed direction for the pressure due to liquid. Hence hydrostatic pressure is a scalar quantity.
![]()
Question 2.
Explain why
a) The angle of contact of mercurywith glass is obtuse, while that of water with glass is acute.
b) Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.) [T.S. Mar. 15]
c) Surface tension of a liquid is independent of the area of the surface.
d) Water with detergent disolved in it should have small angles of contact.
e) A drop of liquid under no external forces is always spherical in shape.
Answer:
a) When a small quantity of liquid is poured on solid, three interfaces, namely liquid- air, solid-air and solid-liquid are formed. The surface tensions corresponding to these three interfaces are SLA, SSA and SSL respectively. Let 0 be the angle of contact between the liquid and solid. The molecules in the region, where the three interfaces meet are in equilibrium. It means net force acting on them is zero. For the molecule at 0 to be in equilibrium, we have.
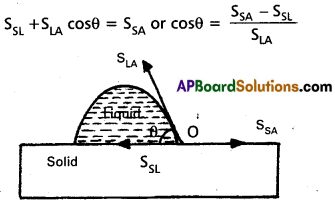
In case of mercury glass, SSA < SSL, therefore cosθ is negative or θ > 90° i.e. obtuse. In case of water-glass, SSA > SSL, therefore cosθ is positive or θ < 90° i,e. acute.
b) For mercury glass, angle of contact is obtuse. In order to achieve this obtuse value of angle of contact, the mercury tends to form a drop. In case of water glass, the angle of contact is acute. To achieve this acute value of angle of contact, the water tends to spread.
c) Surface tension of liquid is the force acting per unit length on a line drawn tangentially to the liquid surface at rest. Since this force is independent of the area of liquid surface, therefore surface tension is also independent of the area of the liquid surface.
d) We know that the cloth has narrow spaces in the form of capillaries. The rise of liquid in a capillary tude is directly proportional to cos0. if 0 is small cos0 will be large. Due to which capillary rise will be more and so the detergent will penetrate more in cloth.
e) In the absence of external forces, the surface of the liquid drop tends to acquire the minimum surface area due to surface tension. Since for a given volume, the surface area of sphere is least, hence the liquid drop takes the spherical shape.
Question 3.
Fill in the blanks using the word (S) from the list appended with each statement ;
a) Surface tension of liquids generally … with temperatures (increases / decreases)
b) Viscosity of gases… with temperature, whereas viscosity of liquids … with temperature (increases / decreases)
c) For solids with elastic modulus of rigidity, the shearing force is proportional to…. while for fluids it is proportional to … (shear strain / rate of shear strain)
d) For a fluid in a steady flow, the increase in flow speed at a constriction follows (conservation of mass / Bernoulli’s principle)
e) For the model of a plane in a wind tunnel, turbulence occurs at a… speed for turbulence for an actual plane (greater / smaller)
Answer:
a) Decreases
b) increases; decreases
c) Shear strain; rate of shear strain.
d) Conservation of mass; Bernoullis principle.
e) Greater.
![]()
Question 4.
Explain why
a) To keep a piece of paper horizontal, you should blow over, not under, it.
b) When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers.
c) The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection.
d) A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel.
e) A spinning cricket ball in air does not follow a parabolic trajectory.
Answer:
a) When we blow over the paper, the velocity of air blow increases and hence pressure of air on it decreases (according to Bernoullis theorem), whereas pressure of air below the paper is atmosphere. Hence the paper stays horizontal.
b) By doing so the area of the outlet of water jet is reduced, so velocity of water increases according to equation of continuity av = a constant.
c) When a fluid is flowing out of a small hole in a vessel it acquires a large velocity and hence possesses large momentum. Since no external force is acting on the system, a backward velocity must be attained by the vessel (according to law of conservation of momentum). As a result of it, impulse (backward thrust) is experienced by the vessel.
d) There, size of the needle controls velocity of flow and thumb pressure controls pressure. According to Bernoulli’s theorem, P + ρgh + \(\frac{1}{2}\) ρV2 = a constant shows that P occurs with power one and V occurs with power two, hence the velocity has more influence. That is why the needle has a better control over flow.
e) If the ball is spinning well as moving linearly, the streamlines at the top of ball due to two types of motion are opposed to each other and those below are in the same direction. As a result of it, the velocity of air flow is greater below than above the ball. Now, according to Bernoullis principle, the pressure on the upper side of the ball becomes more than the pressure on the lower side of ball. Due to it, a resultant force F acts upon the ball at right angle to linear motion in the downward, direction, resulting the ball to move along a curved path.
Question 5.
A 50 kg girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter 1.0 cm. What is the pressure exerted by the heel on the horizontal floor ?
Answer:
Here, m = 50kg; r =D/2 = 1/2 cm = \(\frac{1}{200}\) m
Pressure = \(\frac{\text { Force }}{\text { area }}=\frac{m g}{\pi r^2}=\frac{50 \times 9.8}{(22 / 7)(1 / 200)^2}\)
= 6.24 × 106 Nm-2.
![]()
Question 6.
Toricelli’s barometer used mercury. Pascal duplicated it using French wine of density 984 kg m-3. Determine the height of the wine column for normal atmosphere pressure.
Answer:
P = 0.76 × (13.6 × 103) × 9.8
= h × 984 × 9.8 or
h = \(\frac{0.76 \times 13.6 \times 10^3 \times 9.8}{984 \times 9.8}\)
= 10.5 m.
Question 7.
A vertical off-shore structure is built to withstand a maximum stress of 109 Pa. Is the structure suitable for putting up on top of an oil well in the ocean ? Take the depth of the ocean to be roughly 3 km and ignore ocean currents.
Answer:
Here, maximum stress = 109Pa,
h = 3km = 3 × 103m;
ρ(water) = 103kg/m3 and g = 9.8 m/s2
The structure will be suitable for putting upon top of an oil well provided the pressure exerted by sea water is less than the maximum stress it can bear.
Pressure due to sea water, P = hρg
= 3 × 103 × 103 × 9.8
= 2.94 × 107 Pa
Since the pressure of sea water is less than the maximum stress of 109 Pa, the structure will be suitable for putting upon top of the oil well.
Question 8.
A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm2. What maximum pressure would the smaller piston have to bear ?
Answer:
The maximum force, which the bigger piston can bear,
F = 3000 kgf = 3000 × 9.8 N
∴ Area of piston, A = 425 cm2
= 425 × 10-4 m2
∴ maximum pressure on the bigger piston.
P = \(\frac{F}{A}=\frac{3000 \times 9.8}{425 \times 10^{-4}}\) = 6.92 × 105 Pa
Since the liquid transmits pressure equally, therefore the maximum pressure the smaller piston can bear is 6.92 × 105 Pa.
![]()
Question 9.
A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0 cm of water in one arm and 12.5 cm of spirit in the other. What is the specific gravity of spirit ?
Answer:
For water column in one arm of U-tube,
h1 = 10.0 cm; ρ1 (density) = 1g cm-3
For spirit column in other arm of U-tube, h2 = 12.5 cm; ρ1 = ?
As the mercury column in the two arms of U-tube are in level, therefore pressure exerted by each is equal. Hence h1ρ1g = h2ρ2g or
P2 = \(\frac{h_1 \rho_1}{h_2}=\frac{10 \times 1}{12.5}\) = 0.8 g cm-3
Therefore, relative density of spirit = ρ2/ρ1
= \(\frac{0.8}{1}\) = 0.8
Question 10.
In the previous problem, if 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms ? (Specific, gravity of mercury = 13.6)
Answer:
On pouring 15.0 cm of water and spirit each into the respective arms of U-tube, the mercury level will rise in the arm containing spirit. Let h be the difference in the levels of mercury in two arms of U-tube and p be the density of mercury.
∴ The pressure exerted by h cm of mercury column = difference in pressure exerted by water and spirit.
∴ h1ρ1g = h2ρ2g ……………. (1)
Here h = ? ρ =13.6 g cm-3
ρ1 =1 cm-3
ρ2 = 0.8 g cm-3
h1 = 15 + 10 = 25 cm
h2 = 15 + 12.5 = 27.5 cm
Putting values in (i) we get h × 13.6 × g
= 25 × 1 × g – 27.5 × 0.8 × g = 3g
or h = 3/13.6 = 0.22cm
Question 11.
Can Bernoulli’s equation be used to describe the flow of water through a rapid in a river ? Explain.
Answer:
No, Bernoulli’s theorem is used only for stream – line flow.
![]()
Question 12.
Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation ? Explain.
Answer:
No, it does not matter if one uses gauge instead of absolute pressures in applying Bernoulli’s’ equation, provided the atmospheric pressure at the two points where Bernoulli’s equation is applied are significantly different.
Question 13.
Glycerine flows steadily through a horizontal tube of length 1.5 m and radius 1.0 cm. If the amount of glycerine collected per second at one end is 4.0 × 10-3 kg s-1, what is the pressure difference between the two ends of the tube ? (Density of glycerine = 1.3 × 103 kg m-3 and viscosity of glycerine = 0.83 Pa s). [You may also like to check if the assumption of laminar flow in the tube is correct].
Answer:
Here, l = 1.5 m, r = 1.0 cm = 10-2 m, ρ = 1; 1.3 × 10-3 kg/m3; η = 0.83 Nsm-2.
Mass of glycerine flouring per sec, M = 4 × 10-3 kg/s
Volume of glycerine flouring per sec, V = \(\frac{M}{\rho}\)
V = \(\frac{4 \times 10^{-3}}{1.3 \times 10^3} \mathrm{~m}^3 \mathrm{~s}^{-1}\) m3s-1
If ρ is the difference of pressure between two ends of the tube,then using poisevilles formula we have
V = \(\frac{\pi \rho r^4}{8 \eta l}\) or P = \(\frac{V \times 8 \eta l}{\pi r^4}\)
P = \(\left(\frac{4 \times 10^{-3}}{1.3 \times 10^3}\right) \times \frac{8 \times 0.83 \times 1.5}{3.142 \times\left(10^{-2}\right)^4}\)
= 975.37 Pa
Question 14.
In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70 m s-1 and 63 m s-1 respectively. What is the lift on the wing if its area is 2.5 m2 ? Take the density of air to be 1.3 kg m-3.
Answer:
Let V1, V2 be the speeds on the upper and lower surfaces of the wing of aeroplane and P1 and P2 be the pressures on upper and lower surfaces of the wing respectively.
Then V1 = 70ms-1; V2 = 63ms-1,
P = 1.3kg m-3.
This difference of pressure provides the lift to the aeroplane.
\(\frac{P_1}{\rho}\) + gh + \(\frac{1}{2} V_1^2\) = \(\frac{P_2}{\rho}\) + gh + \(\frac{1}{2} V_2^2\)
∴ \(\frac{P_1}{\rho}-\frac{P_2}{\rho}=\frac{1}{2}\left(V_2^2-V_1^2\right)\)
or P1 – P2 = \(\frac{1}{2} \rho\left(V_2^2-V_1^2\right)\)
= \(\frac{1}{2}\) × 1.3 [(70)2 – (63)2]
= 605.15 Pa
This difference of pressure provides the lift to the aeroplane.
So, lift on the aeroplane = Pressure difference × area of wings
= 605.15 × 2.5
= 1512.875 N
= 1.51 × 103N.
![]()
Question 15.
Figures (a) and (b) refer to the steady flow of a (non-viscous) liquid. Which of the two figures is incorrect ? Why ?
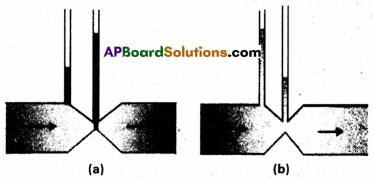
Answer:
Figure a is incorrect. According to equation of continuity i.e. av = a constant, where area of cross – section of tube is less, the velocity of liquid flow is more than the other portion of tube. According to Bernoulli’s theorem,
P + \(\frac{1}{2}\) ρv2 = a constant i.e. where V is more P is less and avice versa.
Question 16.
The cylindrical tube of a spray pump has a cross-section of 8.0 cm2 one end of which has 40 fine holes each of diameter 1.0 mm. If the liquid flow inside the tube is 1.5 m min-1, what is the speed of ejection of the liquid through the holes ?
Answer:
Area of cross – section of tube, a1 = 8.0 cm2 = 8 × 10-4 m2
No. of holes = 40, Diameter of each hole, D = 1 mm = 10-3 m
∴ Radius of hole, r = \(\frac{D}{2}=\frac{1}{2}\) × 10-3 m
= 5 × 10-4 m
Area of cross – section of each hole = πr2
= π(5 × 10-4)2m2
Total area of cross – section of 40 holes,
a2 = 40 × π (5 × 10-4)2m2
Speed of liquid inside the tube,
V1 = 1.5m/min
= \(\frac{1.5}{60}\) ms-1
If V2 is the velocity of ejection of the liquid through the holes, then
a1V1 = a2V2 or V2 = \(\frac{a_1 V_1}{a_2}\)
V2 = \(\frac{\left(8 \times 10^{-4}\right) \times 1.5}{60 \times 40 \times \pi \times\left(5 \times 10^4\right)^2}\)
= 0.637 ms-1
Question 17.
A U-shaped wire is dipped in a soap solution and removed. The thin shaped film formed between the surfaces and the light slider supports a weight of 1.5 × 10-2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film ?
Answer:
We know that soap film has two free surfaces, so total length of the film to be supported,
= 2l = 2 × 30 = 60 cm
= 0.6 m
Total force on the slider due to surface tension will be,
F = S × 2l
= S × 0.6 N
In equilibrium position, the force F on slider due to surface tension must balance the weight mg
(1.5 × 10-2)N i.e. F = 1.5 × 10-2
= S × 0.6 Or
S = \(\frac{1.5 \times 10^{-2}}{0.6}\)
2.5 × 10-2Nm-1
![]()
Question 18.
Figure (a) shows a thin liquid film supporting a small weight = 4.5 × 10-2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c) ? Explain your answer physically.
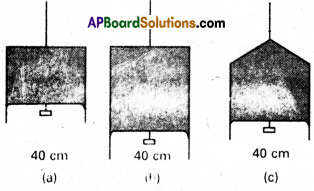
Answer:
a) Here, length of film supporting the weight
= 40cm = 0.4 m
Total liquid film supported (or force)
= 4.5 × 10-2 N
film has two free surfaces, ∴ surface tension,
S = \(\frac{4.5 \times 10^{-2}}{2 \times 0.4}\)
S = 5.625 × 10-2 Nm-1
Since the liquid is same for all the cases (a), (b), (c) and temperature is also same, therefore surface tension for cases (b) and (c) will also be the same = 5.625 × 10-2. In figure (b) and (c) the length of the film supporting the weight is also the same as that of(a), hence the total weight supported in each case is 4.5 × 10-2 N.
Question 19.
What is the pressure inside the drop of mercury of radius 3.00 mm at room temperature ? Surface tension of mercury at that temperature (20°C) is 4.65 × 10-1 Nm-1. The atmospheric pressure is 1.01 × 105 Pa. Also give the excess pressure inside the drop.
Answer:
Here, r = 3.0 mm = 3 × 10-3 m;
S = 4.65 × 10-1 Nm-1;
P = 1.01 × 105 Pa
Excess of pressure inside the drop of mercury is given by
P = \(\frac{2 S}{r}=\frac{2 \times 4.65 \times 10^{-1}}{3 \times 10^{-3}}\)
= 310 Pa
Total pressure inside the drop = P + ρ
= 1.01 × 105 + 310
= 1.01 31 × 105 Pa
Question 20.
What is the excess pressure inside a bubble of soap solution of radius 5.0 mm, given that the surface tension of soap solution at the temperature (20°C) is 2.50 × 10-2 Nm-1? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble ? (1 atmospheric pressure is 1.01 × 105 Pa).
Answer:
Here, S = 2.5 × 10-2 Nm-1, r = 5.00 mm = 5 × 10-3 m.
Density of soap solution, ρ = 1.2 × 103 kg m-3
Excess pressure inside the soap bubble,
P = \(\frac{4 s}{r}=\frac{4 \times 2.5 \times 10^{-2}}{5 \times 10^{-3}}\) = 20 Pa
Excess pressure inside the air bubble, P’ = \(\frac{2S}{r}\)
= \(\frac{2 \times 2.5 \times 10^{-2}}{5 \times 10^{-3}}\) = 10 Pa
Total pressure inside the air bubble at depth h in soap solution – ρ’ + atmospheric pressure + hρg
= 10 + 1.01 × 105 + 0.4 × 1.2 × 103 × 9.8
= 1.06 × 103 Pa
![]()
Question 21.
A tank with a square base of area 1.0 m2 is divided by a vertical partition in the middle. The bottom of the partition has a small-hinged door of area 20 cm2. The tank is filled with water in one compartment and an acid (of relative density 1.7) in the other, both to a height of 4.0 m. compute the force necessary to keep the door close.
Answer:
For compartment containing water,
h1 = 4m, ρ1 = 103 kg m-3
The pressure exerted by water at the door provided at bottom
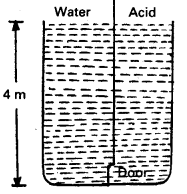
P1 = h1ρ1g
= 4 × 103 × 9.8
= 3.92 × 104 Pa
For compartment containing acid,
h2 = 4m,
ρ2 = 1.7 × 1.03 kg/m3
The pressure exerted by acid at the door provided at bottom.
P2 = h2ρ2g
= 4 × 1.7 × 103 × 9.8
= 6.664 × 104 Pa
∴ Difference of pressure = P2P1
= 6.664 × 104 – 3.92 × 104
= 2.774 × 104Pa
Given, area of door, A = 20cm2
= 20 × 10-4m2
Force on the door = difference in pressure × area
= (P2 – P1) × A
= (2.774 × 104) × (20 × 104)
= 54.88N
≈ 55N
To keep the door closed, the force equal to 55 N should be applied horizontally on the door from compartment containing water to that containing acid.
Question 22.
A manometer reads the pressure of a gas in an enclosure as shown in Fig. (a) when a pump removes some of the gas, the manometer reads as in Fig. (b) The liquid used in the manometers is mercury and the atmo-spheric pressure is 76 cm of mercury.
a) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and b) in units of cm of mercury.
b) How would the levels change in case (b) if 13.6 cm of water (immiscible with mercury, are poured into the right limb of the manometer? (Ignore the small change in the volume of the gas).
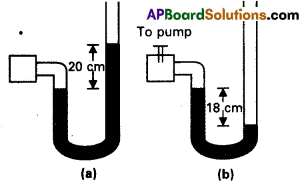
Answer:
a) Here, atomospheric presure, p = 76 cm of mercury
In Fig (a) Pressure head
h = + 20 cm
∴ Absolute pressure = p + h
= 76 + 20
= 96 cm of mercury
Gauge pressure = h = 20 cm of mercury.
In fig (b) pressure head, h = -18 cm
Absolute pressure = p + h
= 76+ (-18)
= 58 cm of mercury
Gauge pressure = h = -18cm of mercury.
b) Here 13.6 cm of water added in right limb is equiralent to
\(\frac{13.6}{13.6}\) = 1 cm of mercury column.
i.e., h1 = 1 cm of mercury column.
Now pressure at A, PA = P + h1 = 76 + 1
= 77 cm
Let the difference in mercury levels in the two lumbs be h1, then pressure at B,
PB = 58 + h1 or
As PA = PB = 77 = 58 + h1
h1 = 77 – 58 = 19 cm of mercury column.
![]()
Question 23.
Two vessels have the same base area but different shapes. The first vessel takes twice the volume of water that the second vessel requires to fill upto a particular comon height. Is the force exerted by the water on the base of the vessel the same in the two cases ? If so, why do the vessels filled with water to that same height give different readings on a weighing scale ?
Answer:
Since the pressure depends upon the height of water column and the height of the water column in the two vessels of different shapes is the same.hence there will be same pressure due to water on the base of each vessel. As the base area of each vessel is same, hence there will be equal force acting on the two base areas due to water pressure. The water exerts force on the walls of the vessel also. In case, the walls of the vessel are not perpendicular to base, the force exerted by water on the walls has a net non-zero vertical component which is more in first vessel than that of second vessel. That is why, the two vessel:; filled with water to same vertical height show different readings on a weighing machine.
Question 24.
During blood transfusion the needle is inserted in a vein where the gauge pressure is 2000 Pa. At what height must the blood container be placed so that blood may just enter the vein ? Use the density of whole blood from Table 1.
Answer:
h = \(\frac{p}{p g}=\frac{200}{1.06 \times 10^3}\) × 9.8 = 0.1925 m
The blood may just enter the vein if the height at which the blood container be kept must be slightly greater than 0.1925 m i.e. 0.2 m.
Question 25.
In deriving Bernoulli’s equation, we equated the work done on the fluid in the tube to its change in the potential and kinetic energy.
a) What is the largest average velocity of blood flow in an artery of diameter 2 × 10-3 m if the flow must remain laminar ?
b) Do the dissipative forces become more important as the fluid velocity increases ? Discuss qualitatively.
Answer:
a) If dissipative forces are present, then some forces in liquid flow due to pressure different is spent against dissipative forces. Due to which the pressure drop becomes large.
b) The dissipative forces become more important with increasing flow velocity, because of tubulence.
![]()
Question 26.
a) What is the largest average velocity of blood flow in an artery of radius 2 × 10-3m if the flow must remain lanimar ?
Answer:
Here, r = 2 × 10-3m ;
D = 2r = 2 × 2 × 10-3 = 4 × 10-3m
η = 2.084 × 10-3 Pa s;
p = 1.06 × 103 kgm3
For flow tobe laminar, Nr = 2000
a) Now, Vc = \(\frac{N_r \eta}{\rho D}\)
= \(\frac{2000 \times\left(2.084 \times 10^{-3}\right)}{\left(1.06 \times 10^3\right) \times\left(4 \times 10^{-3}\right)}\) = 0.98m/s.
b) What is the corresponding flow rate ? (Take viscosity of blood to be 2.084 × 10-3 Pa s).
Answer:
Volume flowing per second = πr2Vc
= \(\frac{22}{7}\) × (2 × 10-3)2 × 0.98
= 1.23 × 10-5 m3s-1
Question 27.
A plane is in level flight at constant speed and each of its two wings has an area of 25m2. If the speed of the air is 180 km/h over the lower wing and 234 km/h over the upper wing surface, determine the plane’s mass. (Take air density to be 1 kg m-3)
Answer:
Here, V1 = 180 km/h = 50m/s, V2 = 234 km/ h = 65 m/s;
A = 2 × 25 = 50m2; P = 1kg/m3
P1 – P2 = \(\frac{1}{2}\) p (V22 – V12)
= \(\frac{1}{2}\) × 1 × (652 – 502)
Upward force = (P1 – P2) A = \(\frac{1}{2}\) × (652 – 502) × 50N
As the plane is in level flight, so
mg = (P1 – P2)A
or m = \(\frac{\left(P_1-P_2\right) A}{g}=\frac{1 \times\left(65^2-50^2\right) \times 50}{2 \times 9.8}\)
= 4.4 × 103N
Question 28.
In Millikan’s oil drop experiment, what is the terminal speed of an uncharged drop of radius 2.0 × 10-5 m and density 1.2 × 103 kg m-3. Take the viscosity of air at the temperature of the experiment to be 1.8 × 105 Pa s. How much is the viscous force on the drop at that speed ? Neglect buoyancy of the drop due to air.
Answer:
Here, r = 2.0 × 10-5m; ρ = 1.2 × 103 kg m-3;
η = 1.8 × 105 Ns m-2
P0 = 0, V = ?, F = ?
Terminal velocity V = \(\frac{2 r^2\left(\rho-\rho_0\right) g}{9 \eta}\)
= \(\frac{2 \times\left(2.0 \times 10^{-5}\right)^2 \times\left(1.2 \times 10^3-0\right) \times 9.8}{9 \times 1.8 \times 10^{-5}}\)
= 5.8 × 10-2ms-1 = 5.8 cms-1
Viscous force on the drop, F = 6πηrv
= 6 × \(\frac{22}{7}\) × (1.8 × 10-5) × (2.0 × 10-5) × (5.8 × 10-2)
= 3.93 × 10-10N.
![]()
Question 29.
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside ? Surface tension of mercury at the temperature of the experiment is 0.456 N m-1. Density of mercury = 1.36 × 103 kg m-3.
Answer:
Here, θ = 140°, r = 1 × 10-3 m;
S = 0.465 Nm-1, ρ = 13.6 × 103 kg, h = ?]
Cos = 140° = – cos40° = -0.7660
Now h = \(\frac{2 S \cos \theta}{r \rho g}\)
= \(\frac{2 \times 0.465 \times \cos 140^{\circ}}{10^{-3} \times 13.6 \times 10^3 \times 9.8}\)
= \(\frac{2 \times 0.465 \times(-0.7660)}{10^{-3} \times 13.6 \times 10^3 \times 9.8}\)
= -5.34 × 10-3m
= -5.34mm
Negative value of h shows that the mercury levels is depressed in the tube.
Question 30.
Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to forma a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube ? Surface tension of water at the temperature of the experiment is 7.3 × 10-2 N m-1. Take the angle of contact to be zero and density of water to be 1.0 × 103 kg m-3 (g = 9.8 m-2).
Answer:
Here, S = 7.3 -2 Nm-1, ρ = 1.0 × 103 kg m-3; θ = 0°
For narrow tube, 2r1 = 3.00 mm = 3 × 10-3 m or r1 =1.5 × 10-3 m .
For wider tube, 2r2 = 6.00 mm = 6 × 10-3 m or r2 = 3 × 10-3 m
let h1, h2 be the heights to which water rises in narrow tube and wider tube respectively.
Then, h1 = \(\frac{2 s \cos \theta}{r_1 \rho g}\) and h2 = \(\frac{2 s \cos \theta}{r_2 \rho g}\)
∴ Difference in levels of water in two limbs of U-tube is
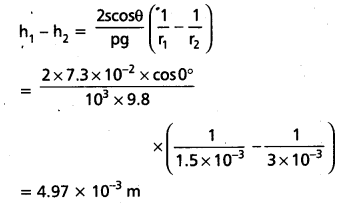
Question 31.
a) It is known that density of air decreases with height y as
ρ = ρ0e-y/y0
Where p0 = 1.25 kg m-3 is the density at sea level, and y0 is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant.
Answer:
We know that the rate of decrease of density p of air is directly proportional to height y i.e.
\(\frac{-d \rho}{d y}\) ∝ p or \(\frac{d \rho}{d y}\) = – Kρ
Where K is a constant of proportionality. Here – ve sign shows that ρ decreases as y increases.
\(\frac{d y}{\rho}\) = – Kρ
Integrating it with in the conditions, as y changes fromotoy density changes from ρ0 to ρ, we have
\(\left.\int_{P_0}^p \frac{d P}{P}=-\int_0^y k d y=\left[\log e^p\right)\right]_{\rho_0}^p=k y\)
\(\frac{\rho}{\rho_0}=e^{-k y}=\rho=\rho_0 e^{-\mathrm{y} / y_0}\)
b) A large He balloon of volume 1425 m3 is used to lift a payload of 400 kg. Assum that the balloon maintains constant radius as it rises. How high does it rise ?
(Take y0 = 8000 m and PHe = 0.18 kgm-3)
Answer:
The balloon will rise to aheight, where its density becomes equal to the air at that height.

y = 8000 × 1 = 8000 m
= 8 km.
Textual Examples
Question 1.
The two thigh bones (femurs), each of cross-sectional area 10 cm2 mass 40 kg. Estimate the average pressure sustained by the femurs.
Answer:
Total cross-sectional area of the femurs is A = 2 × 10 cm2 20 × 10-4 m2. The force acting on them is F = 40 kg wt = 400 N (taking g 10 ms-2). This force is acting vertically down and hence, normally on the femurs. Thus, the average pressure is
Pav = \(\frac{F}{A}\) = 2 × 105 N m-2
![]()
Question 2.
What is the pressure on a swimmer 10m below the surface of a lake ?
Answer:
Here
h = 10 m and p = 1000 kg m-3.
Take g 10 m S-2
From Equation = P = Pa + ρgh
P = Pa + ρgh
= 1.01 × 105 Pa + 1000 kgm-3 × 10m S-2 × 10 m
= 2.10 × 105 Pa
≈ 2 atm
This is a 100% increase in pressure from surface level. At a depth of 1 km the increase in pressure is 100 atm! Submarines are designed to withstand such enormous pressures.
Question 3.
The density of the atmosphere at sea level is 1.29 kg/m3. Assume that it does not change with altitude. Then how high would the atmosphee extend ?
Answer:
We use P – Pa = ρgh
ρgh = 1.29 kg m-3 × 9.8 ms2 × hm
= 1.01 × 105 pa
∴ h = 7989 m ≈ 8 km
In reality the density of air decreases with height. So does the value of g. The atmospheric cover extends with decreasing press-ure over 100 km. We should also note that the sea level atmospheric pressure is not always 760 mm of Hg. A drop in the Hg level by 10 mm or more is a sign of an approaching storm.
![]()
Question 4.
At a depth of 1000 m in an ocean
(a) What is the absolute pressure ?
b) What is the guage Pressure ?
c) Find the force acting on the window of area 20 cm × 20 cm of a submarine at this depth, the interior of which is maintained at sealevel atmospheric pressure. (The density of sea water is 1.03 × 103 kg m-3, g = 10ms-2.
Answer:
Here h = 1000 m and ρ = 1.03 × 103 kg m-3
a) From P2 – P1 = ρgh absolute pressure
P = Pa + ρgh
= 1.01 × 105 Pa + 1.03 × 103 kg m-3 × 10 m s-2 × 1000 m
= 104.01 × 105 Pa .
= 104 atm
b) Gauge pressure is P – Pa = ρgh = Pg
Pg = 1.03 × 103 kg m-3 × 10 m s2 × 1000 m
= 103 × 105 Pa
≈ 103 atm
c) The pressure outside the submarine is P = Pa + ρgh and the pressure inside it is Pa. Hence, the net pressure acting on the window is gauge pressure, Pg = ρgh. Since the area of the window is A = 0.04 m2, the force acting on it is
F = PgA = 103 × 105 Pa × 0.04m2
= 4.12 × 105 N
≈ 103 atm
Question 5.
Two syringes of different cross sections A1, A2 and lengths L1, L2 (without needles) filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston and larger piston are 1.0 cm and 3.0 cm respectively.
a) Find the force exerted on the larger piston when a force of ION is applied to the smaller piston, b) if the smaller piston is pushed in through 6.0 cm,’how much does the larger piston move out ?
Answer:
a) Since pressure is transmitted undiminished throughout the fluid.
F2 = \(\frac{A_2}{A_1} F_1=\frac{\pi\left(3 / 2 \times 10^{-2} m\right)^2}{\pi\left(1 / 2 \times 10^{-2} \mathrm{~m}\right)^2} \times 10 \mathrm{~N}\)
= 90 N
b) Water is considered to be perfectly incompressible. Volume covered by the move-ment of smaller piston inwards is equal to volume moved outwards due to the larger piston.
L1A1 = L2A2
L2 = \(\frac{A_1}{A_2} L_1=\frac{\pi\left(1 / 2 \times 10^{-2} \mathrm{~m}\right)^2}{\pi\left(3 / 2 \times 10^{-2} \mathrm{~m}\right)^2}\)
= × 6 × 10-2m
≃ 0.67 × 10-2m = 0.67 cm.
Note, atmospheric pressure is common to both pistons and has been ignored.
![]()
Question 6.
In a car lift compressed air exerts a force F1 on a small piston having a radius of 5.0 cm. This pressure is transmitted to a second piston or radius 15 cm (Fig). If the mass of the car to be lifted is 1350 kg, calculate F1. What is the pressure necessary to accomplish this task ? (g = 9.8 ms-2).
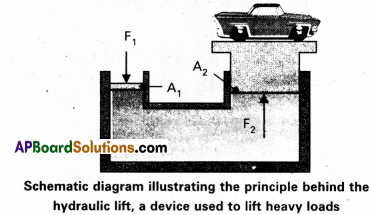
Answer:
Since pressure is transmitted undiminished throughout the fluid.
F1 = \(\frac{A_1}{A_2} F_2=\frac{\pi\left(5 \times 10^{-2} \mathrm{~m}\right)^2}{\pi\left(15 \times 10^{-2} \mathrm{~m}\right)^2}\)
= (1350 N × 9.8m s-2) = 1470 N
= 1.5 × 103N
The air pressure that will produce this force is
P = \(\frac{F_1}{A_1}=\frac{1.5 \times 10^{-3} \mathrm{~N}}{p\left(5 \times 10^{-2}\right)^2 \mathrm{~m}}\) = 1.9 × 105 Pa
This is almost double the atmospheric pressure.
Question 7.
Blooc velocity : The flow of blood in a large artery of an anesthetised dog is diverted through a Venturi meter. The wider part of the meter has a cross-sectional area equal to that of the artery. A = 8 mm2. The harrower part has an area = 4mn2. The pressure drop in the artery is 24 Pa. What is the speed of the blood in the artery ?
Answer:
We take the density of blood from whole blood to be 1.06 × 103 kg m3. The ratio of the areas is \(\left(\frac{\mathrm{A}}{\mathrm{a}}\right)\) = 2
Using v1 = \(\left(\sqrt{\frac{2 \rho_m g h}{\rho}}\right)\left(\left(\frac{A}{2}\right)^2-1\right)^{-1 / 2}\)
we obtain
v1 = \(\sqrt{\frac{2 \times 24 \mathrm{pA}}{1060 \mathrm{~kg} \mathrm{~m}^{-3} \times\left(2^2-1\right)}=0.125 \mathrm{~m} \mathrm{~s}^{-1}}\)
![]()
Question 8.
A fully loaded Boeing aircraft has a mass of 3.3 × 105 kg. Its total wing area is 500 m2. It is in level flight with a speed of 960 km/h. a) Estimate the pressure difference between the lower and upper surfaces of the wings (b) Estimate the fractional increase in the speed of the air on the upper surface of the wing relative to the lower surface. [The density of air is ρ = 1.2 kgm-3].
Answer:
a) The weight of’the Boeing aircraft is balanced by the upward force due to the pressure difference
∆P × A – 3.3 × 105 kg × 9.8 = mg.
∆P = (3.3 × 105 kg × 9.8 m s-2) / 500 m2
= 6.6 × 103 N m-2
b) We ignore the small height difference between the top and bottom sides in
P1 + (\(\frac{1}{2}\)) ρv12 + ρgh1 = P2 + (\(\frac{1}{2}\))ρv22 + ρgh2
The pressure difference between them is then
∆P = \(\frac{\rho}{2}\left(v_2^2-v_1^2\right)\)
Where v2 is the speed of air over the upper surface and v1 is the speed under the bottom surface.
(v2 – v1) = \(\frac{2 \Delta P}{\rho\left(v_2+v_1\right)}\)
Taking the average speed vav (v2 + v1)/2 – 960 km/h = 267 m s-1, we have
(v2 – v1)/vav = \(\frac{\Delta \mathrm{P}}{\rho v_{\mathrm{av}}^2}\) ≈ 0.08
The speed of air above the wing needs to be only 8% higher than that below.
Question 9.
A metal block of area 0.10 m2 is connected to a 0.010 kg mass via a string that passes over an ideal pulley (considered massless and frictionless), as in Fig. A liquid with a film thickness of 0.30 mm is placed between the block and the table. When released, the block moves to the right with a constant speed of 0.085 ms-1. Find the co-efficient of viscosity of the liquid.
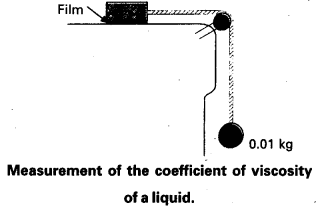
Answer:
The metal block moves to the right because of the tension in the string. The tension T is equal in magnitude to the weight of the suspended mass m. Thus the shear force F is
F = T = mg = 0.010 kg × 9.8 ms-2
= 9.8 × 10-2 N
Shear stress on the fluid = F/A = \(\frac{9.8 \times 10^{-2}}{0.10}\)
Strain rate = \(\frac{v}{l}=\frac{0.085 \mathrm{~ms}^{-1}}{0.3 \times 10^{-3} \mathrm{~m}}\)
η = \(\frac{\text { stress }}{\text { strain rate }}\)
= \(\frac{\left(9.8 \times 10^{-2} \mathrm{~N}\right)\left(0.30 \times 10^{-3} \mathrm{~m}\right)}{\left(0.085 \mathrm{~ms}^{-1}\right)\left(0.10 \mathrm{~m}^2\right)}\)
= 3.45 × 10-3 Pa s
![]()
Question 10.
The terminal velocity of a copper ball of radius 2.0 mm falling through a tank of oil at 20°C is 6.5 cm s-1. Compute the viscosity of the oil at 20°C. Density of oil is 1.5 × 103 kg m-3, density of copper is 8.9 × 103 kg m-3.
Answer:
We have vt = 6.5 × 10-2 ms-1,
a = 2 × 10-3m,
g = 9.8 ms-2, ρ = 8.9 × 103 kg m-3,
σ = 1.5 × 103 kg m-3. From
vt = \(\frac{2 a^2(\rho-\sigma) g}{(9 \eta)}\)
η = \(\frac{2}{9} \times \frac{\left(2 \times 10^{-3}\right) \mathrm{m}^2 \times 9.8 \mathrm{~ms}^{-2}}{6.5 \times 10^{-2} \mathrm{~ms}^{-1}}\) × 7.4 × 103 kg m-3
= 9.9 × 10-1 kg m-1s-1
Question 11.
a) The flow rate of water from a tap of diameter 1.25 cm is L7min. The co-efficient of viscosity of water is 10-3 Pa s.
b) After sometime the flow rate is increased to 3L / min. Characterise the flow for both the flow rates.
Answer:
a) Let the speed of the flow be v and the diameter of the tap be d = 1.25 cm. The volume of the water flowing out per second is
Q = v × π d2/4
v = 4Q / d2 π
We then estimate the Reynolds number to be
Re = 4vQ / πdη
= 4 × 103 kg m-3 × Q / (3.14 × 1.25 × 10-2 m × 10-3 Pa S)
= 1.019 × 108 m-3 SQ
Since initially (a)
Q = 0.48 L/min = 8cm3/s
= 8 × 10-6 m3 s-1, we obtain,
Re = 815
Since this is below 1000, the flow is steady.
After some time
b) When Q = 3L/ min = 50 cm3, s = 5 × 10-5 m3 s-1 we obtain,
Re = 5095
The flow will be turbulent. You may carry out an experiment in your washbasin to determine the ransition from laminar to turbulent flow.
![]()
Question 12.
The lower end of a capillary tube of diameter 2.00 mm is dipped 8.00 cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water ? The surface tension of water at temperature of the experiments is 7.30 × 10-2 Nm1. 1 atmospheric pressure = 1.01 × 105 Pa, density of water = 1000 kg/m3, g = 9.8 × ms-2. Also calculate the excess pressure.
Answer:
The excess pressure in a bubble of gas in a liquid is given by 2S / r, where S is the surface tension of the liquid gas interface. You should note there is only one liquid surface in this case. (For a bubble of liquid in a gas, there are two liquid surfaces, so the formula for excess pressure in that case is 4S / r.) The radius of the bubble is r. Now the pressure outside the bubble, within water, P0 equals atmospheric pressure plus the pressure due to 8.00 cm of water column. That is
P0 = (1.01 × 105 Pa + 0.08 m × 1000 kg m-3 × 9.80 m s-2)
= 1.01784 × 105 Pa. .
Therefore, the pressure inside the bubble is
P1 = P0 + 2S / r (as r = 1 mm)
= 1.01784 × 105 Pa + (2 × 7.3 × 10-2 Pa m/10-3 m)
= (1.01784 + 0.00146) × 105 Pa
= 1.02 × 105 Pa
where the radius of the bubble is taken to be equal to the radius of the capillary tube, since the bubble is hemispherical ! (The answer has been rounded off to three significant figures). The excess pressure in the bubble is 146 Pa from (1.0178 + 0.00146) × 105 Pa.