AP Inter 1st Year Chemistry Study Material Chapter 4 States of Matter: Gases and Liquids

Andhra Pradesh BIEAP AP Inter 1st Year Chemistry Study Material 4th Lesson States of Matter: Gases and Liquids Textbook Questions and Answers.

AP Inter 1st Year Chemistry Study Material 4th Lesson States of Matter: Gases and Liquids

Very Short Answer Questions

Question 1.
Name the different intermolecular forces experienced by the molecules of a gas.
Answer:
The different intermolecular forces experienced by the molecules of a gas are London (or) dispersion forces, Dipole-Dipole forces, Dipole- induced dipole forces, and hydrogen bonds.

Question 2.
State Boyle’s law. Give its mathematical expression.
Answer:
At constant temperature, the pressure of a given mass (fixed amount) of gas varies inversely with its volume. This is Boyle’s law.

• Mathematically it can be written as
  P ∝ \(\frac{1}{v}\) (At constant T and no.of moles (n))
  ⇒ Pv = \(\frac{k}{v}\) (constant).

Question 3.
State Charle’s law. Give its mathematical expression.
Answer:
At constant pressure the volume of a fixed mass of a gas is directly proportional to it’s absolute temperature. This is charle’s law.

• Mathematically it can be written as
  V ∝ T (At constant P and no.of moles (n))
  ⇒ V = kT
  ⇒ \(\frac{V}{T}\) = k (constant).

Question 4.
What are Isotherms?
Answer:
At constant temperature the curves which shows the relationship between variation of volume of a given mass of gas and pressure are called isotherms.

Question 5.
What is Absolute Temperature?
Answer:
It is also called thermodynamic temperature (or) Kelvin temperature. It is a temperature on the absolute (or) kelvin scale in which zero lies at – 273.16°C.
T = (t° C + 273.16) K

Question 6.
What are Isobars?
Answer:
The curves (or) graphs that can be drawn at constant pressure are called Isobars.
Eg : Graph drawn between volume and temperature.

Question 7.
What is Absolute Zero?
Answer:
It is the lowest temperature theoretically possible at which volume of a perfect gas is zero.

Question 8.
State Avogadro’s law.
Answer:
Equal volumes of all gases under the same conditions of temperature and pressure contains equal number of molecules
V ∝ n (mathematically)
v = kn

Question 9.
What are Isochores ?
Answer:
At constant volume a line on a graph showing the variation of temperature of a gas with its pressure is called Isochores.

• It is also called Isoplere.

Question 10.
What are S T P Conditions ?
Answer:
STP means Standard Temperature and Pressure conditions.

• Standard temperature is 0° C = 273 K
• Standard pressure is 1 atmosphere = 76 cm = 760 mm. of Hg.

At S.T.P. one mole of any gas occupy 22.4 lit. of volume.

Question 11.
What is Gram molar Volume ?
Answer:
The volume occupied by one gram molecular weight (or) one gram mole of an element (or) compound in the gaseous state is called gram molar volume.
(or)

• At STP one mole of any gas occupy 22.4 lit. of volume This is known as gram molar volume.

Question 12.
What is an Ideal gas ?
Answer:
A gas which obeys gas laws i.e. Boyle’s law, charle’s law and avagadro’s law exactly at all temperatures is called an ideal gas.

Question 13.
Why the gas constant ‘R’ is called Universal gas constant ?
Answer:
Gas constant ‘R’ is called universal gas constant because the value of ‘R‘ is same for all gases.

Question 14.
Why Ideal gas equation is called Equation of State ?
Answer:
Ideal gas equation is a relation between four variables (p, v, n, T) and it describes the state of any gas. Hence it is called equation of state.

Question 15.
Give the values of gas constant in different units.
Answer:
Gas constant ‘R’ has values in different units as follows.
R = 0.0821 lit. atm. k^-1 mol^-1
= 8.314 J. k^-1 mol^-1
= 1.987 (or) 2 cal. k^-1 mol^-1
= 8.314 × 10⁷ ergs. k^-1 mol^-1.

Question 16.
How are the density and molar mass of a gas related?
Answer:
Pv = n RT
Pv = \(\frac{w}{m}\) RT m
P = \(\left(\frac{w}{v}\right) \frac{R T}{M}\)
Molar mass M = \(\frac{\mathrm{dRT}}{\mathrm{P}}\) [∴ \(\frac{w}{v}\) = density(d)]
P = Pressure of gas
R = Universal gas constant
T = Temperature of gas in kelvins scale.

Question 17.
State Graham’s law of diffusion. (A.P. Mar. ‘16, ’14)
Answer:
The rate of diffusion of a given mass of gas at a given pressure and temperature is inversely proportional to the square root of its density
rate of diffusion r ∝ \(\frac{1}{\sqrt{d}}\).

Question 18.
Which of the gases diffuses faster among N₂, O₂ and CH₄? Why? (T.S. Mar. ‘15)
Answer:
CH₄ gas diffuse faster among N₂, O₂ and CH₄.
Reason : CH₄ (16) has low molecular weight than N₂ (28) and O₂ (32).

Question 19.
How many times methane diffuses faster than sulphurdioxide?
Answer:
According to Graham’s law of diffusion.

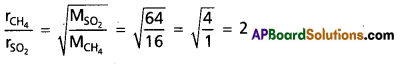
Hence methane gas diffuses 2 times faster than SO₂.

Question 20.
State Dalton’s law of Partial pressures. (Mar. ‘14)
Answer:
The total pressure exerted by a mixture of chemically non – reacting gases at given temperature and volume, is equal to the sum of partial pressures of the component gases.
P = P₁ + P₂ + P₃.

Question 21.
Give the relation between the partial pressure of a gas and its mole fraction.
Answer:
Partial pressure of a gas = mole fraction of the gas × Total pressure of the mixture of gases
Eg : Consider A and B in a container which are chemically non reaction.
∴ Partial pressure of A (P_A) = X_A × P_T
Partial pressure of B (P_B) = X_B × P_T
X_A = \(\frac{n_A}{n_A+n_B}\), X_B = \(\frac{n_B}{n_A+n_B}\)
X_A, X_B are mole fractions
P_T = Total pressure.

Question 22.
What is aqueous tension?
Answer:
The pressure exerted by the water vapour which is equilibrium with liquid water is called aqueous tension.
(or)
The pressure exerted by the saturated water vapour is called aqueous tension.

Question 23.
Give the two assumptions of Kinetic molecular theory of gases that do not hold good in explaining the deviation of real gases from ideal behaviour.
Answer:
The two assumptions of kinetic molecular theory of gases that do not hold good in explaining the deviation of real gases from ideal behaviour are

1. There is no force of attraction between the molecules of a gas.
2. Volume of the gas molecules is negligible when compared to the space occupied by the gas.

Question 24.
Give the Kinetic gas equation and write the terms in it.
Answer:
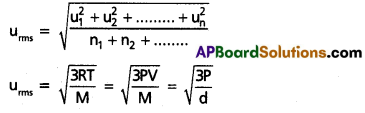
Kinetic gas equation is PV = \(\frac{1}{3} \mathrm{mnu}_{\mathrm{rms}}^2\)
P = Pressure of the gas
V = Volume of the gas
m = Mass of 1 mole of the gas
u_rms = RMS speed of the gas molecules.

Question 25.
Give an equation to calculate the kinetic energy of gas molecules.
Answer:
Kinetic energy for ‘n1 moles of gas is given by
K.E. = \(\frac{3}{2} \mathrm{nRT}\)
R = Universal gas constant
T = absolute temperature.

Question 26.
What is Boltzman’s constant ? Give its value.
Answer:
Boltzman’s constant is the gas constant per molecule.
Boltzman’s constant K = \(\frac{R}{N}\)
= 1.38 × 10^-16 erg/k. molecule
= 1.38 × 10^-23 J/k. molecule.

Question 27.
What is RMS speed ?
Answer:
The square root of mean of the squares of the speeds of all molecules of a gas is known as RMS speed (u_RMS)

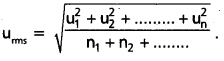
Question 28.
What is Average speed ?
Answer:
The arithematic mean of speeds of gas molecules is known as average speed (u_av).

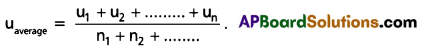
Question 29.
What is Most probable speed ?
Answer:
The speed possessed by the maximum number of molecules of the gas is known as most probable sPeed (u_mp).

Question 30.
What is the effect of temperature on the speeds of the gas molecules ?
Answer:
Temperature and speeds of the gases are directly related.
∴ By the rise of temperature the speeds of the gas molecules also increases.

Question 31.
What is the effect of temperature on the kinetic energy of the gas molecules ?
Answer:
According to the postulates of kinetic molecular theory of gases.
The kinetic energy of gas molecules is directly proportional to the absolute temperature.
K.E. ∝ T_abs

Question 32.
Give the ratio of RMS average and most probable speeds of gas molecules.
Solution:

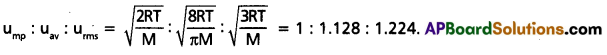
Question 33.
Why RMS speed is taken in the derivation of Kinetic gas equation ?
Answer:
RMS speed is the mean of squares of speeds of all molecules of gas. Hence RMS speed, is taken into the derivation of kinetic gas equation.
PV = \(\frac{1}{3} m n u_{r m s}^2\)

Question 34.
What is Compressibility factor ?
Answer:
The ratio of the actual molar volume of a gas to the molar volume of a perfect gas under the same conditions is called compressibility factor.
Compressibility factor Z = \(\frac{\mathrm{PV}}{\mathrm{nRT}}\)
For a perfect gas Z = 1.

Question 35.
What is Boyle Temperature?
Answer:
The temperatue at which a real gas exibits ideal behaviour for a considerable range of pressure is called Boyle’s temperature.

Question 36.
What is critical temperature ? Give its value for CO₂.
Answer:
The temperature above which no gas can be liquified how ever high the pressure may be applied is called critical temperature.

• Critical temperature of CO₂ gas is 31.98° C.

Question 37.
What is critical Volume ?
Answer:
The volume occupied by one mole of gas at critical temperature and critical pressure is known as critical volume.

Question 38.
What is critical Pressure ?
Answer:
The pressure required to liquify a gas at critical temperature is known as critical pressure.

Question 39.
What are critical constants ?
Answer:
Critical temperatue (T_C), critical volume (V_C) and critical pressure (P_C) are called as critical constants.

Question 40.
Define vapour Pressure of a liquid.
Answer:
The pressure exerted by the vapour on the liquid surface. When it is in equilibrium with the liquid at a given temperature is known as vapour pressure of the liquid.

Question 41.
What are normal and standard boiling points ? Give their values for H₂O.
Answer:

• The boiling points at 1 atm. pressure are called normal boiling points.
• The boiling points at 1 bar pressure are called standard boiling points.
• For water normal boiling point is 100° C.
• For water standard boiling point is 99.6° C.

Question 42.
Why pressure Cooker is used for cooking food on hills ?
Answer:
At hill areas pressure cooker is used for cooking food because low atmospheric pressure is observed at high altitudes. At high altitudes liquids boil at low temperature. So water boils at low temperature on hills.

Question 43.
What is surface tension ?
Answer:
The force acting at right angles to the surface of the liquid along unit length of surface is called surface tension.

• Units : dynes / cm.

Question 44.
What is laminar flow of a liquid ?
Answer:
In liquids a regular gradation of velocity for layers in passing from one layer to the next observed. This flow of liquid is called Laminar flow.

Question 45.
What is coefficient of Viscosity ? Give its units.
Answer:
The force of friction required to maintain velocity difference of 1 cm. sec^-1 between two parallel layers of a liquid 1 cm. apart and each layer having an area 1cm² is called coefficient of viscosity.

• It is denoted by η
• F = η A \(\frac{\mathrm{du}}{\mathrm{dx}}\)
• Units : Poise : In CGS system 1 poise = 1g. cm^-1 sec^-1.

Short Answer Questions

Question 1.
State and explain Boyle’s law.
Answer:
Boyle’s law : At constant temperature, the volume of a given mass of gas is inversely proportional to pressure of the gas.
If ‘V’ is the volume of a given mass of the gas and its pressure, then the law can be written as
V ∝ \(\frac{1}{P}\) at constant temperature
V = \(\frac{k}{P}\)
∴ PV = k
or P₁V₁ = P₂V₂ = k.
Boyle’s law may also be stated as, “at constant temperature the product of the’ pressure and volume of a given mass of gas is constant.”

Question 2.
State and explain Charle’s law.
Answer:
Charles’ law : At constant pressure, the volume of a given mass of gas is directly proportional to absolute temperature.
V ∝ T at constant pressure
V = kT
\(\frac{V}{T}\) = k
Where V is the volume and T is the absolute temperature. V₁ and V₂ are the initial and final volumes of a given mass of the gas at the absolute temperatures T₁ and T₂ respectively at constant pressure.
\(\frac{V_1}{T_1}\) = k; \(\frac{V_2}{T_2}\) = k
or \(\frac{v_1}{T_1}\) = \(\frac{V_2}{T_2}\) = k

Question 3.
Derive Ideal gas equation. (T.S. Mar. ’16)
Answer:
Ideal gas equation : The combination of the gas laws leads to the development of an equation which relates to the four parameters volume, pressure, absolute temperature and number of moles. This equation is known as ideal gas equation.
In this Boyle’s law and Charles’ law combined together and an equation obtained is called the gas equation.
V ∝ \(\frac{1}{p}\) (Boyle’s law)
V ∝ T (Charles law)
V ∝ n (Avogadro’s law)
Combining above three laws, we can write
V ∝ \(\frac{1}{p}\) ∝ T ∝ n (or) V = R × \(\frac{1}{P}\) × T × n
(Or) PV = nRT
Where V = volume of the gas
P = pressure of the gas
n = no. of moles of gas
T = absolute temperature
R = Universal gas constant.

Question 4.
State and explain Graham’s law of Diffusion. (A.P. Mar.’16) (Mar.’13)
Answer:
Graham’s law of diffusion : At a given temperature and pressure, the rate of diffusion of a gas is inversely proportional to the square root of density, vapour density or molecular weight.

If r₁ and r₂ are the rates of diffusion of two gases d₁ and d₂ are their densities respectively, then
\(\frac{r_1}{r_2}\) = \(\sqrt{\frac{d_2}{d_1}}\)
This eqaution can be written as:

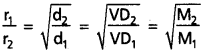
Comparison of the volumes of the gases that diffuse in the same time. Let V₁ and V₂ are the volumes of two gases that diffuse in the same time ‘t’.

When time of flow is same then : \(\frac{\mathrm{r}_1}{\mathrm{r}_2}\) = \(\frac{v_1}{v_2}\)
When volume is the same then : \(\frac{r_1}{r_2}\) = \(\frac{t_2}{t_1}\).

Applications:

• This principle is used in the separation of isotopes like U²³⁵ and U²³⁸.
• Molar mass of unknown gas can be determined by comparing the rate of diffusion of a known gas molecular mass.
• Ansil’s alarms which are used in coal mines to detect the explosive maršh gas works on the principle of diffusion.

Question 5.
State and explain Dalton’s law of Partial pressures.
Answer:
Dalton’s law of Partial pressures : The total pressure exerted by a mixture of chemically non-reacting gases at given temperature and volume, is equal to the sum of the partial pressures of the component gases.
Explanation: Consider a mixture of three gases ¡n a vessel. Let P₁, P₂, P₃ be the partial pressures of the three gases in the mixture. According to Dalton’s law of partial pressures, the pressure (P) of the gaseous mixture is at the same temperature.
P = P₁ + P₂ + P₃

Let n₁, n₂, n₃ be the number of moles of three gases respectively in the mixture. Let ‘V’ be the volume of the mixture of gases at T K temperature.
According to ideal gas equation,

∴ P₁ = x₁ P
In a similar way P₂ = x₂ P and P₃ = x₃P
∴ Partial pressure = mole fraction × total pressure

Question 6.
Deduce
(a) Boyle’s law and
(b) Charle’s law from Kinetic gas equation.
Answer:
a) Deduction of Boyle’s law:
Kinetic gas equation is PV = \(\frac{1}{3} m n u^2\)
PV = \(\frac{1}{3}\) mnu²
= \(\frac{1}{3}\) × \(\frac{2}{2}\) mnu²
= \(\frac{2}{3}\) × \(\frac{1}{2}\) mnu²
PV = \(\frac{2}{3}\) [Kinetic energy (KE)] [∵ KE_{‘n; moles} = \(\frac{1}{2}\) mnu²]
PV = \(\frac{2}{3}\) KT [∵ KE = KT According to kinetic theory]
PV = \(\frac{2}{3}\)KT
According to Boyle’s law T is constant
∴ PV = \(\frac{2}{3}\)(constant)
∴ PV = constant
(or)
P ∝ \(\frac{1}{V}\)
Hence Boyle’s law proved from kinetic gas equation.

b) Deduction of Charle’s law:
Kinetic gas equation is PV = \(\frac{1}{3}\) mnu²
PV = \(\frac{1}{3}\) mnu²
= \(\frac{2}{2}\) × \(\frac{1}{3}\) mnu²
= \(\frac{2}{3}\) × \(\frac{1}{2}\) mnu²
= \(\frac{2}{3}\)(KE) [Kinetic energy (KE) = \(\frac{1}{2}\) mnu²]
PV = \(\frac{2}{3}\)KT [According to kinetic theory KE = KT]
\(\frac{V}{T}\) = \(\frac{2}{3}\) × \(\frac{K}{P}\)
According to Charles law ‘P is constant
∴ \(\frac{V}{T}\) = constant (or) V ∝ T
Hence Charle’s law proved from kinetic gas equation.

Question 7.
Deduce
(a) Graham’s law and
(b) Dalton’s law from Kinetic gas equation.
Answer:
a) Graham’s law: At constant temperature and pressure the rate of diffusion of a gas is inversely proportional to the square root of its density, r ∝ \(\frac{1}{\sqrt{d}}\)
Deduction : Kinetic gas equation is
PV = \(\frac{1}{3}\) mnu² = \(\frac{1}{3}\) mu²
u² = \(\frac{3 P V}{M}\) = \(\frac{3}{d}\)
∴ u = \(\sqrt{\frac{3 \mathrm{P}}{d}}\)
At constant pressure u = k. \(\frac{1}{\sqrt{d}}\)
k = constant; or u ∝ \(\frac{1}{\sqrt{d}}\)
∴ The rate of diffusion of gases depends upon the velocity of the gas molecules.
So r ∝ \(\frac{1}{\sqrt{d}}\).
This is Graham’s law.

b) Dalton’s law of partial pressures : The total pressure exerted by a mixture of chemically non-reacting gases at given temperature and volume, is equal to the sum of the partial pressures of the component gases.
Deduction :
Consider a gas present in vessel of volume = V
no. of molecules = n₁
mass of each molecule = m₁
RMS velocity = u₁
According to kinetic gas equation the pressure of the gas. P₁ = \(\frac{1}{3} \frac{m_1 n_1 u_1^2}{v}\)
When this gas is replaced by another gas in the same vessel, P₂ = \(\frac{1}{3} \frac{m_2 n_2 u_2^2}{V}\)
When these two gases are mixed in the same vessel, the total pressure of the mixture is P = \(\frac{1}{3} \frac{m_1 n_1 u_1^2}{V}+\frac{1}{3} \frac{m_2 n_2 u_2^2}{V}\) = P₁ + P₂
∴ P = P₁ + P₂.
This is Dalton’s law of partial pressures.

Question 8.
Derive an expression for Kinetic Energy of gas molecules.
Answer:
Kinetic gas equation is PV = \(\frac{1}{3}\)mnu²
For one mole of gas ‘n’ the no.of molecules will be equal to Avagadro’s number ‘N’.
∴ m × N = ‘M’ (gram molar mass of the gas)
∴ PV = \(\frac{1}{3}\) Mu²
= \(\frac{2}{2}\) × \(\frac{1}{3}\) Mu²
= \(\frac{2}{3}\) × \(\frac{1}{2}\) Mu²
= \(\frac{2}{3}\) (K.E)
Ideal gas equation for 1 mole of gas is PV = RT
∴ \(\frac{2}{3}\) KE = RT
⇒ KE = \(\frac{3}{2}\) RT
For ‘n’ moles KE = \(\frac{3}{2}\) nRT

Question 9.
Define
(a) RMS
(b) average and
(c) most probable speeds of gas molecules. Give their interrelationship.
Answer:
a) RMS speed:
The square root of mean of the squares of the speeds of all molecules of a gas is known as RMS speed (u_RMS)

b) Average speed:
The arthematic mean of speeds of gas molecules is known as average speed (u_av).

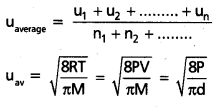
c) Most probable speed:
The speed possessed by the maximum number of molecules of the gas is known as most probable speed (u_mp).
\(u_{m p} \sqrt{\frac{2 R T}{M}}\) = \(\sqrt{\frac{2 P V}{M}}\) = \(\sqrt{\frac{2 P}{d}}\)

Inter relationships : –

• u_mp : u_av : u_rms = \(\sqrt{\frac{2 R T}{M}}\) : \(\sqrt{\frac{8 R T}{\pi M}}\) : \(\sqrt{\frac{3 R T}{M}}\)
  = 1 : 1.128 : 1.224.
• u_av = 0.9213 × u_rms
• u_mp = 0.8166 × u_rms

Question 10.
Explain the physical significance of Vander Waals paramaters.
Answer:
Vander Waals equation : [P + \(\frac{a n^2}{\mathrm{~V}^2}\)] [V – nb] = nRT
Where P = Pressure of the gas
n = Number of moles of the gas
a, b = Vander Waals parameters (or) empirical parameters
V = Volume of the container
R = Gas constant
T = Absolute temperature
Units of ’a’: – bar lit^-2 mole^-2
Units of ’b’: – lit. mol^-1

Significance : –

• ‘a’ is the measure of magnitude of inter molecular forces (attractive) with in the gas and is independent of temperature and pressure. If ‘a’ value is high the gas can be easily liquified.
• ‘b’ is the effective volume of the gas molecule. It indicates the effective size of the gas molecules. If the value of ‘b’ is constant over a long range of temperature and pressure then the gas cannot be compressed easily.

Question 11.
What is Surface Tension of liquids ? Explain the effect of temperature on the surface tension of liquids.
Answer:
Surface tension property (γ): ‘It is defined as the force acting along the surface of a liquid at right angles to any line of 1 unit length.”
It is numerically and dimensionally equal to surface energy. It has dimensions kg. s^-2 and in SI unit Nm^-1.

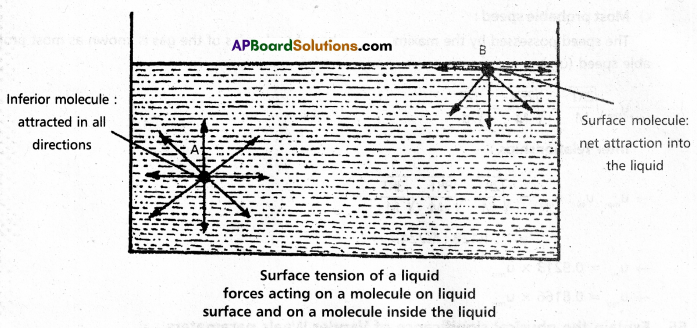
If we consider a molecule in the bulk of the liquid it experiences equal intermolecular forces in all directions. Hence there is no net force acting on it. But a molecule at the surface has intermolecular forces from inside only. Therefore there is a net attractive force on it towards the interior of the liquid. Due to this the surface area of the liquid tends to minimise. That is the molecules experience a downward force and have more energy than the molecules in the bulk.
Surface tension decreases with increase of temperature because of increase in K,E. of molecules and decrease in intermolecular forces,
e.g.:

Question 12.
What is Vapour Pressure of liquids? How the Vapour Pressure of a liquid is related to its boiling point ?
Answer:
The pressure exerted by vapour of a liquid when it is in equilibrium with liquid is known as vapour pressure.
Effect of temperature : When the temperature of a liquid increased the average kinetic energy of molecules increases. This increase in kinetic energy overcomes the attractive forces between the liquid molecules so that liquid molecules rapidly escape into air. Thus rise in temperature raises the escaping tendency of molecules. Hence the vapour pressure of a liquid increases with increase in temperature.

The vapour pressure of a liquid increases with increase of temperature. This goes on until the critical temperature of the liquid is reached. Above the critical temperature liquid state does not exist when the vapour pressure of the liquid becomes equal to the external (atmospheric) pressure the liquid is said to be boiling and the temperature at which this happens is known as boiling point.

For water the boiling point is 100°C at 1. atm pressure. If the external pressure is reduced, the liquid boils at lower temperature. The boiling point of a liquid can be increased by increasing the external pressure.

Question 13.
Define Viscosity and Coefficient of Viscosity. How does the Viscosity of liquids varies with temperature.
Answer:
Viscosity : Viscosity is a measure of resistance to flow of liquids. This arises due to internal friction between layers of fluids as they slip past one another while liquid flows.

Coefficient of Viscosity:

The force of friction required to maintain velocity difference of 1 cm. sec^-1 between two parallel layers of a liquid 1 cm. apart and each layer having an area 1 cm² is called coefficient of viscosity.

• It is denoted by η
• F = ηA\(\frac{d u}{d x}\)
• Units : Poise : In CGS system 1 poise = 1g. cm^-1 sec^-1.
• Viscosity of liquids decrease with increase of temperature due to high kinetic energy of molecules that over come the inter molecular forces.

Long Answer Questions

Question 1.
Write notes on Intermolecular Forces.
Answer:
Intermolecular forces :
a) Ion – Dipole forces : Ion dipole forces are mainly important in aqueous solutions of ionic substances such as NaCl in which dipolar water molecules surround the ions.

Water molecules are polar and in them hydrogen atoms possess partial positive charges and oxygen atoms possess partial negative charges due to electronegativity difference between hydrogen and oxygen atoms. When ionic compounds like NaCl dissolve in water, they dissociate into component ions like Na⁺ and Cl^–. Now the water molecules orient in the presence of ions in such a way that the positive end of the dipole is near an anion and the negative end of the dipole is near a cation.

b) Dipole-Dipole forces : Neutral but polar molecules experience dipole-dipole forces. These are due to the electrical interactions among dipoles on neighbouring molecules. These forces are again attractive between unlike poles and repulsive between like poles and depend on the orientation of the molecules. The net force in a large collection of molecules results from many individual interactions of both types. The forces are generally weak and are significant only when the molecules are in close contact.

c) London dispersion forces : These forces result from the motion of electrons around atoms. Take, for example, atoms of helium. The electron distribution around a helium atom is for averaged over time spherically symmetrical. However, at a given instant the electron distribution in an atom may be unsymmetrical giving the atom a short – lived dipole moment. This instantaneous dipole on one atom can affect the electron distribution is neighbouring atoms and induce temporary dipoles in those neighbours. As a result, weak attractive forces develop known as London forces or dispersion forces. London forces are generally small. Their energies are in the range 1 – 10k J mol^-1.

d) Dipole – Induced Dipole forces : These forces are between polar molecules with permanent dipole moments and the molecules with no permanent dipole moment. Permanent dipole of the polar molecule induces dipole on the electrically neutral molecule by deforming into electronic cloud.
Magnitude of these forces depends on the magnitude of the dipole moment of permanent dipole and polarisatricity of neutral molecule. This interaction is proportional to \(\left(\frac{1}{r^2}\right)\), where r = distance between molecules.

Question 2.
State Boyle’s law, Charle’s law and Avogadro’s law and derive Ideal gas equation.
Answer:
Boyle’s law : At constant temperature, the volume of a given mass of gas is inversely proportional to pressure of the gas.
If ‘V is the volume of a given mass of the gas and ‘P’ its pressure, then the law can be written as V ∝ \(\frac{1}{P}\) at constant temperature
V = \(\frac{k}{P}\)
∴ PV = k or P₁V₁ = P₂V₂ = k

Boyle’s law may also be stated as, “at constant temperature the product of the pressure and volume of a given mass of gas is constant.”

Charles’ law: At constant pressure, the volume of a given mass of gas is directly proportional to absolute temperature.
V ∝ T at constant pressure
V = kT
\(\frac{\mathrm{T}}{\mathrm{T}}\) = k

Where V is the volume and T is the absolute temperature. V₁ and V₂ are the initial and final volumes of a given mass of the gas at the absolute temperatures T₁ and T₂ respectively at constant pressure.
\(\frac{V_1}{T_1}\) = k ; \(\frac{V_2}{T_2}\) = k
or \(\frac{V_1}{T_1}\) = \(\frac{V_2}{T_2}\) = k
Avogadro’s law : Equal volumes of all gases contain equal number of moles at constant temperature and pressure.
V ∝ n (pressure and temperature are constant).

Ideal gas equation : The combination of the above gas laws leads to the development of an equation which relates to the four parameters volume, pressure, absolute temperature and number of moles. This equation is known as ideal gas equation.

In this Boyle’s law and Charles’ law combined together and an equation obtained called the gas equation.
V ∝ \(\frac{1}{P}\) (Boyle’s law) ‘
V ∝ T (Charles law)
V ∝ n (Avogadro’s law)

Combining above three laws, we can write
V ∝ \(\frac{1}{P}\) ∝ T ∝ n (or) V = R × \(\frac{1}{P}\) × T × n
(Or) PV = nRT
Where V = volume of the gas
P = pressure of the gas
n = no. of moles of gas
T = absolute temperature
R = Universal gas constant

Question 3.
Write notes on diffusion of Gases.
Answer:
Diffusion : The property of gases to spread and occupy the available space is known as diffusion.

• It is a non – directional phenomenon.
  Effusion : The escape of a gas from high pressure region into space through a fine hole is called effusion.
• It is uni directional phenomenon.

Rate of diffusion : No. of molecules diffused per unit time is called rate of diffusion.

Graham’s law of diffusion : At a given temperature and pressure, the rate of diffusion of a gas is inversely proportional to the square root of density, vapour density or molecular weight.
r ∝ \(\frac{1}{\sqrt{d}}\) ; r ∝ \(\frac{1}{\sqrt{V D}}\) ; r ∝ \(\frac{1}{\sqrt{M}}\)
If r₁ and r₂ are the rates of diffusion of two gases d₁ and d₂ are their densities respectively, then
\(\frac{r_1}{r_2}\) = \(\sqrt{\frac{\mathrm{d}_2}{\mathrm{~d}_1}}\)
This equation can be written as :

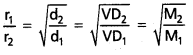
Comparison of the volumes of the gases that diffuse in the same time. Let V₁, and V₂ are the volumes of two gases that diffuse in the same time t’.

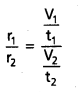
When time of flow is same then \(\frac{r_1}{r_2}\) = \(\frac{V_1}{V_2}\)
When volume is the same then : \(\frac{r_1}{r_2}\) = \(\frac{t_2}{t_1}\)

Applications :

• This principle is used in the separation of isotopes like U²³⁵ and U²³⁸.
• Molar mass of unknown gas can be determined by comparing the rate of diffusion of a known gas molecular mass.
• Ansil’s alarms which are used in coal mines to detect the explosive marsh gas works on the principle of diffusion.

Question 4.
State and explain Dalton’s law of Partial Pressures.
Answer:
Dalton’s law of Partial pressures : The total pressure exerted by a mixture of chemically non-reacting gases at given temperature and volume, is equal to the sum of the partial pressures of the component gases.

Explanation: Consider a mixture of three gases in a vessel. Let P₁, P₂, P₃ be the partial pressures of the three gases in the mixture. According to Dalton’s law of partial pressures, the pressure (P) of the gaseous mixture is at the same temperature.
P = P₁ + P₂ + P₃
Let n₁, n₂, n₃ be the number of moles of three gases respectively in the mixture. Let V be the volume of the mixture of gases at T K temperature.
According to ideal gas equation,
P₁ = \(\frac{n_1 R T}{V}\) ; P₂ = \(\frac{\mathrm{n}_2 \mathrm{RT}}{\mathrm{V}}\) ; P₃ = \(\frac{\mathrm{n}_3 \mathrm{RT}}{\mathrm{V}}\)
∴ Total pressure of the mixture P = P₁ + P₂ + P₃
P = \(\frac{n_1 R T}{V}\) + \(\frac{n_2 R T}{V}\) + \(\frac{n_3 R T}{V}\)
P = \(\frac{R T}{V}\)(n₁ + n₂ + n₃)
Since nn₁ + n2n₂ + nn₃ = n

∴ P₁ = x₁ P
In a similar way P₂ = x₂ P and P₃ = x₃P
∴ Partial pressure = mole fraction × total pressure

Question 5.
Write the postulates of Kinetic Molecular Theory of Gases.
Answer:
Assumptions:

1. Gases are composed of minute particles called molecules. All the molecules of a gas are identical.
2. Gaseous molecules are always, at a random movement. The molecules are moving in all possible directions in straight lines with very high velocities. They keep on colliding against each other and against the walls of the vessel at very small intervals of time.
3. The actual volume occupied by the molecules is negligible when compared to the total volume occupied by the gas.
4. There is no appreciable attraction or repulsion between the molecules.
5. There is no loss of kinetic energy when the molecules collide with each other or with the wall of vessel. This is because the molecules are spherical and perfectly elastic in nature.
6. The pressure exerted by the gas is due to the bombardment of the molecules of the gas on the walls of the vessel.
7. The average kinetic energy of the molecules of the gas is directly proportional to the absolute temperature, Average K.E. ∝ T.
8. The force of gravity has no effect on the speed of gas molecules.

Boyle’s law : According to kinetic theory of gases, the pressure of a gas is due to collisions of gas molecules on the walls of the vessel. At a particular temperature the molecules make definite number of collisions with the walls of the vessel; When the volume of the vessel is reduced the molecules have to travel lesser distance only before making collisions on the walls. As a result the number of collisions per unit increases. The pressure then increases, i.e., the pressure increases when the volume is reduced at constant temperature. This explains Boyle’s law.

Charles’ law : According to kinetic theory of gases, the average kinetic energy of the molecules is directly proportional to the absolute temperature of the gas.
K.E. ∝ T
but K.E. = \(\frac{1}{2}\) mc²

As temperature increases, the velocity of the molecules also increases. As a result the molecules make more number of collisions against the walls of the vessel. This results in an increase of pressure if the volume is kept constant. If the volume is allowed to increase the number of collisions decrease due to the increased distance between the molecules and the walls of the vessel. The pressure then decreases. In other words, with rise of temperature, the volume should increase in order to keep the pressure constant.
V ∝ T at constant pressure.
This is Charles’ law.

Question 6.
Deduce gas laws from Kinetic gas equation.
Answer:
a) Deduction of Boyle’s law :
Kinetic gas equation is PV = \(\frac{1}{3}\) mnu²
PV = \(\frac{1}{3}\) mnu²
= \(\frac{1}{3}\) × \(\frac{2}{2}\) mnu²
= \(\frac{2}{3}\) × \(\frac{1}{2}\) mnu²
PV = \(\frac{2}{3}\)[Kinetic energy (KE)] [∵ KE_{‘n’ moles} = \(\frac{1}{2}\) mnu²]
PV = \(\frac{2}{3}\)KT [∵ KE = KT According to kinetic theory]
PV = \(\frac{2}{3}\)KT
According to Boyle’s law T is constant
∴ PV = \(\frac{2}{3}\)(constant)
∴ PV = constant
(or)
P ∝ \(\frac{1}{V}\)
Hence Boyle’s law proved from kinetic gas equation.

b) Deduction of Chartes law:
Kinetic gas equation is PV = \(\frac{1}{3}\) mnu²
PV = \(\frac{1}{3}\) mnu²
= \(\frac{2}{2}\) × \(\frac{1}{3}\) mnu²
= \(\frac{2}{3}\) × \(\frac{1}{2}\) mnu²
= \(\frac{2}{3}\) (KE) [Kinetic Energy (KE) = \(\frac{1}{2}\) mnu²]
PV = \(\frac{2}{3}\)KT [According to kinetic theory KE = KT]
\(\frac{V}{T}\) = \(\frac{2}{3}\) × \(\frac{K}{P}\)
According to Charles law P’ is constant
∴ \(\frac{V}{T}\) = constant (or) V ∝ T
Hence Charles law proved from kinetic gas equation.

c) Graham’s law: At constant temperature and pressure the rate of diffusion of a gas is inversely proportional to the square root of its density, r ∝ \(\frac{1}{\sqrt{d}}\)
Deduction: Kinetic gas equation is
Pv = \(\frac{1}{3}\) mnu² = \(\frac{1}{3}\) Mu²

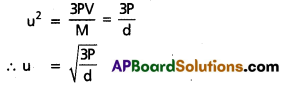
At constant pressure u = k. \(\frac{1}{\sqrt{d}}\)
k = constant; or u ∝ \(\frac{1}{\sqrt{d}}\)
∵ The rate of diffusion of gases depends upon the velocity of the gas molecules.
So r ∝ \(\frac{1}{\sqrt{d}}\)
This is Graham’s law.

d) Dalton’s law of partial pressures : The total pressure exerted by a mixture of chemically non-reacting gases at given temperature and volume, is equal to the sum of the partial pressures of the component gases.

Deduction:
Consider a gas present in vessel of volume = V
no. of molecules = n₁
mass of each molecule = m₁
RMS velocity = u₁

According to kinetic gas equation the pressure of the gas. P₁ = \(\frac{1}{3} \frac{m_1 n_1 u_1^2}{V}\)
When this gas is replaced by another gas in the same vessel, p₂ = \(\frac{1}{3} \frac{m_2 n_2 \cdot u_2^2}{V}\)
When these two gases are mixed in the same vessel, the total pressure of the mixture is P = \(\frac{1}{3} \frac{m_1 n_1 u_1^2}{v}\) + \(\frac{1}{3} \frac{m_2 n_2 u_2^2}{V}\) = P₁ + P₂
∴ P = P₁ + P₂
This is Dalton’s law of partial pressures.

Question 7.
Explain Maxwell-Boltzmann distribution curves of molecular speeds and give the important conclusions. Discuss the effect of temperature on the distribution of molecular speeds.
Answer:
According to kinetic gas equation it was assumed that all the molecules in a gas have the same velocity. But it is not correct. When any two molecules collide exchange of energy takes place and hence their velocities keep on changing. At any instant few molecules may have zero velocity, a few molecules may be at high velocities and some may be with low velocities.

The distribution of speeds between different molecules were worked out by Maxwell by applying probability considerations.

If one plots a graph between fraction of molecules \(\frac{\Delta \mathrm{N}}{\mathrm{N}}\) vs velocity one gets distribution curve of the type.

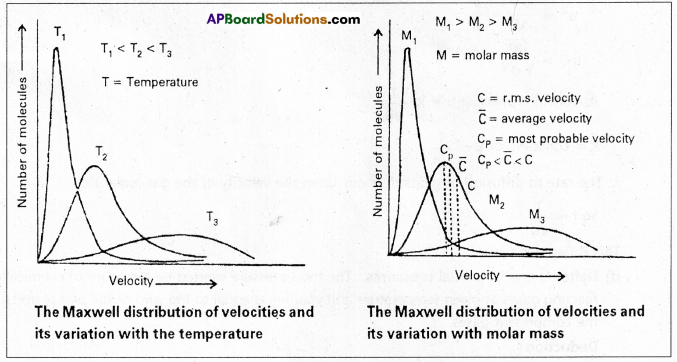
These curves are shown at different temperatures T₁ T₂ (T₁ < T₂)

The graph reveals that

1. There are no molecules with zero velocity and only very few molecules possess the highest velocity.
2. The velocities of most of the molecules lie near a mean value.
3. As the temperature of the gas is increased, the curve becomes more flattened and shifts towards higher velocity. It means that at higher temperature the number of molecules possessing higher velocities is more than at lower temperature.

The peak point corresponds to the most probable velocity. It is the velocity possessed by maximum number of molecules.
The average velocity of the molecules is slightly higher than the most probable velocity. The RMS velocity is slightly higher than the average velocity.

Question 8.
Write notes on the behaviour of real gases and their deviation from ideal behavior.
Answer:
Real gases are also called non – ideal gases; A gas which does not obey ideal gas equation PV = nRT is called Real gas.

• Real gases show ideal behaviour at low pressure and high temperature.
  The deviation of real gas from ideal behaviour can be measured in terms compressibility factor (Z), which is the ratio of product PV and nRT. (i.e.,) Z = \(\frac{\mathrm{PV}}{\mathrm{nRT}}\)

For ideal gas, Z = 1 at all temperatures and pressures because PV = nRT. The graph of Z Vs P will be a straight line parallel to pressure axis. For gases which deviate from ideality, value of Z deviates from unity. At very low pressures all gases shown Z = 1 and behave as ideal gas. At low pressures, inter molecular forces are negligible hence show ideal behaviour. At high pressures all the gases have Z > 1. These are more difficult to compress. At intermediate pressures, most gases have Z < 1.

Question 9.
Derive the Vander Waals equation of state. Explain the importance of Vander Waal’s gas eqaution.
Answer:
Vander Waal’s equation of state : Vander Waal’s proposed an approximate equation of state which involves the intermolecular interactions that contribute to the deviations of a gas from perfect gas law. It may be explained as follows. The repulsive interactions between two molecules cannot allow them to come closer than a certain distance. Therefore, for the gas molecules the available volume for free travel is not the volume of the container V but reduced to an extent proportional to the number of molecules present and the volume of each exclude.

Therefore, in the perfect gas equation a volume correction is made by changing v to (v – nb). Here, ‘b’ is the proportionality constant between the reduction in volume and the amount of molecules present in the container. P = \(\frac{n R T}{V-n b}\) If pressure is low, the volume is large compared with the volume excluded by the molecules (V > > nb). The nb can be neglected in the denominator and the equation reduces to the perfect gas equation of state.

The effect of attractive interactions between molecules is to reduce the pressure that the gas exerts. The attraction experienced by a given molecule is proportional to the concentration n/V of molecules in that container. As the attractions slow down the molecules, the molecules strike the waals less frequently and strike with a weaker impact. Therefore, we can expect the reduction in pressure to be proportional to the square of the molar-concentration, one factor of n/V showing the reduction in frequency of collisions and the other factor the reduction in the strength of their impulse.

Reduction in pressure ∝ \(\left(\frac{n}{V}\right)^2\)
Reduction in pressure = a. \(\left(\frac{n}{v}\right)^2\),
Where a = the proportionality constant.
Vander Waals equation is

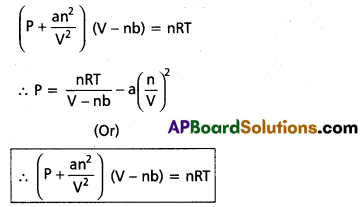
The equation is called Vander Waals equation of state.

The constants ‘a’ and ‘b’ known as Vander Waals parameters (or) empirical parameters. They depend on the nature of the gas independent of temperature.

Significance : –

• ‘a’ is the measure of magnitude of inter molecular forces (attractive) with in the gas and is independent of temperature and pressure. If ‘a’ value is high the gas can be easily liquified.
• ‘b’ is the effective volume of the gas molecule. It indicates the effective size of the gas molecules. If the value of ‘b’ is constant over a long range of temperature and pressure then the gas cannot be compressed easily.

Question 10.
Explain the principle underlying the liquefacation of gases.
Answer:
Liquifacation of gases can be done by decreasing the temperature and increasing the pressure.

Liquefaction of gases: Any gas, if it to be liquefied, it must be cooled below its critical temperature. A gas liquefies if it is cooled below its boiling point at given pressure. For example, chlorine at room pressure say 1 atmosphere can be liquefied by cooling it to – 34.0°C in a dry ice bath. For N₂ and O₂ that have very low boiling points -196°C and -183°C. Such simple technique is not possible. Then, to liquify such type of gases the technique based on intermolecular forces is used. It is as follows. If the velocities of molecules are reduced to such lower values that neighbours can attract each other by their interaction or intermolecular attractions, then the cooled gas will condense to a liquid.

For this, the molecules are allowed to expand into available volume without supplying any heat from outside. In this, the molecules have to overcome the attractions of their neighbours and in doing so, the molecules convert some of their kinetic energy into potential energy and now travel slowly. The average velocity decreases and therefore the temperature of the gas decreases and the gas cools down compared to its temperature before its expansion. For this the gas is allowed to expand through a narrow opening called throttle. This way of cooling of gas by expansion from high pressure side to low pressure is called Joule – Thomson effect.

Question 11.
Write notes on the following properties of liquids
(a) Vapour Pressure
(b) Surface Tension
(c) Viscosity.
Answer:
(a) Vapour Pressure : The pressure exerted by vapour of a liquid when it is in equilibrium with liquid is known as vapour pressure.
Effect of temperature : When the temperature of a liquid increased the average kinetic energy of molecules increases. This increase in kinetic energy overcomes the attractive forces between the liquid molecules so that liquid molecules rapidly escape into air. Thus rise in temperature raises the escaping tendency of molecules. Hence the vapour pressure of a liquid increases with increase in temperature.

The vapour pressure of a liquid increases with increase of temperature. This goes on until the critical temperature of the liquid is reached. Above the critical temperature liquid state does not exist when the vapour pressure of the liquid becomes equal to the external (atmospheric) pressure the liquid is said to be boiling and the temperature at which this happens is known as boiling point.

For water the boiling point is 100°C at 1. aim pressure. If the external pressure is reduced, the liquid boils at lower temperature. The boiling point of a liquid can be increased by increasing the external pressure.

b) Surface tension property (γ) : “It is defined as the force acting along the surface of a liquid at right angles to any line of 1 unit length.”
It is numerically and dimensionally equal to surface energy. It has dimensions kg. s^-2 and in SI unit Nm^-1

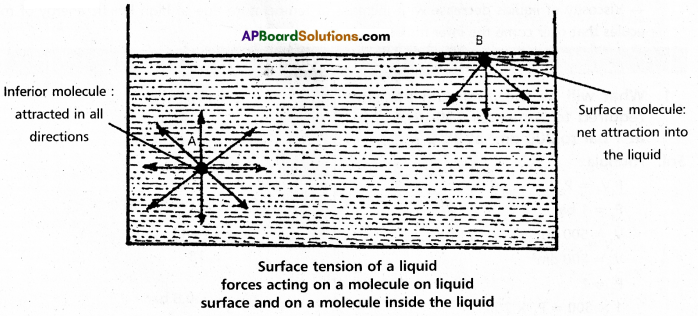
If we consider a molecule in the bulk of the liquid it experiences equal intermolecular forces in all directions. Hence there is no net force acting on it. But a molecule at the surface has intermolecular forces from inside only. Therefore there is a net attractive force on it towards the interior of the liquid. Due to this the surface area of the liquid tends to minimise. That is the molecules experience a downward force and have more energy than the molecules in the bulk.

Surface tension decreases with increase of temperature because of increase in K, E. of molecules and decrease in intermolecular forces.
e.g.:

c) Viscosity : Viscosity is a measure of resistance to flow of liquids. This arises due to internal friction between layers of fluids as they slip past one another while liquid flows.
Coefficient of Viscosity:
The force of friction required to maintain velocity difference of 1cm. sec^-1 between two parallel layers of a liquid 1 cm. apart and each layer having an area 1cm² is called coefficient of viscosity.

• It is denoted by η
• F = η A \(\frac{\mathrm{du}}{\mathrm{dx}}\)
• Units : Poise : In CGS system 1 poise = 1g. cm^-1 sec^-1.
• Viscosity of liquids decrease with increase of temperature due to high kinetic energy of molecules that over come the inter molecular forces.

Solved Problems

Question 1.
What will be the minimum pressure required to compress 500 dm³ of air at 1 bar to 200 dm³ at 30°C?
Solution:
Formula:
P₁y₁ = P₂y₂
P₁ = 1 bar
V₁ = 500 dm³
V₂ = 200 dm³
P₂ = ?
1 × 500 = P₂ × 200
P₂ = \(\frac{5}{2}\) = 2.5 bar.

Question 2.
A vessel of 120 mL capacity contains a certain amount of gas at 35°C and 1.2 bar pressure. The gas is transferred to another vessel of volume 180 mL at 35 °C. What would be its pressure ?
Solution:
Formula:
P₁V₁ = P₂V₂
P₁ = 1.2 bar
V₁ = 120 ml
V₂ = 180 ml
P₂ = ?
1.2 × 120 = P₂ × 180
P₂ = \(\frac{1.2 \times 12}{18}\)
= \(\frac{2.4}{3}\) = 0.8 bar

Question 3.
Using the equation of state pV = nRT; show that at a given temperature density of a gas is proportional to gas pressure p.
Solution:
Consider the equation of state .
PV = nRT
PV = \(\frac{w}{M} R T\)
P = \(\frac{W}{V} \times \frac{R T}{M}\)
P = \(\frac{\mathrm{dRT}}{\mathrm{M}}\) (∵ d = \(\frac{w}{V}\))
From the above relation
P ∝ d

Question 4.
At 0°C, the density of a certain oxide of a gas at 2 bar is same as that of dinitrogen at 5 bar. What is the molecular mass of the oxide?
Solution:

• Given two gases one is unknown oxide and another one is dinitrogen.
• Density of two gases is same
  

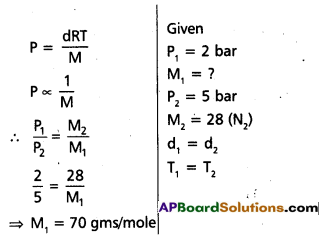
Question 5.
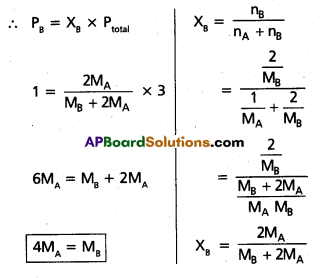
Pressure of 1 gm. of an ideal gas A at 27 °C is found to be 2 bar. When 2 g of another ideal gas B is introduced in the same flask at same temperature the pressure becomes 3 bar. Find a relationship between their molecular masses.
Solution:
Given
Weight of gas A = 1 gm
Weight of gas B = 2 gms
Molecular mass of A = M_A
Molecular mass of B = M_B
Pressure of A = P_A = 2 bar
Given Total pressure = 3 bar (P_A + P_B)
∴ P_B = 3 – 2 = 1 bar

Question 6.
The drain cleaner, Drainex contains small bits of aluminum which react with caustic soda to produce dihydrogen. What volume of dihydrogen at 20°C and one bar will be released when 0.15 g of aluminium reacts?
Solution:
Chemical equation is
2Al + 2 NaOH + 2H₂O → 2 NaAlO₂ + 3H₂
From the above equation
2 gram atom of Al liberates 3 moles of H₂ at NTP
2 × 27 gms Al liberates 3 × 22.4 lit.
0.15 gms of Al liberates?
= \(\frac{0.15 \times 3 \times 22.4}{2 \times 27}\)
= 0.1866 li.t = 186.6 ml
P₁ = 1.013 bar P₂ = 1 bar
V₁ = 186.6 ml V₂ = ?
T₁ = 273 K T₂ = 20° C = 293 K
Formulae:

Question 7.
What will be the pressure extracted by a mixture of 3.2 g of methane and 4.4 g of carbon dioxide contained in a 9 dm³ flask at 27 °c?
Solution:
Formula:
Given 3.2 gmš of CH₄
no.of moles of CH₄ = \(\frac{w t}{\text { GMW }}\) = \(\frac{3.2}{16}\) = 0.2
no.of moles of CO₂ = \(\frac{4.4}{44}\) = 0.1
∴ n = \(\mathrm{n}_{\mathrm{CH}_4}\) + \(\mathrm{n}_{\mathrm{CO}_2}\)
= 0.2 + 0.1 = 0.3
R = 8.314
T = 27°C = 300 K
V = 9 dm³
PV = nRT
P = \(\frac{n R T}{V}\)
= \(\frac{0.3 \times 8.314 \times 300}{9}\) = 83.14
= 83.14 × 10³ pa
= 83.14 × 10⁴ pa
∴ P = 8.314 × 10⁴ pa

Question 8.
What will be the pressure of the gaseous mixture when 0.5 L of H₂ at 0.8 bar and 2.0 L of dioxygen at 0.7 bar are introduced in a 1 L vessel at 27°C?
Solution:
Case – I
Hydrogen gas
P₁ = 0.8 bar
P₂ = ?
V₁ = 0.5 lit
V₂ = 1.0 lit
P₁y₁ = P₂V₂
P₂ = \(\frac{0.8 \times 0.5}{1}\)
P₂ = 0.4 bar
Partial pressure of H₂ = 0.4 bar. \(\left[\mathrm{P}_{\mathrm{H}_2}\right]\)

Case-II:
Oxygen gas
P₁ = 0.7 bar
V₁ = 2 lit
V₂ = 1.0 lit
P₂ = ?
P₁V₁ = P₂V₂
P₂ = \(\frac{P_1 V_1}{V_2}=\frac{0.7 \times 2}{1}\)
= 1.4 bar
Partial pressure of O₂ = 1.4 bar. \(\left[\mathrm{P}_{\mathrm{O}_2}\right]\)
∴ Total pressure = \(P_{\mathrm{H}_2}\) + \(P_{\mathrm{O}_2}\)
= 0.4 + 1.4 = 1.8 bar

Question 9.
Density of a gas is found to be 5.46 g/dm³ at 27 °c at 2 bar pressure. What will be its density at STP?
Solution:
d₁ = 5.46 gm/dm³
T₁ = 27° C = 300 K
P₁ = 2 bar
P₂ = 1.013 bar (STP)
T₂ = 273 K(STP)
d₂ = ?

Question 10.
34.05 mL of phosphorus vapour weighs 0.0625 g at 546 °c and 0.1 bar pressure. What is the molar mass of phosphorus ?
Solution:
P = 0.1 bar
W = 0.0625 gms
R = 0.083 bar dm³ k^-1 mol^-1
V = 34.05 × 10^-3 lit
T = 546°C = 819 K
Formula:
PV = nRT
PV = \(\frac{w}{M} R T\)
0.1 × 34.05 × 10^-3 = \(\frac{0.0625}{M}\) × 0.083 × 819
M = \(\frac{0.0625 \times 0.083 \times 819}{0.1 \times 34.05 \times 10^{-3}}\)
= \(\frac{0.0625 \times 83 \times 819}{34.05}\)
= 124.77 gm/mole.

Question 11.
A student forgot to add the reaction mixture to the round bottomed flask at 27 °C but instead he/she placed the flask on the flame. After a lapse of time, he realized his mistake and using a pyrometer he found the temperature of the flask was 477 °C. What fraction of air would have been expelled out ?
Solution:
Formula:
T₁ = 27° C – 300 K
T₂ = 477° C = 750 K
\(\frac{V_1}{T_1}\) = \(\frac{V_2}{T_2}\)
\(\frac{V_1}{300}\) = \(\frac{V_2}{750}\)
V₂ = \(\frac{750 \times \mathrm{V}_1}{300}\)
V₂ = 2.5 V₁
The volume of air expelled = V₂ – V₁
= 2.5V₁ – V₁
= 1.5V₁
Fraction of air expelled out
= \(\frac{1.5 \mathrm{~V}_1}{2.5 \mathrm{~V}_1}\) = \(\frac{1.5}{2.5}\) = \(\frac{15}{25}\) = \(\frac{3}{5}\)

Question 12.
Calculate the temperature of 4.0 mol of a gas occupying 5 dm³ at 3.32 bar.
(R = 0.083 bar dm³ k^-1 mol^-1)
Solution:
Formulae: —
P = 3.32 bar
V = 5 dm³
R = 0.083 bar dm³ k^-1 mol^-1
n = 4 moles
PV = nRT
T = \(\frac{\mathrm{PV}}{\mathrm{nR}}\)
= \(\frac{3.32 \times 5}{4 \times 0.083}\)
= \(\frac{16.6}{0.332}\)
= 50
∴ T = 50 k

Question 13.
Calculate the total number of electrons present in 1.4 g of dinitrogen gas.
Solution:
14 gms of N₂ gas contains
6.023 × 10²³ atoms
1.4 gms of N₂ gas contains
6.023 × 10²² atoms
Each ‘N’ atom contains 7 electrons.
∴ Number of electrons present in 1.4 gms of Nitrogen
= 6.023 × 10²² × 7
= 42.161 × 10²²
= 4.2161 × 10²³ electrons.

Question 14.
How much time would it take to distribute one Avogadro number of wheat grains, if 10¹⁰ grains are distributed each second ?
Solution:
Given that
10¹⁰ grains are distributed in each second i.e., one second Avagodro number means 6.023 × 10²³
6.023 × 10²³ grains distributed in ?
X seconds
x = \(\frac{6.023 \times 10^{23}}{10^{10}}\) = 6.023 × 10¹³ seconds
The time taken to distribute the one Avagadro number of grains
= \(\frac{6.023 \times 10^{13}}{60 \times 60 \times 24 \times 365}\)
= \(\frac{6.023 \times 10^{13}}{3.153 \times 10^7}\) = 1.909 × 10⁶ years.

Question 15.
Ammonia gas diffuses through a fine hole at the rate 0.5 lit min^-1. Under thé same conditions find the rate of diffusion of chlorine gas.
Solution:
Rate of diffusion of ammonia (r₁)
= 0.5 lit min^-1
Molecular weight of ammonia (M₁) = 17
Rate of diffusion of chlorine (r₂) = ?
Molecular weight of chlorine (M₂) = 71
According to Graham’s law of diffusion

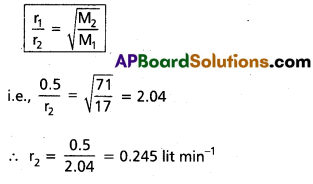
∴ Rate of diffusion of Cl₂ = 0.245 lit/min.

Question 16.
Find the relative rates of diffusion of CO₂ and Cl₂ gases.
Solution:

Question 17.
If 150 mL carbon monoxide effused in 25 seconds, what volume of methane would diffuse in same time?
Solution:
Rate of diffusion of CO (r₁)

Molecular weight of CO (M₁) = 28
Rate of diffusion of methane (r₂)

Molecular weight of methane (M₂) = 16
According to Graham’s law of diffusion

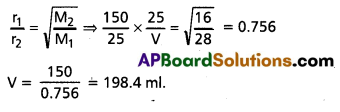
Question 18.
Hydrogen chloride gas is sent into a 1oo metre tube from one end ‘A’ and ammonia gas from the other end ‘B’, under similar conditions. At what distance from ‘A’ will be the two gases meet?
Solution:

The two gases HCl and NH₃ diffuse into the pipe from the ends A and B respectively to meet at a point O as indicated by formation of white ring of NH₄Cl. If the distance AO is x meters, the distance OB will be (100 – x) metres.
According to Graham’s law of diffusion. Ration of rates of diffusion of HCl and NH₃ gas is given by
\(\frac{735 \mathrm{~mm} \times 101.3 \mathrm{kPa}}{1760 \mathrm{~mm}}\) = 98 k Pa
It means that the two gases meet at the point O such that the ratio of the distances from the end A to O and B to O is 0.68 : 1.00
∴ \(\frac{0.68}{1}\) = \(\frac{x}{(100-x)}\)
or 0.68 (100 – x) = x or 68 – 0.68 x = x
or 68 = x + 0.68 x or 68 = x (1 + 0.68)
= 1.68 x
x = \(\frac{68}{1.68}\) = 40.48 metres.
Hence, the two gases meet at a distance of 40.48 metres from the end ‘A’.

Question 19.
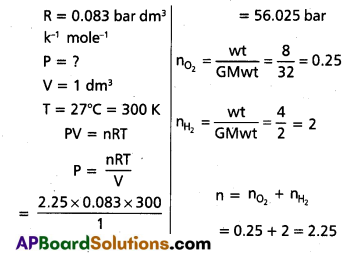
Calculate the total pressure in a mixture of 8 g of dioxygen and 4 g of dihydrogen confined in a vessel of 1 dm³ at 27°C. R = 0.083 bar dm³ K^-1 mol^-1.
Solution:
Formula:

Question 20.
Calculate the total pressure in a mixture of 3.5g of dinitrogen 3.0g of dihydrogen and 8.0g dioxygen confined in vessel of 5 dm³ at 27°C (R = 0. 083 bar dm³ k^-1 mol^-1)
Solution:
Formula:
V = 5 dm³

Question 21.
Pay load is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the pay load when a balloon of radius 10m, mass 100 kg is filled with helium at 1.66 bar at 27°C. (Density of air = 1.2 kg m^-3 and R = 0.083 bar dm³ k^-1 mol^-1).
Solution:
Formula :
r = 10 m
m = 100 kg
T = 27° C = 300 K
d = 1.22 kg/m³
Volume of the ballon = \(\frac{4}{3} \pi r^3\)
= \(\frac{4}{3} \times \frac{22}{7} \times 10^3\)
= 4190.5 m³
P = 1.66 bar
T = 300 K
V = 4190.5 m³
R = 0.083 bar dm³ k^-1 mol^-1
PV = nRT
n = \(\frac{\mathrm{PV}}{\mathrm{RT}}\) = \(\frac{1.66 \times 4190.5}{0.083 \times 10^{-3} \times 300}\)
= 2793.70 moles
= 0.083 × 10^-3 bar m³k^-1mol^-1
∴ Weight of 279370 moles of He
= 279390 × \(\frac{4}{1000}\)
= 1117.48 kg
Total weight of balloon = 100 + 1117.48
= 1217.48 kg
Maximum weight of He = V × d
=4190.5 × 1.2
= 5028.6 kg
∴ Payload = 5028.6 – 1219.48
= 3811.12 kg.

Question 22.
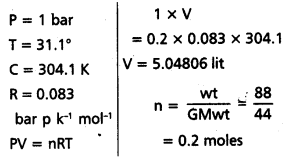
Calculate the volume occupied by 8.8 g of CO₂ at 31 .1°C and 1 bar pressure. R = 0.083 bar L K^-1 mol^-1.
Solution:
Formula:

Question 23.
2.9 g of a gas at 95 °C occupied the same volume as 0.184 g of dihydrogen at 17°C, at the same pressure. What is the molar mass of the gas?
Solution:
Given unknown gas and dihydrogen
For unknown gas
V₁ = V
n₁ = \(\frac{2.9}{\mathrm{~m}}\)
T₁ = 95° C = 368 K
P₁V₁ = n₁RT₁
P₁ = \(\frac{n_1 R T_1}{V_1}\)
= \(\frac{2.9}{m} \times \frac{R \times 368}{V}\)
For dihydrogen

Question 24.
A mixture of dihydrogen and dioxygen at one bar pressure contains 20% by weight of dihydrogen. Calculate the partial pressure of dihydrogen.
Solution:
Given 20% by wt of dihydrogen so 80% oxygen remained for dihydrogen
n = \(\frac{w t}{\text { GMwt }}\) = \(\frac{0.2}{2}\) = 0.1
For dioxygen
n = \(\frac{w t}{\text { GMwt }}\) = \(\frac{0.8}{32}\) = 0.025
mole fraction of H₂
= \(\frac{0.1}{0.1+0.025}\) = \(\frac{0.1}{0.125}\) = 0.8
Partial pressure of dihydrogen
= mole fraction of H₂ × P_total
= 0.8 × 1 = 0.8 bar

Question 25.
What would be the SI unit for the quantity \(\frac{\mathrm{PV}^2 \mathrm{~T}^2}{\mathrm{n}}\)?
Solution:
Given quantity \(\frac{\mathrm{PV}^2 \mathrm{~T}^2}{\mathrm{n}}\) = \(\frac{\mathrm{N} / \mathrm{m}^2\left(\mathrm{~m}^3\right)^2(\mathrm{~K})^2}{\text { mole }}\)
= N × mole^-1m⁴k²
∴ The given quantity has SI units Nm⁴k² mole^-1.

Question 26.
In terms of Charles’ law explain why — 273°C is the lowest possible temperature.
Solution:
According to Charles law if we put the value of t = -273°C
in the equation V_t = V₀ \(\left[\frac{273.15+t}{273.15}\right]\).
In this case the volume of the gas becomes zero.
V₀ = Volume at 0° C
V_t = Volume at t° C

• This means the gas will not exist
• In fact all gases liquified before this temperature.

Question 27.
Critical temperature for carbon dioxide and methane are 31.1°C and – 81.9°C respectively. Which of these has
stronger intermolecular forces and why?
Solution:
Given Critical temperatures of CO₂, CH₄
T_C (CO₂) = 31.1°C
T_C (CH₄) = -81.9°C

• The gas with highest critical temperature value can be easily liquified because of high inter molecular forces.
  ∴ T_C(CO₂) is very high.
  So CO₂ gas liquified easily.
• ‘He’ gas has low T value so it is highly difficult to liquify.

Question 28.
Air is cooled form 25°C to 0°C. Calculate the decrease in rms speed of the molecules.
Solution:

Question 29.
Find the rms, most probable and average speeds of SO₂ at 27°c.
Solution:

Question 30.
Find the RMS. average and most probable speeds of O₂ at 27°c.
Solution:

u_average = 0.9213 × u_rms
= 0.9213 × 4.835 × 10⁴
= 4.455 × 10⁴ cm/sec.
u_mp = 0.8166 × u_rms
= 3.948 × 10⁴ cm/sec.

Question 31.
Give the values of Gas constant ‘R’ in different units.
Answer:
R = 0.0821 lit. atm. K^-1 .mol^-1
= 8.314 J.K^-1. mole^-1
= 1.987 (or) 2 cal.K^-1.mol^-1
= 8.314 × 10⁷ erg.K^-1.mol^-1