Andhra Pradesh BIEAP AP Inter 1st Year Chemistry Study Material 1st Lesson Atomic Structure Textbook Questions and Answers.
AP Inter 1st Year Chemistry Study Material 1st Lesson Atomic Structure
Very Short Answer Questions
Question 1.
What is the charge, mass, and charge-to-mass ratio of an electron?
Answer:
- Charge of an electron = – 1.602 × 10-19 coloumbs (or) -4.8 × 10-19 esu
- Mass of an electron = 9.1 × 10-28 gms
- Charge to mass ratio of an electron \(\left(\frac{\mathrm{e}}{\mathrm{m}}\right)\) i.e., specific charge = 1.758 × 1011 coloumbs/kg
Question 2.
Calculate the charge of one mole of electrons.
Answer:
One electron has charge – 1.602 × 10-19 coloumbs.
One mole of electrons has charge -6.023 × 1023 × 1.602 × 10-19
= 9.648846 × 104 = 96488.5 coloumbs.
![]()
Question 3.
Calculate the mass of one mole of electrons.
Answer:
Mass of electron = 9.1 × 10-31 kg (or) 9.1 × 10-28 gms.
One mole of electrons has mass 6.023 × 1023 × 9.1 × 10-31 = 54.8 × 10-8 = 5.48 × 10-7 kg.
Question 4.
Calculate the mass of one mole of protons. ”
Answer:
One proton has mass 1.672 × 10-27 kg
One mole protons has mass 6.023 × 1023 × 1.672 × 10-27
= 10.0704 × 10-4
= 1.00704 × 10-3 kg.
Question 5.
Calculate the mass of one mole of neutrons.
Answer:
One neutron has mass 1.675 × 10-27 kg
One mole neutrons has mass 6.023 × 1023 × 1.675 × 10-27
= 10.088 × 10-4
= 1.0088 × 10-3 kg.
Question 6.
How many neutrons and electrons are present in the nuclei of 6C13, 8O16, 12Mg24, 26Fe56 and 38Sr88.
Answer:

![]()
Question 7.
What is a black body ?
Answer:
The body which is perfect absorber and emmiter of all type of radiations incident on it is called a black body.
Question 8.
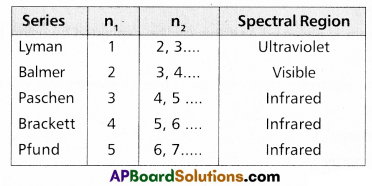
Which part of electromagnetic spectrum does Balmer series belong?
Answer:
Balmer series (n = 2) belongs to visible region of electromagnetic spectrum.
Question 9.
What is an atomic orbital?
Answer:
In an atom, the region around the nucleus where the probability of finding the electron is maximum is known as atomic orbital.
- From the value of magnitude of square of wave function (|\(\psi^2\)|) this region can be predicted.
Question 10.
When an electron is transferred in hydrogen atom from n = 4 orbit to n=5 orbit to which spectral series does this belong?
Answer:
- By the absorption of energy electron jumps from n = 4 orbit to n = 5 orbit.
- The electron present in n = 5 orbit emitts energy and return to n = 4 orbit. Hence the spectral lines series obtained in Brackett series (IR region)
Question 11.
How many “p” electrons are present in sulphur atom?
Answer:
Sulphur has electronic configuration – 1s2 2s2 2p6 3s2 3p4
∴ Sulphur has 10 ‘p’ electrons.
Question 12.
What are the values of principal quantum number (n) and azimuthal quantum number (l) for a 3d electron?
Answer:
For a 3d – electron principal quantum number (n) = 3 and
Azimuthal quantum number (l) = 2.
![]()
Question 13.
What is the complete symbol for the atom with the given atomic number (Z) and atomic mass (A)?
I) Z = 4, A = 9 ;
II) Z = 17, A = 35 ;
III) Z = 92, A = 233.
Answer:
I) Z = 4, A = 9 Complete symbol is 4Be9
II) Z = 17, A = 35 Complete symbol is 17Cl35
III) Z = 92, A = 233 complete symbol is 92U233.
Question 14.
Draw the shape of \(\mathrm{d}_{\mathrm{z}^2}\) orbital.
Answer:
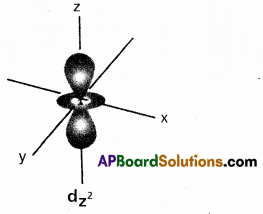
Question 15.
Draw the shape of dx2 – y2 orbital.
Answer:
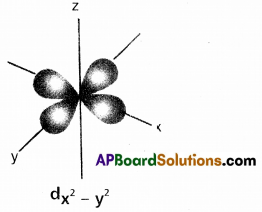
![]()
Question 16.
What is the frequency of radiation of wavelength 600nm?
Answer:
Formula:
\(v=\frac{c}{\lambda}\)
= \(\frac{3 \times 10^8}{6 \times 10^{-7}}\)
= \(\frac{1}{2} \times 10^{15}\)
= 0.5 × 1015 = 5 × 1014 sec-1
λ = 600 nm
= 600 × 10-9 m
= 6 × 10-7 m
C = 3 × 108 m/sec.
Question 17.
What is Zeeman effect?
Answer:
The splitting up of spectral lines in presence of strong external magnetic field is called as Zeeman effect.
Question 18.
What is Stark effect?
Answer:
The splitting of spectral lines in presence of strong electric field is called as Stark effect.
Question 19.
To which element does the following electronic configuration correspond?
I) 1s22s2 2p63s23p1
II) 1s22s22p63s23p6
III) 1s22s22p5
IV) 1s22s22p2.
Answer:
I) 1s22s2 2p6 3s2 3p1 (Atomic no. (Z) = 13) – Aluminium.
II) 1 s22s22p63s23p6(Atomic no. (Z) = 18) – Argon.
III) 1s22s22p5 (Atomic no. (Z) = 9) – Fluorine.
IV) 1s22s22p2 (Atomic no. (Z) = 6) – Carbon.
Question 20.
Electrons are emitted with zero velocity from a metal surface when it is exposed to radiation of wavelength 4000 A. What is the threshold frequency (\(v_0\))?
Answer:
Formula:
hv = hv0 + \(\frac{1}{2} m v^2\)
hv = hv0 + \(\frac{1}{2} m(0)^2\)
hv = hv0
λ = 4000 A
= 4 × 103 × 10-10 = 4 × 10-7 m.
V = 0
C = 3 × 108 m/sec.
⇒ v = v0
∴ v = \(\frac{\mathrm{C}}{\lambda}\) = \(\frac{3 \times 10^8}{4 \times 10^{-7}}\) = \(\frac{3}{4}\) × 1015
= 0.75 × 1015
= 7.5 × 1014 sec-1
Question 21.
Explain Pauli’s exclusion principle.
Answer:
Pauli’s exclusion principle:
According to this principle
“No two electrons in an atom can have the same set of four quantum numbers”. This can also be stated as “only two electrons may exist in the same orbital and these electrons must have opposite spins”.
This means that the two electrons can have the same value of three quantum numbers n, l and ml but have the opposite spin quantum number Ex : Consider ‘K’ shell of the atom having two electrons ![]()

Question 22.
What is Aufbaus principle ?
Answer:
Aufbau’s principle:
This principle states
“In the ground state of the atoms, the orbitals are filled in order of their increasing energies”. In other words electrons first occupy the lowest energy orbital available to them and enter into higher energy orbitals only after the lower energy orbitals are filled.
The order in which the orbitals are filled as follows :
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 4f < 5d < 6p < 7s
![]()
Question 23.
What is Hund’s rule ?
Answer:
Hund’s rule: This rule deals with the filling of electrons in degenerate orbitals. It states “Pairing of electrons in the orbitals belonging to the same subshell (p, d or f) does not take place until each orbital belonging to that subshell has got one electron each (i.e.,) all the orbitals are singly occupied”.
Since there are three ’p’, five ‘d’ and seven ‘f’ orbitals, therefore the pairing of electrons will start in the p, d and f orbitals with the entry of 4th, 6th and 8th electrons respectively.
Ex : ‘8O’ electronic configuration is
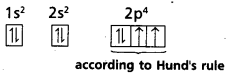
Question 24.
Explain Heisenberg’s uncertainty principle.
Answer:
Heisenberg uncertainty principle : “Simultaneous and exact determination of the position and momentum of a sub-atomic particle, like electron moving with high speed is impossible.”
If Δx and Δp represents the uncertainties in the position and momentum respectively. Then according to Heisenberg
Δx. Δp ≥ \(\frac{\mathrm{h}}{4 \pi}\) ——- (1)
The product of uncertainties in position (Δx) and momentum (Δp) of an electron cannot be less than \(\frac{h}{4 \pi}\). It can be equal or greater than \(\frac{h}{4 \pi}\).
Since momentum = mass x velocity, the equation (1) can be written as
Δx × m (Δv) ≥ \(\frac{\mathrm{h}}{4 \pi}\) = Δx × Δv ≥ \(\frac{\mathrm{h}}{4 \pi \mathrm{m}}\)
If the position is determined accurately Δx = 0 and Δv = ∝. That means the inaccuracy in measuring the velocity is ∝. If velocity is determined accurately Δv = 0 and Δx = ∝.
Question 25.
What is the wavelength of an electron moving with a velocity of 2.0 × 107m/s ?
Answer:
Formulae:
λ = \(\frac{h}{m v}\)
= \(\frac{6.625 \times 10^{-34}}{9.1 \times 10^{-31} \times 2 \times 10^7}\)
= 0.3640 × 10-34 × 10+24
= 0.3640 × 1010 m
= 0.3640 A
h = 6.625 × 10-34 J.Sec
m = 9.1 × 10-31 kg
V = 2.0 × 107 m/sec.
Question 26.
An atomic orbital has n = 2, what are the possible values of l and ml?
Answer:
For n = 2, l values are 0, 1
For l = 0 → ml = 0
For l = 1 → ml = -1, 0, +1.
![]()
Question 27.
Which of the following orbitals are possible? 2s, 1p, 3f, 2p.
Answer:
2s, 2p orbitals are possible among 2s, 1p, 3f, 2p and 1 p, 3f orbitals are not possible.
Question 28.
The static electric charge on the oil drop is – 3.2044 × 10-19 C. How many electrons are present on it?
Answer:
Given static electric charge on oil drop = – 3.2044 × 10-19 C
Charge of electron = – 1.602 × 10-19 C.
Number of electrons present =
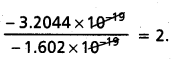
Question 29.
Arrange the following type of radiation in increasing order of frequency:
(a) X – rays
(b) visible radiation
(c) microwave radiation and
(d) radiation from radio waves.
Answer:
Increasing order of frequency of given radiations is
Radio waves < Micro waves < Visible radiation < X – rays.
Question 30.
How many electrons in an atom may have n = 4 and ms = +1/2 ?
Answer:
For n = 4 → l values are 0, 1, 2, 3
l = 0 → s contains 1 electron with ms = + 1/2
l = 1 → p contains 3 electron with ms = + 1/2
l = 2 → d contains 5 electron with ms = + 1/2
l = 3 → f contains 7 electron with ms = + 1/2
∴ Total no.of electrons with ms = +1/2 for n = 4
= 1 + 3 + 5 + 7 = 16.
![]()
Question 31.
How many sub-shells are associated with n = 5 ?
Answer:
For n = 5
l values are 0, 1, 2, 3, 4
l = 0 → s – orbital
l = 1 → p — orbital
l = 2 → d – orbital
l = 3 → f – orbital
l = 4 → g — orbital
→ Five subshells are associated with n = 5.
Question 32.
Explain the particle nature of electromagnetic radiation.
Answer:
- According to earlier days concepts light was supposed to be made of particles. This assumption was made by Newton in his corpuscular theory. He called the particles as corpuscales.
- The particle nature of light explains the black body radiations and photo electric effect satisfactorily.
- The particle nature of light could not satisfactorily explains the phenomenon of diffraction and Interferance.
Question 33.
Explain the significance of Heisenberg’s Uncertainty principle.
Answer:
Significance of Uncertainty Principle:
- This principle rules out the existence of definite paths or trajectories of electrons and other similar particles.
- This principle is significant only for motion of microscopic objects, and is negligible for that of macroscopic objects.
- In dealing with milligram size or heavier objects, the associated uncertainties are hardly of any real consequence.
Question 34.
What series of lines are observed in hydrogen spectra?
Answer:
The series of lines observed in hydrogen spectra are

Additional Answer Questions
Question 35.
How many newtrons and electrons are present in the nuclei of \({ }_6 C^{13}\), \({ }_8 \mathrm{O}^{16}\), \({ }_{12} \mathrm{Mg}^{24}\), \({ }_{26} \mathrm{Fe}^{56}\), \({ }_{38} \mathrm{Sr}^{88}\)
Answer:
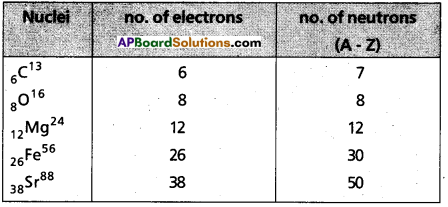
Additional Problems
Question 36.
Calculate the wave no. and wave length of first line of lyman series.
Answer:

![]()
Question 37.
Calculate the wave no. of and wave length of first line of Balmer series.
Answer:

Short Answer Questions
Question 38.
What is the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from an energy level with n = 5 to an energy level with n = 3 ?
Answer:
Formulae:

R = 1,09,677 cm-1
n1 = 3
n2 = 5.
\(\bar{v}\) = 7799.25 cm-1
λ = \(\frac{1}{\bar{v}}\) = \(\frac{1}{7799.25}\) = 1.2821 × 10-4 cm
Question 39.
An atom of an element contains 29 electrons and 35 neutrons. Deduce
- the number of protons and
- the electronic configuration of the element.
Answer:
Given no.of electrons ’29’, ∴ Z = 29
- So, no.of protons = 29
- Electronic configuration of the element (Z = 29)
= 1s22s22p23s23p64s13d10 [anamalous electronic configuration]
Question 40.
Explain giving reasons, which of the following sets of quantum numbers are not possible.
a) n = 0, l = 0, ml = 0, ms = +\(\frac{1}{2}\)
b) n = 1, l = 0, ml = 0, ms = –\(\frac{1}{2}\)
c) n = 1, l = 1, ml = 0, ms = +\(\frac{1}{2}\)
d) n = 2, l = 1, ml = 0, ms = +\(\frac{1}{2}\)
e) n = 3, l = 3, ml = – 3, ms = +\(\frac{1}{2}\)
f) n = 3, l = 1, ml = 0, ms = +\(\frac{1}{2}\)
Answer:
Following set of quantum numbers are not possible.
a) n = 0, l = 0, ml = 0, ms = +\(\frac{1}{2}\)
Reason:
‘n’ is principal quantum number, whose values are from 1 to n. The value of ‘n’ never equal to zero. But given n = 0.
c) n = 1, l = 1, ml = 0, ms = +\(\frac{1}{2}\)
Reason:
Values of ‘l’ are from 0 to (n – 1).
If n = 1 then the value of ‘l’ is zero not equal to ‘1’.
e) n = 3, l = 3, ml = – 3, ms = +\(\frac{1}{2}\)
Reason:
If n = 3, possible values of ‘l’ are 0, 1, 2, but not equal to ‘3’.
Question 41.
Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
Answer:
Consider the Bohr’s angular momentum equation.
mvr = \(\frac{\mathrm{nh}}{2 \pi}\)
i.e The angular momentum of an electron is integral multiple of ‘\(\frac{\mathbf{h}}{2 \pi}\)‘
mvr = \(\frac{\mathrm{nh}}{2 \pi}\)
2πr = \(\frac{\mathrm{nh}}{\mathrm{mv}}\)
According to de-Broglie’s wavelength λ = \(\frac{h}{m v}\)
2πr = \(n\left(\frac{h}{m v}\right)\)
2πr = nλ.
Thus the circumference of the Bohr orbit is integral multiple of de-Broglie’s wave length.
Question 42.
The longest wavelength doublet absorption transition is observed at 589.0 and 589.6 nm. Calculate the frequency of each transition and energy difference between two excited states.
Answer:
Given largest wave length doublet absorption transition is observed at 589.0 and 589.6 nm.
∴ \(v_1=\frac{c}{\lambda_1}\)
= \(\frac{3 \times 10^8}{589 \times 10^{-9}}\) = 0.005093 × 10+7
= 5.093 × 1014 sec-1
λ1 = 589 × 10-9 m
∴ \(v_2=\frac{c}{\lambda_2}\)
= \(\frac{3 \times 10^8}{589.6 \times 10^{-9}}\)
= 0.005088 × 1017
= 5.088 × 1014 sec-1
λ1 = 5.089 × 10-9 m
Energy difference between two states = h[\(v_1\) – h\(v_2\)]
= h[\(v_1\) – \(v_2\)]
= 6.625 × 10-34[5.093 × 10-14 – 5.088 × 1014]
= 6.625 × 10-34 × 0.005 × 1014
= 0.0331 × 10-20 J.
![]()
Question 43.
What are the main features of quantum mechanical model of an atom?
Answer:
Important features of quantum mechanical model of atom:
- The energy of electrons in an atom is quantized (it can only have certain specific values).
- The existence of quantized electronic energý levels is a direct result of the wave like properties at electrons and are allowed solution at Schrodinger wave equation.
- All the information about the electron in an atom is contained in its orbital wave function ‘Ψ’ and quantum mechanics makes it possible to extract this information from “Ψ’.
- The path of the electron can never be determined accurately. Therefore, we find only the probability of the electron at different points in space, around an atom.
- The probability of finding an electroñat a point within an atom is proportional to the square of the orbital wave function i.e., \(|\Psi|^2\) at that point. \(|\Psi|^2\) is known as probability density and is always positive. From the value of \(|\Psi|^2\) at different points with in the atom, it is possible to predict the region around the nucleus where electron will most probably be found.
Question 44.
What is a nodal plane? How many nodal planes are possible for 2p – and 3d – orbitals?
Answer:
The plane at which the probability of finding the electron is zero is called as nodal plane.
- For 2p orbitaIs one nodal plane is possible for each ‘p’ orbital.
- For 3d orbitais two nodal planes are possible for each ‘d’ orbital.
Question 45.
The Lyman series occurs between 91.2 nm and 121.6 nm, the Balmer series occurs between 364.7 nm and 656.5 nm and the Paschen series occurs between 820.6 nm and 1876 nm. Identify the spectral regions to which these wavelengths correspond?
Answer:
In electromagnetic spectrum,
a) 91.2 – 121.6 nm (Lyman senes) corresponds to u.v. region.
b) 364.7 – 656.5 nm (Balmer series) corresponds to visible region.
c) 820.6 – 1876 nm (Paschen series) corresponds to I.R. region.
![]()
Question 46.
How are the quantum numbers n, l, ml, for hydrogen atom obtained?
Answer:
Electronic configuration of hydrogen is 1s1
For ns1
Principal quantum no. (n) = 1
Azimuthal quantum no. (l) = 0
Magnetic quantum no. (ml) = 0
and Spin quantum no. (ms) = + 1/2
Question 47.
A line in Lyman series of hydrogen atom has a wavelength of 1.03 × 10-7 m. What is the initial energy level of the electron?
Answer:
Given λ= 1.03 × 10-7 m = 1.03 × 10-5 cm
n2 = 1 (for Lyman series)
We have, R = 109677 cm-1
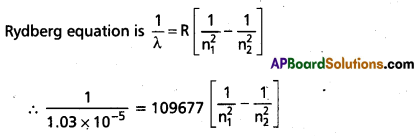
⇒ n2 = 3 (i.e.,) original energy level of electron is 3.
Question 48.
If the position of the electron is measured within an accuracy of ±0.002 nm. Calculate the uncertainty in the momentum of the electron.
Answer:
Formulae:
Δx × Δp = \(\frac{h}{4 \pi}\)
Δp = \(\frac{h}{\Delta x \times 4 \pi}\)
= \(\frac{6.625 \times 10^{-34}}{4 \times 3.14 \times 2 \times 10^{-12}}\)
= 0.2637 × 10-22
= 2.637 × 10-23 J/m.
Δx = 0.002 nm
= 2 × 10-3 × 109 m
= 2 × 10-12 m
h = 6.625 × 10-34 J.sec.
∴ Uncertainity in momentum of electron = 2.637 × 10-23 J/m.
Question 49.
If the velocity of the electron is 1.6 × 106 m/s-1. Calculate de Brogue wavelength associated with this electron.
Answer:
Formulae:
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\)
= \(\frac{6.625 \times 10^{-34}}{9.1 \times 10^{-31} \times 1.6 \times 10^6}\)
= 0.455 × 10-9 m
= 0.455 nm.
v = 1.6 × 106 m/sec
h = 6.625 × 10-34 J.sec
m = 9.1 × 10-31 Kg.
![]()
Question 50.
Explain the difference between emission and absorption spectra. (A.P. Mar. ‘15)
Answer:
Emission spectrum
- It is produced by analysing the radiant energy emitted by an excited substance.
- It consists of bright lines on dark back ground.
- Produced due to the emission of energy by electrons.
- Emission spectra contains bright ineson dark back ground.
Absorption spectrum
- It is produced when white light is passed through a substance and the transmitted light is analysed by a spectrograph.
- It consists of dark lines on bright background.
- Produced due to the adsorption of energy by electrons.
- Absorption spectra contains dark lines on bright back ground.
Question 51.
The quantum numbers of electrons are given below. Arrange them in order of increasing energies.
a) n = 4, l = 2, ml = -2, ms = +\(\frac{1}{2}\)
b) n = 3, l = 2, ml = -1, ms = –\(\frac{1}{2}\)
c) n = 4, l = 1, ml = 0, ms = +\(\frac{1}{2}\)
d) n = 3, l = 1, ml = -1, ms = –\(\frac{1}{2}\)
Answer:
a) n = 4, l = 2, → 4d
b) n = 3, l = 2, → 3d
c) n = 4, l = 1, → 4p
d) n = 3, l = 1, → 3p
∴ 3p < 3d < 4p < 4d
According (n + l) values
Hence d < b < c < a is order of increasing energy.
![]()
Question 52.
The work function for Cesium atom is 1.9 eV. Calculate the threshold frequency of the radiation. If the Cesium element is irradiated with a wavelength of 500 nm, calculate the kinetic energy of the ejected photoelectron?
Answer:
Case-I
Photo electric effect equation is
hv = hv0 + 1/2 mv2
w = hv0

Case-II
Photo electric effect equation is
E = \(\frac{\mathrm{hc}}{\lambda}\)
= \(\frac{6.625 \times 10^{-34} \times 3 \times 10^8}{5 \times 10^{-7}}\)
= \(\frac{19.878 \times 10^{-26}}{5 \times 10^{-7}}\)
= 3.9756 × 10-19 J.
Given work function hv0 = 1.9 ev
= 1.9 × 1.602 × 10-19J.
Kinetic Energy (KE) = \(\frac{1}{2} m v^2\)
From Photo electric effect
\(\frac{1}{2} m v^2\) = hv – hv0
K.E. = 3.9756 × 10-19 × 1.602 × 10-19
= 3.9756 × 10-19 – 3.0438 × 10-19 = 0.9318 × 10-19 = 9.318 × 10-20J.
Question 53.
Calculate the wavelength for the emission transition if it starts from the orbit having radius 1.3225 nm and ends at 211.6 pm. Name the series to which this transition belongs and the region of the spectrum.
Answer:
Given the radius of orbit from which it started = 1.35225 × 10-9 m = 1 3.225Å
In general radius of orbit = 0.529 × n2Å
n2 = \(\frac{13.225}{0.529}\) = 25
n2 = 25 ⇒ n = 5
Given that the
Radius of orbit at which the transition ended = 211.6 pm
= 211.6 × 10-12m
= 2.116A
Similarly as above
n2 = \(\frac{2.116}{0.529}\) = 4
n2 = 4 ⇒ n = 2
∴ transition takes place from n = 5 to n = 2 level
∴ spectral lines are obtained in Balmer series (visible region)
Question 54.
Explain the difference between orbit and orbital.
Answer:
Orbit
- A circular path which is present around the nucleus in which electrons revolve is called as orbit.
- Orbits are circular and are non directional paths.
- The maximum no.of electrons in any orbit is given by the formula 2n2 (n = orbit number).
Orbital
- The 3 – dimension space where the probability of finding the electron is maximum around the nucleus is called as orbital.
- These have definite shape and these are directional except’s orbital.
- Each orbital can occupy a maximum of two electrons.
![]()
Question 55.
Explain photoelectric effect.
Answer:
The ejection of electrons from a metal surface, when the radiations of suitable frequency strikes the metal surface is called photoelectric effect.
Explanation using Einstein’s quantum theory:
1) To explain photoelectric effect, Einstein utilised Quantum theory.
2) When a photon strikes metal surface, it uses some part of its energy to eject the electron from the metal atom. The remaining part of the total energy is given to the ejected electrons in the form of kinetic energy.
Hence we can write hv = W + KE ⇒ hv = hv0 + \(\frac{1}{2} m_e v^2\)
where hv = energy of photon,
v0 = Threshold frequency,
me = mass of electron
W = energy required to overcome the attractive forces on the electron in the metal (work function)
KE = kinetic energy of ejected electron,
V = Velocity of ejected electron.
3) If a photon of sufficient energy struck the metal surface and could eject the electron. But if a photon has insufficient energy, it cannot eject the electron from the metal.
eg. : A photon of violet light [high frequency] can eject the electrons from the surface of potassium but a photon of red light [low frequency] cannot eject the electrons.
Question 56.
Explain Rutherford’s nuclear model of an atom. What are its drawbacks?
Answer:
Rutherford’s Planetary model: Rutherford drew some conclusions regarding the structure of atom.
- Most of the space in the atom is empty (as most of the α – particles passed through the foil undeflected).
- A few — positive charges were deflected. The deflection must be due to enormous repulsive force showing that the positive charge of the atom is not spread throughout the atom as Thomson predicted. The positive charge is concentrated in a very small volume. Which is responsible for the deflection of α — particles.
On the basis of the above observations. Rutherford proposed the nuclear model. According to his model.
- The positive charge in the atom is concentrated in the small dense portion, called the NUCLEUS.
- The nucleus is surrounded by the electrons that move around it in circular paths called the ORBITS. Thus Rutherford’s model resembles the solar system.
- Electrons and the nucleus are held together by electrostatic forces of attraction.
Drawbacks of Rutherford model:
1. Rutherford’s atomic model of an atom is like a small scale solar system. This similarity suggests that electrons should move around the nucleus in well defined orbits. However, when a body is moving, it undergoes acceleration. According to electromagnetic theory, charged particles, when accelerated, should emit radiation. Therefore, an electron in an orbit will emit radiation, thus the orbit will continue to shrink. But this does not happen. Thus Rutherford’s model cannot explain the stability of the atom.
2. If we assume that electrons as stationary around the nucleus, the electrostatic attraction between the nucleus and the electrons would pull the electrons towards the nucleus to form a miniature version of Thomson’s model.
3. Rutherford model does not explain the electronic structure of the atom i.e., how the electrons are distributed around the nucleus and what are the energies of these electrons.
Before studying further developments that lead to the formulation of various atomic models, it is necessary to study about light and its nature.
Question 57.
Explain briefly the Planck’s quantum theory.
Answer:
The postulates. of Planck’s quantum theory are
a) The emission of radiation is due to vibrations of charged particles (electrons) in the body.
b) The emission is not continuous but in discrete packets of energy called quanta. This emitted radiation propagates in the form of waves.
c) The energy (E) associated with each quantum for a particular radiation of frequency V is given by E = hv, Here ‘h’ is Planck’s constant.
d) A body can emit or absorb either one quantum (hv) of energy or some whole number multiple of it. Thus energy can be emitted or absorbed as hv, 2hv, 3hv etc., but not fractional values. This is called quantisation of energy.
e) The emitted radiant energy is propagated in the form of waves.
f) Values of Planck’s constant in various units:
h = 6.6256 × 10-27 erg.sec (or) g cm2s-1
= 6.6256 × 10-34J.s (or) kg m2s-1 = 1.58 × 10-34 cal.s.
Success of Planck’s quantum theory: This theory successfully explains the black body radiations. A black body is a perfect absorber and also a perfect radiator of radiations.
![]()
Question 58.
What are the postulates of Bohr’s model of hydrogen atom? Discuss the importance of this model to explain various series of line spectra In hydrogen atom. (T.S. Mar. ‘16)(A.P. Mar.’15. ‘13)
Answer:
Niels Bohr quantitatively gave the general features of hydrogen atom structure and it’s spectrum. His theory is used to evaluate several points in the atomic structure and spectra.
The postulates of Bohr atomic model for hydrogen as follows
Postulates : –
- The electron in the hydrogen atom can revolve around the nucleus in a circular path of fixed radius and energy. These paths are called orbits (or) stationary states. These circular orbits are concentric (having same center) around the nucleus.
- The energy of an electron in the orbit does not change with time.
- When an electron moves from lower stationary state to higher stationary state absorption of energy takes place.
- When an electron moves from higher stationary state to lower stationary state emission of energy takes place.
- When an electronic transition takes place between two stationary states that differ in energy by ΔE is given by
ΔE = E2 – E1 = hv
∴ The frequency of radiation absorbed (or) emitted v = \(\frac{E_2-E_1}{h}\) E1 and E2 are energies of lower, higher energy states respectively. - The angular momentum of an electron is given by mvr = \(\frac{\mathrm{nh}}{2 \pi}\)
An electron revolve only in the orbits for which it’s angular momentum is integral multiple of \(\frac{\mathrm{h}}{2 \pi}\)
Line spectra of hydrogen, Bohr’s Theory:
- In case of hydrogen atom line spectrum is observed and this can be explained by using Bohr’s Theory.
- According to Bohr’s postulate when an electronic transition takes place between two stationary states that differ in energy is given by
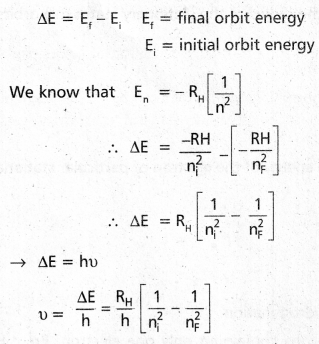

- In case of absorption spectrum nf > ni → energy is absorbed (+ve) energy is absorbed (+Ve)

- In case of emission spectrum ni > nf → energy is emitted (- Ve)
- Each spectral line in absorption (or) emission spectrum associated to the particular transition in hydrogen atom
- In case of large no.of hydrogen atoms large no.of transitions possible they rsults in large no.of spectral lines.
The series of lines observed in hydrogen spectra are
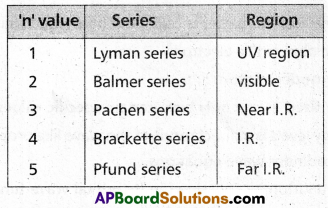
Question 59.
Explain the success of Bohr’s theory for hydrogen atom.
Answer:
Succes of Bohrs Theory for hydrogen atom:
- Bohr’s theory gave the information about the principal quantum number. Principal quantum number represents the stationary states. (n = 1, 2, 3 integral numbers)
- Bohr’s theory gave the information about the radius of the stationary states (or) orbits.
r = 0.529 × n2 A (or)
r = 52.9 × n2 pm
\(\left[r=\frac{n^2 h^2}{4 \pi^2 m e^2}\right]\) (for hydrogenation) - This theory gave the information about the energy of the electron of particular stationary state.
En = -RH \(\left[\frac{1}{n^2}\right]\)n = 1, 2, 3,……
RH = Ryd berg constant
= 1,09,677 cm-1. - This theory explained the line spectra of hydrogenation.
- This theory can also be applicable to the ions containing only one electron. Eg. : He+, Li+2, Be+3….
- This theory can also gave information about velocity of electrons moving in the orbits.
Question 60.
What are the consequences that lead to the development of quantum mechanical model of an atom?
Answer:
Consequences that lead to development of quantum mechanical model of an atom are as follows.
- Clàssical mechanics successfully explained the motion of macro scopic objects.
Eg: Falling stone, Planets etc.,. - Classical mechanics failed to explain the motion of microscopic objects like electrons, atoms, molecules etc.
- Classical mechanics ignores the concept of dual behaviour of matter and especially for sub atomic particles
Quantum mechanics:
The Branch of science deals with the dual behaviour of matter is called quantum mechanics. - This deals with the motions of microscopic objects like electron.
Important features of quantum mechanical model of atom:
- The energy of electrons in an atom is quantized (it can only have certain specific values).
- The existence of quantized electronic energy levels is a direct result of the wave like properties at electrons and are allowed solution at schrodinger wave equations.
- All the information about the electron in an atom is contained in its orbital wave function ‘\(\Psi^{\prime}\) and quantum mechanics makes it possible to extract this information from ‘\(\Psi^{\prime}\).
- The path of the electron can never be determined accurately. Therefore, we find only the probability of the electron at different points in space, around an atom.
- The probability of finding an electron at a point within an atom is proportional to the square of the orbital wave function i.e., \(|\Psi|^2\) at that point. \(|\Psi|^2\) is known as probability density and is always positive. From the value of \(|\Psi|^2\) at different points with in the atom, it is possible to
predict the region around the nucleus where electron will most probably be found.
![]()
Question 61.
Explain the salient features of quantum mechanical model of an atom.
Answer:
Important features of quantum mechanical model of atom:
- The energy of electrons in an atom is quantized (it can only have certain specific values).
- The existence of quantized electronic energy levels is a direct result of the wave like properties at electrons and are allowed solution at schrodinger wave equations.
- All the information about the electron in an atom is contained in its orbital wave function ‘\(\Psi^{\prime \prime}\) and quantum mechanics makes it possible to extract this information from \(\Psi^{\prime \prime}\).
- The path of the electron can never be determined accurately. Therefore, we find only the probability of the electron at different points in space, around an atom.
- The probability of finding an electron at a point within an atom is proportional to the square of the
orbital wave function i.e., \(|\Psi|^2\) at that point. \(|\Psi|^2\) is known as probability density and is always positive. From the value of \(|\Psi|^2\) at different points with in the atom, it is possible to predict the region around the nucleus where electron will most probably be found.
Question 62.
What are the limitations of Bohr’s model of an atom?
Answer:
Limitations:
- Spectra of multielectron atoms: Bohr’s theory could explain the spectra of Hydrogen and single electron species like He+, Li2+, Be3+, but it fails to explain the spectra of multielectron atoms.
- Fine structure: It fails to explain this fine structure of Hydrogen atom.
- Splitting up of spectral lines : The theory fails to explain Zeeman effect and Stark effect.
The splitting up of spectral lines when an atom is subjected to strong magnetic field is called Zeeman effect.
The splitting up of spectral lines when an atom is subjected to strong electric field is called Stark effect. - Flat model: Bohr’s theory gives a flat model of the orbits. Bohr’s theory predicts definite orbits for electrons considering them as particles. But according to de Brogue electron has both wave nature and particle nature. Bohr’s theory cannot explain this dual role.
- It fails to support the uncertainty principle proposed by Heisenberg.
- It could not explain the ability of atoms to form molecules by chemical bonds.
Question 63.
What are the evidences in favour of dual behaviour of electron?
Answer:
- The particle nature of light explains the phenomenon of blackbody radiations and photo electric effect but it could not explain about wave nature of light.
- Wave nature of light explains the phenomenon of interference and diffraction.
- So, light has dual nature i.e it behaves as a wave (or) as a stream of particles.
- According to de-Broglie, light has dual behaviour i.e both particle and wave nature.
de-Broglies gave the following relationship
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{h}{p}\)
λ = wave length
P = momentum - Heisen bergs uncertainty principle also a consequence of dual behaviour of matter and radiation.
Statement :— It is impossible to determine simultaneously, the exact momentum and exact position of a small particle like lectron.
Δx × Δp ≥ \(\frac{h}{4 \pi}\)
Δx = uncertainty in position
Δp = uncertainty in momentum
![]()
Question 64.
How are the quantum numbers n, l and ml, arrived at? Explain the significance of these quantum numbers. (A.P. Mar. ‘16)(T.S. Mar. ‘15, ‘14)
Answer:
- In general a large no.of orbitals are possible in an atom.
- These orbitaIs are distinguished by their size, shape and orientation.
- An orbital of smaller size means there is more chance to find electron near the nucleus.
- Atomic orbitals are precisely distinguished by quantum numbers. Each orbital is designated by three major quantum numbers.
1) Principal quantum number (n)
2) Azimuthal quantum number (l)
3) Magnetic quantum number (m)
1) Principal quantum number : The principal quantum number was introduced by Neils Bohr. It reveals the size of the atom (main energy levels). With increase in the value of ‘n’ the distance between the nucleus and the orbit also increases.
It is denoted by the letter ‘n’. It can have any simple integer value 1, 2, 3, ……. but not zero. These are also termed as K, L, M, N etc.
The radius and energy of an orbit can be determined basing on ”n” value.
The radius of nth orbit is rn = \(\frac{n^2 h^2}{4 \pi^2 m e^2}\)
The energy of nth orbet is En = \(\frac{-2 \pi^2 m e^4}{n^2 h^2}\)
2) Azimuthal quantum number: It was proposed by Sommerfeld. it is also known as angular momentum quantum number or subsidiary quantum number.
it indicates the shapes of orbitals. It is denoted by ‘l’. The values of ‘l’ depend on the values of ‘n’, ‘l’ has values ranging from ‘0 to (n – 1) i.e.. l = 0, 1, 2,….. (n – 1). The maximum number of electrons present in the subshells s, p, d, f are 2, 6, 10, 14 respectively.

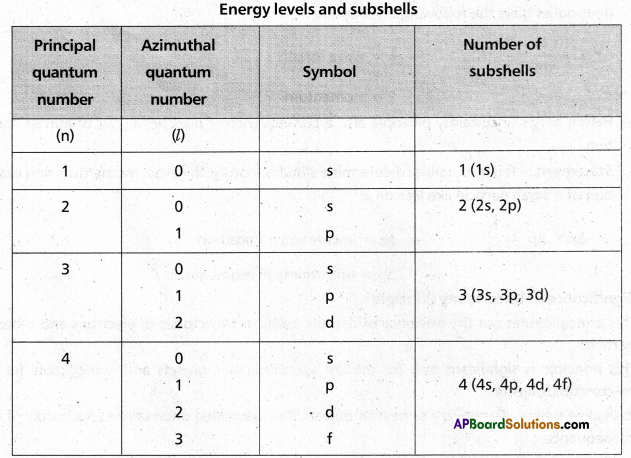
3) Magnetic quantum number: It was proposed by Lande. It shows the orientation of the orbitals in space. ‘p’ — orbital has three orientations. The orbital oriented along the x-axis is called px orbital, along the y-axis is called py -orbital and along the z-axis is called pz orbital. In a similar way d – orbital has five orientations. They are dxy, dyz, dzx, dx2 – y2 and dz2. It is denoted by ‘m’. Its values depends on azimuthal quantum number, ‘m’ can have all the integral values from -l to +l including zero. The total number of ‘m’ values are (2l + 1).

Question 65.
Explain the dual behaviour of matter. Discuss its significance to microscopic particles like electrons.
Answer:
- The particle nature of light explains the phenomenon of blackbody radiations and photo electric effect but it couldnot explain about wave nature of light.
- Wave nature of light explains the phenomenon of interference and diffraction.
- So, light has dual nature i.e it behaves as a wave (or) as a stream of particles.
- According to de-Broglie light has dual behaviour i.e both particle and wave nature.
de-Broglies gave the following relationship
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{h}{p}\)
λ = wavelength
P = momentum - Heisen bergs uncertainty principle also a consequence of dual behaviour of matter and radiation.
Statement :— It is impossible to determine simultaneously, the exact momentum and exact position of a small particle like electron.
Δx × Δp ≥ \(\frac{h}{4 \pi}\) = uncertainty in position
Δx = uncertainty in position
Δp = uncertainty in momentum
Significance of Uncertainty Principle:
- This principle rules out the existence of definite paths or trajectories of electrons and other similar
particles. - This principle is significant only for motion of microscopic objects and is negligible for that of macroscopic objects.
- In dealing with milligram size or heavier objects, the associated uncertainties are hardly of any real consequence.
Question 66.
What are various ranges of electromagnetic radiation ? Explain the characteristics of electromagnetic radiation.
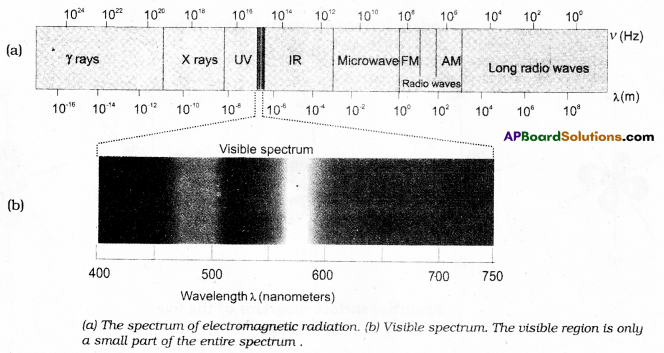
(or)
Explain diagrammatically the boundary surfaces for three 2p orbitais and five 3d
Answer:
Electromagnetic radiation : When electrically charged particle is accelerated alternating electric and magnetic fields are produced and transmitted. These fields are transmitted in the form of waves called electromagnetic waves or electromagnetic radiation.
Important Characteristics of a wave:
1) These are produced by oscillating charged particles in a body.
2) These radiations can pass through vacuum also. So medium for transmission is not required.
3) Velocity (c) : It is defined as the linear distance travelled by the wave in one second.
Units : cm sec-1 (or) m see-1
All kinds of electromagnetic waves have the same velocity.
(3 × 108 m sec-1 or 3 × 1010 cm sec-1)
4) Wavelength (λ) : It is defined as the distance between any two successive crests or troughs of wavez.
Units:A ; m ; cm ; nm or pm 1 A° = 10-10 m
1 nm = 10-9 m = 10-7 cm
1 pm = 10-12m.
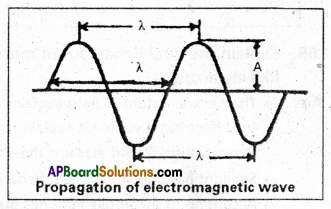
5) Frequency (v): It is defined as the number of waves passing through a point in one second.
Units: Hertz (Hz); cycles sec-1 or sec-1.
v = \(\frac{c}{\lambda}\)
6) Wave number (\(\bar{v}\)): It is defined as the number of waves present in one unit length. It is equal
to the reciprocal of the wavelength.
\(\bar{v}=\frac{1}{\lambda}=\frac{v}{c}\)
Relation between wavelength and frequency :
c = v × λ ⇒ v = \(\frac{c}{\lambda}\)
7) Amplitude (A) is the height of the crest (or) depth of through of a wave, It determines intensity (or) brightness of the wave.
Question 67.
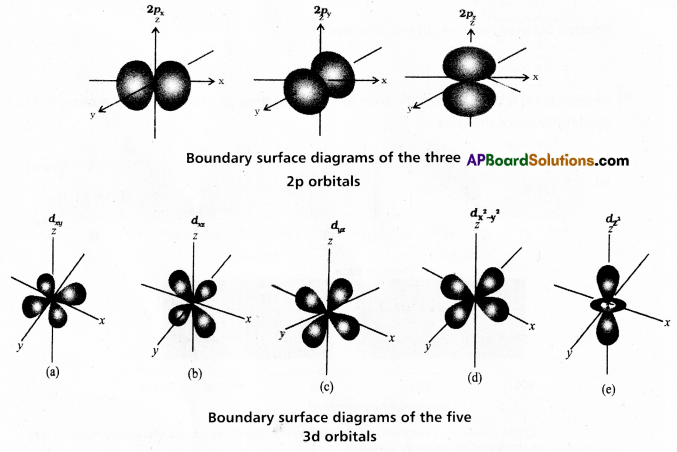
Define atomic orbital. Explain the shapes of s, p and d orbitals with the help of diagrams.
Answer:
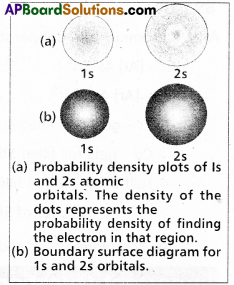
Atomic orbital : A three dimensional space around the nucleus in an atom. Where the probability of finding an electron is maximum (i.e.,) \(\Psi^2\) is maximum is called an atomic orbital.
Shapes of orbitals:
a) s – orbital : Boundary surface diagram for ‘s’ orbital is spherical in shape, ‘s – orbitals are spherically symmetric (i.e.,) the probability of finding the electron at a given distance is equal in all directions.
b) p – orbitals : p – orbital consists of two sections called lobes that are either side of the plane that passes through the nucleus. The size, shape and energy of the three orbitals are identical. They differ only in the orientation. These are mutually perpendicular to each other and oriented along x, y and z axes. Each p-orbital is of dumb-bell shape.
c) d – orbitals: Five d-orbitals are designated as dxy, dyz, dzx, dx2 – y2 and dz2. The shapes of first four d – orbitals are similar to each other of double dumb-bell whereas that of the fifth one ddz2 is different from others, but all five d-orbitals are equivalent in energy.
Question 68.
Illustrate the reasons for the stability of completely filled and half filled subshells.
Answer:
Chromium and Copper shows anamalous electronic configurations
Cr – [Ar] 4s1 3d5
Cu – [Ar] 41 3d10
- Cr — gets half filled 3d— shell electronic configuration.
- Cu — gets full filled 3d— shell electronic configuration.
- Half filled and full filled subshells are more stable than others.
Causes of Stability of Completely filled and Half filled Sub-shells
The completely filled and half filled sub-shells are stable due to the following reasons :
1. Symmetrical distribution of electrons : It is well known that symmetry leads to stability. The completely filled or half filled subshells have symmetrical distribution of electrons in them and are therefore more stable. Electrons in the same subshell (here 3d) have equal energy but different spatial distribution, Consequently, their shielding of one another is relatively small and the electrons are more strongly attracted by the nucleus.
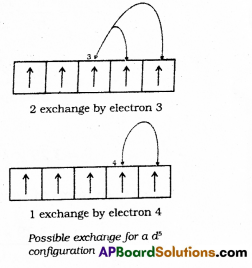
2. Exchange Energy: The stabilizing effect arises whenever two or more electrons with the same spin are present in the degenerate orbitals of a subshell. These electrons tend to exchange their positions and the energy released due to this exchange is called exchange energy. The number of exchanges that can take place is maximum when the subshell is either half filled or completely filled.
As a result the exchange energy is maximum and so is the stability.
The extra stability of half-filled and completely filled subshell is due to:
- relatively small shielding,
- smaller coulombic repulsion energy and
- larger exchange energy.
Question 69.
Explain emission and absorption spectra. Discuss the general description of line spectra in hydrogen atom.
Answer:
Emission spectrum:
- It is produced by analysing the radiant energy emitted by an excited substance.
- It consists of bright lines on dark background.
- Produced due to the emission of energy by electrons.
- Emission spectra contains bright lines on dark background.
Absorption spectrum:
- It is produced when white light is passed through a substance and the transmitted light is analysed by a spectrograph.
- It consists of dark lines on bright background.
- Produced due to the adsorption of energy by electrons.
- Absorption spectra contains dark lines on bright background.
Line spectra of Hydrogen — Bohrs Theory:- In case of hydrogen atom line spectrum is observed and this can be explained by using Bohr’s Theory.
- According to Bohrs postulate when an electronic transition takes place between two stationary states that differ in energy is given by
ΔE = Ef – Ei
Ef = final orbit energy
Ei = initial orbit energy

In terms of wave numbers
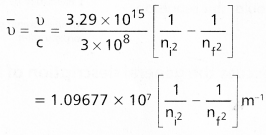

- In case of absorption spectrum nf > ni → energy is absorbed (+ Ve)
- In case of emission spectrum ni > nf → energy is emitted (- Ve)
- Each spectral line in absorption (or) emission spectrum associated to the particular transition in hydrogen atom
- In case of large no.of hydrogen atoms large no.of transitions possible they results in large no.of spectral lines.
The Spectral Lines for Atomic Hydrogen
Solved Problems
Question 1.
Calculate the num Notons, neutrons and electrons species?
Solution:
In this case, \({ }_{35}^{80} \mathrm{Br}\), Z = 35, 80, species is neutral
Number of protons = number of electrons = Z = 35
Number of neutrons = 80 – 35 = 45, Mass number (A) = number of protons (Z) + number of neutrons (n).
Question 2.
The number of electrons, protons and neutrons in a species are equal to 18, 16 and 16 respectively. Assign the proper symbol to the species.
Solution:
The atomic number is equal to number of protons =16. The element is sulphur (S).
Atomic mass number = number of protons + number of neutrons = 16 + 16 = 32
Species is not neutral as the number of protons is not equal to electrons. It is anion (negatively charged) with charge equal to excess electrons = 18 – 16 = 2.
Symbol is \(\frac{32}{16} \mathrm{~s}^{2-}\)
Note: Before using the notation ![]() find out whether the speclés is a neutral atom, acation or an anion, If it is a neutral atom, Atomic number (Z) = number of protons in the nucleus of an atom = number of electrons in a neutral atom is valid, i.e., number of protons = number of electrons = atomic number. If the species is an ion, determine whether the number of protons are larger (cation, positive ion) or smaller (anion, negative ion) than the number of electrons. Number of neutrons is always given by A-Z, whether the species is neutral or ion.
find out whether the speclés is a neutral atom, acation or an anion, If it is a neutral atom, Atomic number (Z) = number of protons in the nucleus of an atom = number of electrons in a neutral atom is valid, i.e., number of protons = number of electrons = atomic number. If the species is an ion, determine whether the number of protons are larger (cation, positive ion) or smaller (anion, negative ion) than the number of electrons. Number of neutrons is always given by A-Z, whether the species is neutral or ion.
Question 3.
The Vividh Bharati station of All India Radio, Delhi, broadcasts on a frequency of 1,368 kHz (kilo hertz). Calculate the wavelength of the electro-magnetic radiation emitted by transmitter. Which part of the electromagnetic specturm does it belong to?
Solution:
The wavelength, λ, is equal to c/v. where c is the speed of electromagnetic radiation in vacuum and v is the frequency. Substituting the given values, we have

Question 4.
The wavelength range of the visible spectrum extends from violet (400 nm) to red (750 nm). Express these wave
lengths in frequencies (Hz). (1 nm = 10-9 m).
Solution:
Using c = v λ frequency of violet light.
V = \(\frac{\mathrm{c}}{\mathrm{v}}=\frac{3.00 \times 10^8 \mathrm{~ms}^{-1}}{400 \times 10^{-9} \mathrm{~m}}\)
= 7.50 × 1014 Hz
Frequency of red light
v = \(\frac{c}{v}=\frac{3.00 \times 10^8 \mathrm{~ms}^{-1}}{750 \times 10^{-9} \mathrm{~m}}\) = 4.00 × 1014 Hz
The range of visible spectrum is from
4.0 × 1014 to 7.5 × 1014Hz in terms of frequency units.
Question 5.
Calculate
(a) wave number and
(b) frequency of yellow radiation having wavelength 5000 A.
Solution:
(a) Calculation of wavenumber \((\bar{v})\)
λ = 5800 A = 5800 × 10-8 cm
= 5800 × 10-10m
\((\bar{v})\) = \(\frac{1}{\lambda}=\frac{1}{5800 \times 10^{-10} \mathrm{~m}}\)
= 1.724 × 106m-1
= 1.724 × 104 cm-1
Question 6.
Calculate energy of one mole of photons of radiation whose frequency is 5 × 1014 Hz.
Solution:
Energy (E) of one photon is given by the expression
E = hv .
h = 6.626 × 10-34 J s
v = 5 × 1014 s-1 (given)
E = (6.626 × 10-34J s) × (5 × 1014 s-1)
= 3.313 × 10-19 J
Energy of one mole of photons
= (3.313 × 10-19J) × (6.022 × 1023 mol-1)
= 199.51 kJ mol-1.
Question 7.
A 100 watt bulb emits monochromatic light of wavelength 400 nm. Calculate the number of photons emitted per second by the bulb.
Solution:
Power of the bulb = 100 watt
= 100 J s-1
Energy of one photon E = hv = hc/λ.
= \(\frac{6.626 \times 10^{-34} \mathrm{Js} \times 3 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{400 \times 10^{-19} \mathrm{~m}}\)
= 4.969 × 10-19J
Number of photons emitted
\(\frac{100 \mathrm{~J} \mathrm{~s}^{-1}}{4.969 \times 10^{-19} \mathrm{~J}}\) = 2.012 × 1020 s-1
Question 8.
When electromagnetic radiation of wavelength 300 nm falls on the surface of sodium, electrons are emitted with a kinetic energy of 1.68 × 105 J mol-1. What is the minimum energy needed to remove an electron from sodium? What is the maximum wavelength that will cause a photoelectron to be emitted?
Solution:
The energy (E) of a 300 nm photon is given by
hv = hc/λ.
= \(\frac{6.626 \times 10^{-34} \mathrm{Js} \times 3.0 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{300 \times 10^{-9} \mathrm{~m}}\)
= 6.626 × 10-19 J
The energy of one mole of photons
= 6.626 × 10-19 J × 6.022 × 1023 mol-1
= 3.99 × 105 mol-1
The minimum energy needed to remove one mole of electrons from sodium
= (3.99 – 1.68) 105 J mol-1
= 2.31 × 105 J mol-1
The minimum energy for one electron
= \(\frac{2.31 \times 10^5 \mathrm{~J} \mathrm{~mol}^{-1}}{6.022 \times 10^{23} \text { elelctrons } \mathrm{mol}^{-1}}\)
= 3.84 × 10-19J
This corresponds to the wavelength
∴ λ = \(\frac{\mathrm{hc}}{\mathrm{E}}\)
= \(\frac{6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s} \times 3.0 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{3.84 \times 10^{-9} \mathrm{~J}}\)
= 517 nm
(This corresponds to green light)
Question 9.
The threshold frequency v0 for a metal is 7.0 × 1014 s-1. Calculate the kinetic energy of an electron emitted when radiation of frequency v = 1.0 × 1015 s-1 hits the metal.
Solution:
According to Einstein’s equation
Kinetic energy = 1/2 mev2 = h(v – v0)
= (6.626 × 10-34 J s)
(1.0 × 1015 s-1 – 7.0 × 1014 s-1)
= (6.626 × 10-34 J s)
(10.0 × 1014s-1 – 7.0 × 1014s-1)
= (6.626 × 10-34 J s)
(3.0 × 1014s-1) = 1.988 × 10-19 J
Question 10.
What are the frequency and wave-length of a photon emitted during a transition from n = 5 state to the n = 2 state in the hydrogen atom?
Solution:
Since n1 = 5 and nf = 2, this transition gives rise to a spectral line in the visible region of the Balmer series. From ΔE = \(\mathrm{R}_{\mathrm{H}}\left(\frac{1}{\mathrm{n}_i^2}-\frac{1}{\mathrm{n}_{\mathrm{f}}^2}\right)\)
= 2.18 × 10-18J\(\left(\frac{1}{n_i^2}-\frac{1}{n_f^2}\right)\)
ΔE = 2.18 × 10-18J\(\left(\frac{1}{5^2}-\frac{1}{2^2}\right)\)
= -4.58 × 10-19 J.
It is an emission energy.
The frequency of the photon (taking energy in terms of magnitude) is given by

Question 11.
Calculate the energy associated with the first orbit of He+. What is the radius this orbit?
Solution:
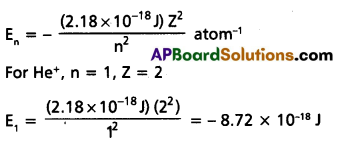
The radius of the orbit is given by
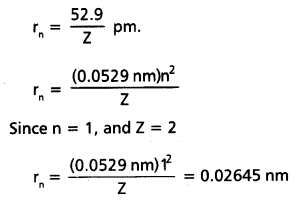
Question 12.
What will be the wavelength of a ball of mass 0.1 kg moving with a velocity of 10 m s-1?
Solution:
According to de Brogue λ = \(\frac{h}{m V}=\frac{h}{p}\)
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{\left(6.626 \times 10^{-34} \mathrm{Js}\right)}{(0.1 \mathrm{~kg})\left(10 \mathrm{~m} \mathrm{~s}^{-1}\right)}\)
= 6.626 × 10-34m (J = kg m2 s-2)
Question 13.
The mass of an electron is 9.1 × 10-31 kg. If its K.E. is 3.0 × 10-25 J, calculate its wavelength.
Solution:

Question 14.
Calculate the mass of a photon with wavelength 3.6 A.
Solution:
λ = 3.6 A = 36 × 10-10 m
Velocity of photon = velocity of light
m = \(\frac{\mathrm{h}}{\lambda v}=\frac{6.626 \times 10^{-34} \mathrm{Js}}{\left(3.6 \times 10^{-10} \mathrm{~m}\right)\left(3 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}\right)}\)
= 6.135 × 10-29kg
Question 15.
A microscope using suitable photons is employed to locate an electron in an atom within a distance of 0.1 A. What
is the uncertainty involved in the measurement of its velocity?
Solution:
∆x ∆p = \(\frac{h}{4 \pi}\) or ∆x m∆v = \(\frac{h}{4 \pi}\)
∆v = \(\frac{h}{4 \pi \Delta x m}\)
∆v = \(\frac{6.626 \times 10^{-34} \mathrm{Js}}{4 \times 3.14 \times 0.1 \times 10^{-10} \mathrm{~m} \times 9.1 \times 10^{31} \mathrm{kc}}\)
= 0.579 × 107 m s-1 (1 J = 1 kg m2 s-2)
= 5.79 × 106 ms-1
Question 16.
A golf ball has a mass of 40g and a speed of 45 m/s. If the speed can be measured within accuracy of 2%, calculate the uncertainty in the position.
Solution:
The uncertainty in the speed is 2%, i.e.,
4 × \(\frac{2}{100}\) = 0.9 ms-1
Using the λ = \(\frac{\mathrm{h}}{\mathrm{mv}}=\frac{\mathrm{h}}{\mathrm{p}}\)
Δx = \(\frac{h}{4 \pi m \Delta v}\)
= \(\frac{6.626 \times 10^{-34} \mathrm{Js}}{4 \times 3.14 \times 40 \mathrm{~g} \times 10^{-3} \mathrm{~kg} \mathrm{~g}^{-1}\left(0.9 \mathrm{~ms}^{-1}\right)}\)
= 1.46 × 10-33 m
This is nearly \(\sim\) 1018 times smaller than the diameter of a typical atomic nucleus. As mentioned earlier for large particles, the uncertainty principle sets no meaningful limit to the precision of measurements.
Question 17.
What is the total number of orbitals associated with the principal quantum number n = 3?
Solution:
For n = 3, the possible values of 1 are 0, 1 and 2. Thus there is one 3s orbital (n = 3, l = 0 and ml = 0); there are three 3p orbitals
(n = 3, 1 = 1 and ml = -1, 0, +1); there are five 3d orbitais (n = 3, l = 2 and ml = -2, -1, 0, +1, +2).
Therefore, the total number of orbitals is 1 + 3 + 5 = 9
The same value can also be obtained by using the relation; number of orbitals = n2,
i.e. 32 = 9
Question 18.
Using s, p, d, f notations, describe the orbital with the following quantum numbers
(a) n = 2, l = 1,
(b) n = 4, l = 0,
(c) n = 5, l = 3,
(d) n = 3, l = 2
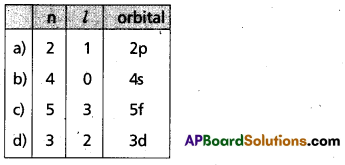
Solution:
Question 19.
Calculate its wave length of 1st line in Balmer series of hydrogen spectrum.
Solution:
Ryd berg’s equation \(\bar{v}\) = \(\frac{1}{\lambda}\) = \(\mathrm{R}_{\mathrm{H}}\left[\frac{1}{\mathrm{n}_1^2}-\frac{1}{\mathrm{n}_2^2}\right]\)
For the 1st line of Balmer series
n1 = 2, n2 = 3
R = 1,09,677 cm-1
\(\bar{v}\) = \(\frac{1}{\lambda}\) = 1,09,677\(\left[\frac{1}{2^2}-\frac{1}{3^2}\right]\)
= 1,09,677 × \(\frac{5}{36}\)
Wave no. \((\bar{v})\) = 15232.9 cm-1
Wave length λ = \(\frac{1}{\bar{v}}\) = \(\frac{1}{15232.9}\) = 6.5 × 10-5 cm-1
Question 20.
Calculate the shortest wave length in lyman series of hydrogen spectrum (RH = 1,09,677 cm-1).
Solution:
To calculate shortest wave length

Question 21.
What is the maximum no.of emission lines when the excited electron of a ‘H’ atom in n =6 drops to ground state.
Solution:
The no. of spectral lines found when an electron return from nth orbit to ground state.
= \(\frac{n(n-1)}{2}\) = \(\frac{6(6-1))}{2}\) = \(\frac{30}{2}\) = 15
Question 22.
Calculate the longest wavelength transition in the paschen series of He+.
Solution:

Question 23.
The no. of waves in the forth Bohr’s orbit of hydrogen is
a) 3
b) 4
c) 9
d) 12
Solution:

Question 24.
It the speed of the electron in 1st Bohr’s orbit of hydrogen is x, then the speed of the electron in the 3rd orbit of hydrogen is
Solution:
Given
Velocity of electron in 1st Bohr’s orbit of hydrogen = x
Velocity of electron in 3rd Bohr’s orbit of hydrogen = \(\frac{x}{n}\) = \(\frac{x}{3}\)
Question 25.
The ratio of radii of the fifth orbits of He+ and Li+2 will be
a) 2 : 3
b) 3 : 2
c) 4 : 1
d) 5 : 3
Solution:
Z2(li)=3
Z1 (He) = 2
\(\frac{r_1}{r_2}\) = \(\frac{Z_2}{Z_1}\) = \(\frac{3}{2}\) = 3 : 2
Question 26.
What is the lowest value of ‘n’ that allows ‘g’ orbitals to exist ?
Solution:
The lowest value of ‘n that allows ‘g’ orbitals to exist is ‘5’.
Question 27.
What is the orbital angular momentum of a d-electron
Solution:
Orbital angular momentum = \(\sqrt{l(l+1)} \frac{\mathrm{h}}{2 \pi}\)
For a d electron l = 2
= \(\sqrt{2(2+1)} \frac{h}{2 \lambda}\)
= \(\frac{\sqrt{6 h}}{2 \lambda}\)
Question 28.
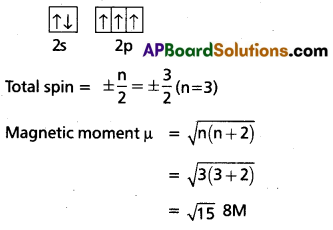
What is the total spin and magnetic moment of an atom with atomic number 7’?
Solution:
Z = 7 (Nitrogen)
Electronic configuration is 1s2 2s2 2p3 (in ground state)
Question 29.
The quantum number of electrons are given below. Arrange in order of increasing energies.

Solution:
a) 4d
b) 3d
c) 4p
d) 3d
e) 3p
f) 4p
∴ Increasing order of energy
e < b = d < c = f < a
Question 30.
If the value of n + l = 7 then what should be the increasing order of energy of the possible subshells.
Solution:
Given
n + l = 7
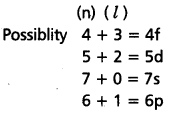
∴ The increasing order of energy
4f < 5d < 6p < 7s
(According Aufbau principle)
Question 31.
Which of the following sets of quantum number is not permitted?
a) n = 3, l = 3, m = +1, s = +\(\frac{1}{2}\)
b) n = 3, l = 3, m = +2, s = –\(\frac{1}{2}\)
c) n = 3, l = 1, m = +2, s = –\(\frac{1}{2}\)
d) n = 3, l = 0, m = 0, s = +\(\frac{1}{2}\)
Solution:
Only d is permitted i.e., 3s1
In a, b n = l but n always > l
in c m = + 2 is not permitted
Because l = 1,’m’ has -1, 0, +1 values only.
Question 32.
Ground state electronic configuration of nitrogenators can be represented as

Solution:
(a) and (d) are correct representations.
Question 33.
Which of the following is possible
a) 3f
b) 4d
c) 2d
d) 3p
Solution:
4d and 3p are possible.