AP State Syllabus AP Board 9th Class Physical Science Solutions Chapter 1 Motion Textbook Questions and Answers.
AP State Syllabus 9th Class Physical Science Solutions 1st Lesson Motion
9th Class Physical Science 1st Lesson Motion Textbook Questions and Answers
Improve Your Learning
Question 1.
As shown in following figure, a point traverses the curved path.
Draw the displacement vector from given points A to B.

Answer:

As the point traverses from A to B, the displacement is the shortest distance between A and B. Hence the displacement vector will be as follows.
Question 2.
“She moves at a constant speed in a constant direction.” Rephrase the same sentence in fewer words using concepts related to motion. (AS 1)
Answer:
“She moves with constant velocity”.
Reason :
Constant speed in a constant direction is nothing but ‘constant velocity’.
Question 3.
What is the average speed of a Cheetah that sprints 100 m in 4 sec? What if it sprints 50 m in 2 sec? (AS 1, AS7)
Answer:

Question 4.
Correct your friend who says, “The car rounded the curve at a constant velocity of 70 km/h”. (AS 1)
Answer:
“The car rounded the curve at a constant speed of 70 km/h”.
![]()
Reason :
In a circular motion, speed remains constant but velocity changes.
Question 5.
Suppose that the three balls shown in figure below start simultaneously from the top of the hills. Which one reaches the bottom first? Explain.
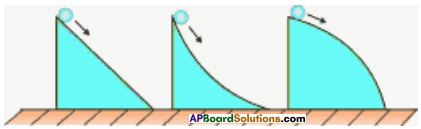
Answer:
Ball from first hill reaches the bottom first.
Reason :
- In the first hill, the ball has uniform rectilinear motion.
- So, the speed and velocity have same magnitude and direction.
- In the second and third hills, the ball takes curved path.
- So, the direction of velocity changes.
Question 6.
In the figure given below distance vs time graphs showing motion of two cars A and B are given. Which car moves fast? (AS 1)
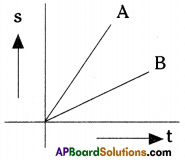
Answer:
Car A moves fast.
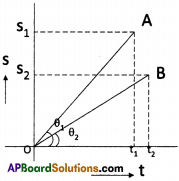
Reason :
- If we draw perpendiculars to X and Y axes from A and B respectively, we can observe that A covers large distance (S1) within a short time (t1).
- Find the slopes of the lines OA and OB at any instant. Slope of OA is high. Hence car A moves faster.
Question 7.
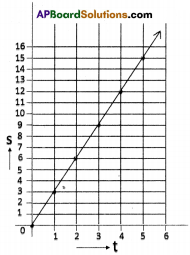
Draw the distance vs time graph when the speed of a body increases uniformly. (AS 5)
Answer:
Let us consider a car moves as shown in the table.
| Time (t) sec | Distance in meters |
| 0 sec | 0 meters |
| 1 sec | 3 meters |
| 2 sec | 6 meters |
| 3 sec | 9 meters |
| 4 sec | 12 meters |
| 5 sec | 15 meters |
Now draw a s-t graph.
Question 8.
Draw the distance-time graph when its speed decreases uniformly. (AS 5)
Answer:
Let us consider the movement of a car after applying brakes.
| Time (t) sec | Distance in meters |
| 0 sec | 20 meters |
| 1 sec | 18 meters |
| 2 sec | 16 meters |
| 3 sec | 14 meters |
| 4 sec | 12 meters |
| 5 sec | 10 meters |
Now draw distance-time graph.

Question 9.
A car travels at a speed of 80 km/h during the first half of its running time and at 40 km/h during the other half. Find the average speed of the car. (AS 1, AS 7)
Answer:
Let the total running time = x hrs

Question 10.
A car covers half the distance at a speed of 50 km/h and the other half at 40 km/h. Find the average speed of the car. (AS 1, AS 7)
Answer:
Let the total distance = x km.
First half is covered with a speed of 50 km/h.

Question 11.
Derive the equation for uniform accelerated motion for the displacement covered in its nth second of its motion. (sn = u + a ( n – \(\frac{1}{2}\)) (AS 1)
Answer:
We know that distance travelled by an object in t seconds Is s = ut + \(\frac{1}{2}\) at²
∴ Distance travelled in ‘n’ seconds, s(n sec) = un + \(\frac{1}{2}\)an² ………. (1)
Distance travelled in (n – 1) seconds, s(n – 1) = u(n – 1) + \(\frac{1}{2}\) a(n – 1)² …….. (2)
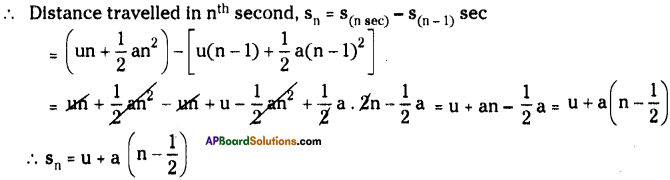
Question 12.
A particle covers 10m in first 5 sec and 10m in next 3 sec. Assuming constant acceleration. Find initial speed, acceleration and distance covered in next 2 sec. (AS 1, AS 7)
Answer:
Distance covered in first 5 sec = 10

To find the distance covered in next 2 sec, we have to find the initial speed after 8 sec
i.e., the final velocity after 8 sec.

Question 13.
A car starts from rest and travels with uniform acceleration ‘α’, for some time and then with uniform retardation ‘β’ and comes to rest. The time of motion is “t”. Find the maximum velocity attained by it. (αβt/(α+β)) (AS 1, AS 7)
Answer:
Acceleration a = a m/sec²
Initial speed u = 0 m/sec
Let the time be t1 sec.
From equation v = u + at
⇒ v = 0 + αt1
\(\therefore \mathrm{t}_{1}=\frac{\mathrm{v}}{\alpha} \mathrm{sec}\)
Retardation a = – β m/sec²
Initial speed ‘u’ is equal to the final
velocity with acceleration ‘α’
= u = αt1 m/sec
Final velocity v = 0 m/sec
Let the time be t2 sec

Question 14.
A man is 48m behind a bus which is at rest. The bus starts accelerating at the rate of 1 m/s², at the same time the man starts running with uniform velocity of 10 m/s. What is the minimum time in which the man catches the bus? (AS 1, AS 7)
Answer:
Bus is at rest.
∴ u = 0; a = 1 m/sec²
Let the bus cover the distance ‘s’ in ‘n’ seconds.
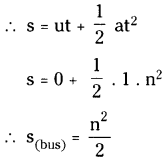
A man running with uniform velocity, v = 10 m/sec.
Distance covered by man in n seconds = 10 nm.
But after ‘n’ seconds the man catches the bus.
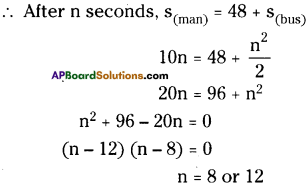
∴ The minimum time in which the man catches the bus is 8 sec.
Question 15.
A body leaving a certain point “O” moves with a constant acceleration. At the end of the fifth second, its velocity is 1.5 m/s. At the end of the sixth second, the body stops and then begins to move backwards. Find the distance traversed by the body before it stops. Determine the velocity with which the body returns to point “0”. (AS 1)
Answer:
Velocity in 5th sec = 1.5 m/sec ; The body comes to rest in 6th sec.
∴ Final velocity in 6th sec, v = 0
∴ Acceleration in 6th sec is v = u + at ⇒ 0 = 1.5 + a. 1 ⇒ a = -1.5 m/sec²
[The velocity in 5th sec becomes the initial velocity for 6th sec]
After 6 sec, the body comes to rest.
∴ v = 0, a = -1.5 m/sec², u = ?, t = 6 sec.
v = u + at ⇒ 0 = u – 1.5 × 6 ⇒ u = 9 m/sec.
∴ Distance traversed by the body in 6 sec. i.e., before it stops.
s = ut + \(\frac{1}{2}\) at² = 9 × 6 + \(\frac{1}{2}\) × – 1.5 × 6² = 54 – 27 = 27m.
For backward journey,
u = 0 m/sec, t = 6 sec, a = -1.5 m/sec²
v = u + at ⇒ v = 0 – 1.5 × 6 ⇒ v = – 9
∴ Velocity for backward journey is – 9 m/sec.
![]()
Question 16.
Distinguish between speed and velocity.(AS 1)
Answer:
| Speed | Velocity |
| 1. The distance covered in unit time is called average speed. | 1. The displacement of an object per unit time is called average velocity. |
| 2. Speed = \(\frac{\text { Distance }}{\text { Time }}\) | 2. Velocity =\(\frac{\text { Displacement }}{\text { Time }}\) |
| 3. Speed is scalar. | 3. Velocity is vector. |
| 4. Speed gives the idea of how fast the body moves. | 4. Velocity gives the idea of how fast the body moves in specified direction. |
Question 17.
What do you mean by constant acceleration? ((AS 1)
Answer:
- Acceleration is the rate of change of velocity.
2 - It gives an idea how quickly velocity of a body is changing.
- Acceleration is uniform, when in equal intervals of time, equal changes of velocity occurs.
- For example, while driving a car, if we steadily increase the velocity from 30 km/h to 35 km/h in 1 sec and 35 km/h to 40 km/h in the next second and so on. In this case the acceleration is 5km/h, is said to be constant acceleration.
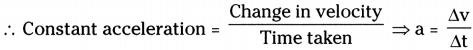
Question 18.
When the velocity is constant, can the average velocity over any time interval differ from instantaneous velocity at any instant ? If so, give an example; if not, explain why. (AS 2, AS 1)
Answer:
No. Here velocity is constant.
∴ Average velocity over any time interval is same and the instantaneous velocity at any instant is same.
Ex : Let us consider a car moves on a straight road with constant velocity say 10 m/s.
1) Now let the distance covered (AB) by the car in 1 s = 10 m.
![]()
2) Distance covered in 2s (AC) = 20 m.
Average velocity from A to C is \(\frac{20 m}{2 s}\) = 10 m/s.
3) Instantaneous velocity at A or B or C at any point = 10 m/s.
![]()
Question 19.
Can the direction of velocity of an object reverse when its acceleration is constant? If so give an example; if not, explain why? (AS 2, AS 1)
Answer:
Yes. In case of a vertically projected body, while the body is moving up, the direction of velocity is upward, whereas while it is falling down, the direction of velocity is downward. Acceleration in both the cases is constant (numerically).
Question 20.
A point mass starts moving in a straight line with constant acceleration V’. At a time t after the beginning of motion, the acceleration changes sign, without change in magnitude. Determine the time t0 from the beginning of the motion in which the point mass returns to the initial position. (AS 1)
Answer:


Question 21.
Consider a train which can accelerate with an acceleration of 20 cm/s² and slow down with deceleration of 100 cm/s². Find the minimum time for the train to travel between the stations 2.7 km apart. (AS 1)
Answer:
Let the Acceleration of the train a = 20 cm/s²
Deceleration of the train β = 100 cm/s²
Distance between the two stations s = 2.7 km = 27 × 104 cm
Let the minimum time for the train to travel between the two stations is t sec.

Question 22.
You may have heard the story of the race between the rabbit and tortoise. They started from same point simultaneously with constant speeds. During the journey, rabbit took rest somewhere along the way for a while. But the tortoise moved steadily with lesser speed and reached the finishing point before rabbit. Rabbit woke up and ran, but rabbit realized that the tortoise had won the race. Draw distance vs time graph for this story. (AS 5)
Answer:
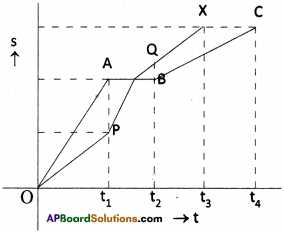
- OX – movement of tortoise.
- OABC – movement of rabbit
- Rabbit and tortoise start at O’.
- After time tj rabbit is at A and tortoise is at P.
- Rabbit takes rest up to time t2.
- After time t2, tortoise is at Q, but rabbit has no displacement.
- After time t3, the tortoise reaches the destination ‘X’.
- But rabbit reaches the destination after time t4.
Question 23.
A train of length 50 m is moving with a constant speed of 10 m/s. Calculate the time taken by the train to cross an electric pole and a bridge of length 250 m. (AS 1)
Answer:
Length of the train 50 m.; Speed of the train v = 10 m/s.
Distance travelled while crossing an electric pole = Length of the train = s = 50 m.
∴ Time taken to cross the electric pole ‘t’ = \(\frac{s}{v} \Rightarrow t=\frac{50}{10}\) = 5 s.
Length of the bridge = 250 m.
Distance travelled while crossing the bridge = Length of train + Length of bridge
= 50 + 250 = 300 m.
∴ Time taken to cross the bridge = \(\frac{300 \mathrm{~m}}{10 \mathrm{~m} / \mathrm{s}}\) = 30 sec.
![]()
Question 24.
Two trains each of having a speed of 30 km/h are headed at each other in opposite direction on the same track. A bird flies off one train to another with a constant speed of 60 km/h when they are 60 km apart till before they crash. Find the distance covered by the bird and how many trips the bird can make from one train to the other before they crash. (AS 1)
Answer:
Speed of each train = 30 km/hr
Speed of the bird = 60 km/hr
Distance between the two trains = 60 km
These two trains crash in one hour.
The bird flies a distance of 60 km till before the two trains crash.
The bird can make number of trips (infinity) before they crash.
Question 25.
A Stone dropped from top of a well reaches the surface of water in 2 seconds, find the velocity of stone while it touches the surface of water and what is the depth of the water surface from top of well (g=10m/s²) (Using V = U + at, S = Ut + 1/2 at²)
Answer:
Given that
t = 2s
u = 0 m/s [∵ free fall body]
v = ?
Depth s = ?
a = g = 10 m/s²
i) v = u + at
v = 0 + 10 × 2 = 20 m/s
ii) s = ut + – \(\frac{1}{2}\)at²
= 0 + \(\frac{1}{2}\) × 10 × 2²
= \(\frac{1}{2}\) × 10 × 4
= 20 m
Hence, velocity of stone while it touches the surface of water = 20 m/s
Depth of the water surface from the top of well = 20 m.
![]()
Question 26.
An object moving with 6m per second execute an acceleration 2 m/s² in next 3 seconds. How much distance it covered? (s = ut + 1/2 at²)
Answer:
u = 6 m/s; t = 3 sec; a = 2 m/s²
s = ut + \(\frac{1}{2}\) at²
= 6 × 3 + \(\frac{1}{2}\) × 2 × 3² = 18 + 9 = 27 m
The object covers 27 m in 3 sec.
Question 27.
A car stopped after travelling distance 8 m due to applying brakes at the speed of 40 m/s. Find acceleration and retardation of car in that period, (v² – u² = 2as)
Answer:
Here u = 40 m/s; v = 0 (vehical stopped); s = 8 m; a =?
v² – u² = 2as 0 – 40² = 2 × a × 8
a = \(\frac{-(40)(40)}{2 \times 8}\) =-100m/s
Acceleration = 100 m/s² with retordation on (-sign).
9th Class Physical Science 1st Lesson Motion InText Questions and Answers
9th Class Physical Science Textbook Page No. 1
Question 1.
If earth is in motion, why don’t we directly perceive the motion of the earth?
Answer:
Earth is in motion. We, the people on the earth also move with a speed equal to that of the earth. We cannot directly perceive the motion of the earth, because of this.
Question 2.
Are the walls of your classroom at rest or in motion? Why?
Answer:
The walls are at rest in view of our observation. When we discuss this in view of the motion of the earth, the walls are also in motion.
![]()
Question 3.
Have you ever experienced that the train in which you sit appears to move when it is at rest? Why?
Answer:
This happens when we sit in a stationary train and, the train on another track starts moving.
9th Class Physical Science Textbook Page No. 2
Question 4.
Why do we observe these changes?
Answer:
These changes are due to the point of observation. We know that earth is a sphere, the upward direction of the vertical position on its surface decisively depends upon the place on the earth’s surface, where the vertical is drawn.
Question 5.
Are the terms relative or not?
Answer:
The terms “longer”, “shorter”; “up” and “down”, etc. are relative to each other.
9th Class Physical Science Textbook Page No. 4
Question 6.
What answer may the passenger give to the driver?
Answer:
The car is in motion with respect to the observer on the road, but at rest with respect to the passenger. Because motion is a combined property of the observer and the body which is being observed.
Question 7.
How do we understand motion?
Answer:
A body is said to be in motion when its position is changing continuously with time relative to an observer.
9th Class Physical Science Textbook Page No. 6
Question 8.
Can you measure the average speed and average velocity?
Answer:
Yes, we can measure the average speed and average velocity.
![]()
Question 9.
How can you differentiate speed and average velocity?
Answer:
- Speed gives the idea of how fast the body moves.
- Velocity is the speed of an object in a specified direction.
9th Class Physical Science Textbook Page No. 7
Question 10.
Can you find the speed of the car at a particular instant of time?
Answer:
Yes, we can find the speed of the car at any instant of time by looking at its speedometer
Question 11.
What is the speed of the car at the instant of time ‘t3‘ for given motion?
Answer:
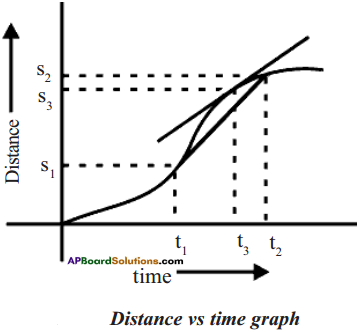
The instantaneous speed is represented by the slope of the curve at a given instant of time. We can find the slope of the curve at any point on it by drawing a tangent to the curve at that point. The slope of the curve gives speed of the car at that instant.
9th Class Physical Science Textbook Page No. 8
Question 12.
In what direction does an object move? Distance vs time graph
Answer:
The object moves in the direction tangential to the direction of the motion of the string.
![]()
Question 13.
Which motion is called uniform? Why?
Answer:
The motion of the body is said to be in uniform when its velocity is constant.
9th Class Physical Science Textbook Page No. 9
Question 14.
What is the shape of the graph?
Answer:
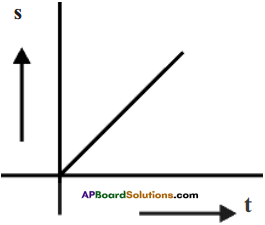
The shape of the graph for a body which is in uniform motion is a straight line as shown in the figure.
9th Class Physical Science Textbook Page No. 10
Question 15.
a) What is the shape of the graph?
Answer:
It is a curve.
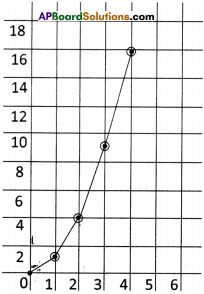
b) Is it a straight line or not? Why?
Answer:
The graph is not a straight line because the speed is changing irregularly.
Question 16.
Draw velocity vectors in the given figure at times t = 0, 1s, 2s, 3s.
Answer:
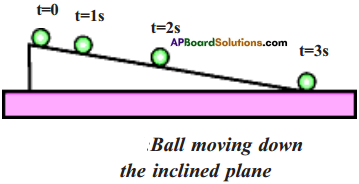
From the graph, we conclude that when the ball moves down the inclined plane its speed increases gradually but its direction remains constant.
9th Class Physical Science Textbook Page No. 11
Question 17.
Draw velocity vectors at times t = 1s, 2s, 3s in the given figure.
Answer:
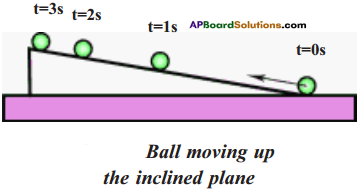
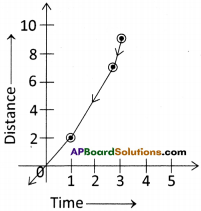
From the graph, we conclude that when the ball moves up the inclined plane its speed decreases gradually, but the direction of motion remains constant.
Question 18.
Can you give few examples for motion of an object where its speed remains constant but velocity changes?
Answer:
For the bodies which are in uniform in circular motion the speed remain constant but velocity change. Ex : Rotation of earth, revolution of moon around the earth, etc.
Question 19.
Is the direction of motion constant? How?
Answer:
No, the direction of motion also changes continuously.
![]()
Question 20.
Can you give some more examples where speed and direction simultaneously change?
Answer:
Motion of a rocket, horizontally projected body, kicked football, a cricket ball bowled by a bowler, etc.
9th Class Physical Science Textbook Page No. 12
Question 21.
What is acceleration? How can we know that a body is accelerating?
Answer:
- Acceleration gives an idea how quickly velocity of a body changing.
- It is equal to the rate of change in velocity.
- While travelling in a bus or car, when the driver presses the accelerator, the passen¬gers sitting in the bus experience acceleration. Their bodies press against the seats due to acceleration.
Question 22.
At which point is the speed maximum?
Answer:
At B, the speed will be maximum.
Question 23.
Does the object in motion possess acceleration or not?
Answer:
Any object which is in motion possesses acceleration.
9th Class Physical Science Textbook Page No. 5
Question 24.
What is the displacement of the body if it returns to the same point from where it started? Give one example from daily life.
Answer:
When a body returns to the same point where it is started, then the displacement is zero.
Ex: A man starts from his home, goes to a market and returns home. Then his displacement is zero.
![]()
Question 25.
When do the distance and magnitude of displacement become equal?
Answer:
The distance and the magnitude of displacement become equal when the body moves along a straight line in one direction.
9th Class Physical Science Textbook Page No. 6
Question 26.
What is the average speed of the car if it covers 200 km in 5 h?
Answer:
Distance = 200 km ; Time = 5 h
![]()
Question 27.
When does the average velocity become zero?
Answer:
The average velocity of a body becomes zero when its displacement is zero.
Question 28.
A man used his car. The initial and final odometer readings are 4849 and 5549 respectively. The journey time is 25h. What is his average speed during the journey?
Answer:
Distance covered = 5549 – 4849 = 700 km.
Time = 25h.
![]()
9th Class Physical Science Textbook Page No. 9
Question 29.
Very often you must have seen traffic police stopping motorists or scooter drivers who drive fast and fine them. Does fine for speeding depend on average speed or instantaneous speed? Explain.
Answer:
Instantaneous speed.
![]()
Question 30.
One airplane travels due north at 300 km/h and another airplane travels due south at 300 km/h. Are their speeds the same? Are their velocities the same? Explain.
Answer:

- Speed is same.
- Velocities are same in magnitude but differs in direction in the observer’s point of view.
Question 31.
The speedometer of the car indicates a constant reading. Is the car in uniform motion? Explain.
Answer:
Yes.
- The indicator in speedometer changes its position even for a small change in speed.
- As it indicates a constant reading, the car moves equal distances at equal intervals of time.
- Hence the motion is uniform.
9th Class Physical Science Textbook Page No. 11
Question 32.
An ant is moving on the surface of a ball. Does it’s velocity change or not? Explain.
Answer:
Velocity changes.
As the ant is moving on the surface of a ball, it has to go in circular motion.
![]()
Question 33.
Give an example of motion where there is a change only in speed but no change in direction of motion.
Answer:
Motion of a bus on the road.
9th Class Physical Science Textbook Page No. 13
Question 34.
What is the acceleration of a race car that moves at constant velocity of 300 km/h?
Answer:
Velocity = 300 km/h = \(300 \times \frac{5}{18}=\frac{500}{6}\) = 83.33 m/sec
As the velocity is constant, the acceleration is also constant.
∴ Acceleration = 83.33 m/sec².
Question 35.
Which has the greater acceleration, an airplane, that goes from 1000 km/h to 1005 km/h in 10s or a skateboard that goes from zero to 5km/h in 1 second?
Answer:

Question 36.
What is the deceleration of a vehicle moving in a straight line that changes its velocity from 100 km/h to a dead stop in 10 sec?
Answer:

Question 37.
Correct your Mend who says “Acceleration gives an idea of how fast the position changes.”
Answer:
“Acceleration gives the idea of how fast the position changes in a given direction.”
9th Class Physical Science 1st Lesson Heat Activities
Activity 1 Distance and Displacement
Question 1.
Draw a graph showing the difference between distance and displacement.
Answer:
- Take a ball and throw it into the air with some angle to the horizontal.
- Observe its path and draw it on paper.
- The figure shows the path taken by the ball.
- The distance ASB gives the distance travelled by the ball.
- The length of \(\overrightarrow{\mathrm{AB}}\) gives the displacement of the ball.
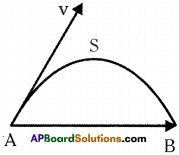
Displacement:
Displacement is the shortest distance between initial and final points in a specified direction represented by a vector.
Distance :
Distance is the length of the path traversed by an object in a given time interval.
Activitie – 2 Drawing displacement vectors
Question 2.
Draw displacement vectors from A to B in the following situations.
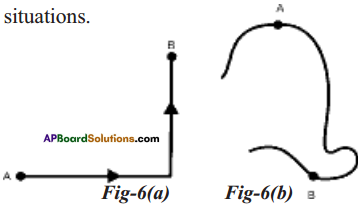
Answer:
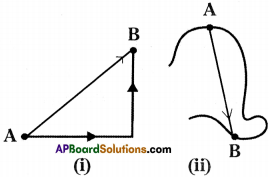
Activitie – 3 Measuring the average speed
Question 3.
How can the average speed be measured?
Answer:
- Select two positions (say A and B) 50 meters apart in the ground.
- Ask some students to stand at point A.
- Ask another group of students with stop watches to stand at B.
- When you clap your hand, the students at A start running towards the point B in any direction or path.
- At the same time the students at B start their stop watches.
- Observe that for each runner there is a student at B to measure the time taken for completing the race.
- Note the time taken by each student to cover the distance between the points A and B in the table given below.
Student Time taken to reach B (Sec.) Average speed (50 ft) m/s A1 t1 ……… A2 t2 ……… A3 t3 ……… - The student who took the least time to reach B (from A) is said to be the fastest runner.
- The student who is fastest runner has the greatest average speed.
- Thus we measure the average speed of any moving body.
Activity – 4 Observing the direction of motion of a body
Question 4.
Show that the direction of velocity is tangent to the path at a point of interest when a body is in uniform circular motion.
Answer:
- Carefully whirl a small object on the end of the string in the horizontal plane.
- Release the object while it is whirling on the string.
- We observe that the body along the tangent at the point where we released the body.
- Try to release the object at different points on the circle and observe the direction of motion of object after it has been released form the string.
- We will notice that the object moves on a straight line along the tangent to the circle at the point where we released it.
Activity – 5 Understanding uniform motion
Question 5.
Describe uniform motion.
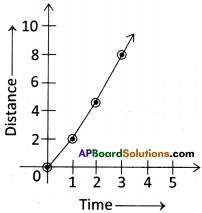
Answer:
1) Consider a cyclist moving on a straight road.
2) The distance covered by him with respect to time is given in the following table.
| Time (t in seconds) | Distance (s in meters) |
| 0 | 0 |
| 1 | 4 |
| 2 | 8 |
| 3 | 12 |
| 4 | 16 |
| – | – |
3) Draw distance vs time graph for the given values in the table.
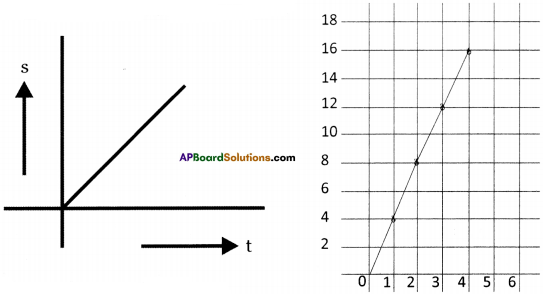
4) The graph will be as shown in the figure.
5) The straight line graph shows that the cyclist covers equal distances in equal inter¬vals of time.
6) If the direction of motion of the cyclist is assumed as constant, then we conclude that velocity is constant.
7) The motion of the body is said to be uniform when its velocity is constant.
Activity – 6 Observing the motion of a ball on an inclined plane
Question 6.
Describe an activity to explain the situation that “the speed changes but the direction of motion remains constant”.
Answer:
1) Set up an inclined plane as shown in the figure.
2) Take a ball and release it from the top of the inclined plane.
3) The positions of the ball at various times are shown in the figure given below.

4) On close observation we find that when the ball moves down on the inclined plane, its speed increases gradually, and the direction of motion remains constant on inclined plane.
5) Now push the ball till it acquires certain speed and release it with that speed from the bottom of the inclined plane.

6) We observe that the ball moves upward to a certain distance and comes back to the bottom.
7) From this we conclude that the speed changes but the direction of motion remains constant.
Activity – 7 Observing uniform circular motion
Question 7.
Explain with an example where “speed remains constant, but its velocity changes”.
Answer:
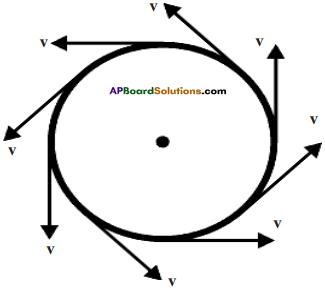
- Whirl continuously a stone which is tied to the end of the string.
- Draw its path of motion and velocity vectors at different positions as shown in figure.
- Assume that the speed of stone is constant.
- We observe that the path of the stone is a circle, and the direction of velocity changes at every instant of time, but the speed is constant.
- In this activity, we observe that though speed remains constant, its velocity changes.
Activity – 8 Observing the motion of an object thrown into air
Question 8.
Explain an activity to observe where speed and direction of motion change continuously.
Answer:
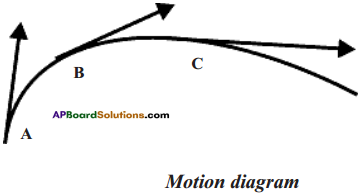
- Throw a stone into the air by making some angle with the horizontal.
- The path of the stone and velocity vectors are as shown in the figure.
- Here we observe that the speed of stone is not uniform as it traverses different distances at different intervals of time and finally comes to rest.
- The direction of motion is also not constant, as shown by the velocity vectors.
- In this activity, we noticed that the speed and direc¬tion of motion both change continuously.
Lab Activity
Question 9.
Describe an activity to find the acceleration and velocity of an object moving on inclined track.
Answer:
Aim : To find the acceleration and velocity of an object moving on an inclined track. Materials required: Glass marbles, book, digital clock, long plastic tubes and steel plate.
Procedure:
- Take a long plastic U type flat electrical wire cassing channel of length nearly 200 cm. Use this channel as track.
- Mark the readings in cm, along the track.
- Place one end of the track on a book and the other end on the floor.
- Keep a steel plate on the floor at the bottom of the track.
- Consider the reading at the bottom of the track as zero.
- Take a marble having enough size to travel in the track freely.
- Now release the marble freely from a certain distance say 40 cm.
- Start the digital clock when the marble is released.
- It moves down on the track and strikes the steel plate.
- Stop the digital clock when a sound is produced.
- Repeat the same experiment for the same distance 2 to 3 times and note the values of times in the table.

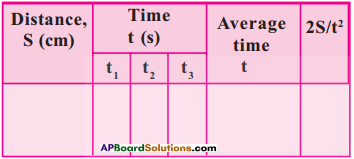
- Repeat the same experiment or various distances.
- Draw s -1 graph for above values.
- Do the above experiment by various slopes of the track and find acceleration in each case.
Conclusions :
- As the slope increases, acceleration increases.
- When iron block is used, we obtain the same conclusion as above. (The numerical values are less than the numerical values when marble is used)