AP SCERT 9th Class Maths Textbook Solutions Chapter 8 చతుర్భుజాలు InText Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 8th Lesson చతుర్భుజాలు InText Questions
ప్రయత్నించండి
1. AB ని E వరకు పొడిగించండి. \(\angle \mathrm{CBE}\) ని కనుగొనండి. మీరు ఏమి గమనించారు ? \(\angle \mathrm{ABC}\) మరియు \(\angle \mathrm{CBE}\) లు ఎటువంటి కోణాలు ? (పేజీ నెం. 177)
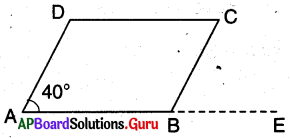
సాధన.
ABCD ఒక సమాంతర చతుర్భుజము మరియు
\(\angle \mathrm{A}\) = 40°
∴ ABC = 180° – 409
= 140 CBE = 40° (: A మరియు CBE లు
సదృశ కోణాలు) మరియు 2CBE మరియు LABC లు రేఖీయద్వయాలు.
![]()
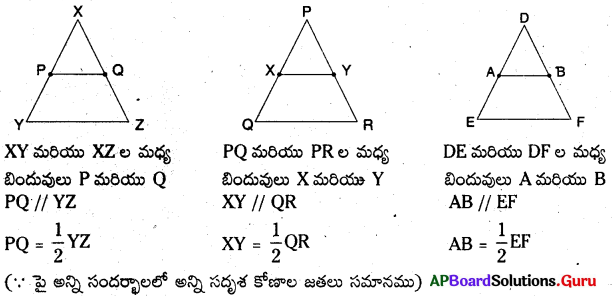
2. ∆ABC త్రిభుజం గీయండి. \(\overline{\mathrm{AB}}\) మరియు \(\overline{\mathrm{AC}}\) మధ్య బిందువులుగా E మరియు F లుగా గుర్తించండి. E, F లను పటంలో చూపిన విధంగా కలపండి. త్రిభుజంలో EF కొలతను, మూడవ భుజం BC కొలతను కొలవండి. అదే విధంగా \(\angle \mathrm{AEF}\) మరియు \(\angle \mathrm{ABC}\) కోణాలను కలపండి.
మనకు \(\angle \mathrm{AEF}=\angle \mathrm{ABC}\) మరియు \(\overline{\mathrm{EF}}\) = \(\frac {1}{2}\) \(\overline{\mathrm{BC}}\) అని వస్తుంది.
ఈ కోణాలు EF, BC రేఖలపై తిర్యగ్రేఖ AB తో ఏర్పడిన సదృశకోణాలు కావున మనం EF//BC అని చెప్పవచ్చు. మరికొన్ని త్రిభుజాలు గీచి, ఫలితాలను సరిచూడండి. (పేజీ నెం. 188)
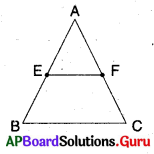
సాధన.
ఆలోచించి, చర్చించి రాయండి
1. చతురస్రంలో కర్ణాలు సమానమని, అవి పరస్పరం లంబ సమద్విఖందన చేసుకుంటాయని చూపండి. (పేజీ నెం. 185)
సాధన.
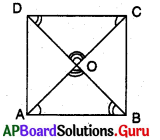
ABCD ఒక చతురస్రము అనుకొనుము.
AB = BC = CD = DA అగును.
∆ABC మరియు ∆BAD లలో
AB = AB (ఉమ్మడి భూమి)
\(\angle \mathrm{B} = \angle \mathrm{A}\) (ప్రతికోణం 90°)
BC = AD (సమాన భుజాలు)
∴ ∆ABC ≅ ∆BAD (భు.కో. భు నియమము నుండి)
⇒ AC = BD (CPCT)
అదే విధముగా ∆AOB మరియు ∆COD లలో
\(\angle \mathrm{OAB}=\angle \mathrm{OCD}\) [∵ ఏకాంతర కోణాలు]
\(\angle \mathrm{OBA}=\angle \mathrm{ODC}\) [∵ ఏకాంతర కోణాలు]
AB = DC (చతురస్ర భుజాలు)
∴ ∆AOB ≅ ∆COD (కో.భు. కో, నియమం)
కావున AO = OC (CPCT) ⇒ AC మధ్య బిందువు O
BO = OD (CPCT) ⇒ BD మధ్య బిందువు O
∴ AC మరియు BDల మధ్య బిందువు O.
∴ కర్ణాలు సమద్విఖండన చేసుకొనును.
∆AOB మరియు ∆COB లలో
AB = BC (దత్తాంశము)
OB = OB (ఉమ్మడి భుజము)
AO = OC (నిరూపించబడినది)
∴ ∆AOB ≅ ∆COB
(భు. భు, భు. నియమం ప్రకారం)
⇒ \(\angle \mathrm{AOB}=\angle \mathrm{COB}\) (CPCT)
కాని \(\angle \mathrm{AOB}=\angle \mathrm{COB}\) = 180° (∵ రేఖీయద్వయము)
∴ \(\angle \mathrm{AOB}=\angle \mathrm{COB}\) = \(\frac {180°}{2}\) = 90°
అదే విధముగా \(\angle \mathrm{AOB}=\angle \mathrm{COD}\) (∵ శీర్షాభిముఖ కోణాలు)
\(\angle \mathrm{BOC}=\angle \mathrm{AOD}\)
(∵ శీర్షాభిముఖ కోణాలు)
∴ AC ⊥ BD
చతురస్రంలోని కర్ణాలు లంబసమద్విఖండన చేసుకొనును.
![]()
2. రాంబలో కర్ణాలు దానిని నాలుగు సర్వసమాన త్రిభుజాలుగా విభజిస్తాయని చూపండి. (పేజీ నెం. 185)
సాధన.
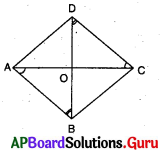
ABCD ఒక రాంబస్
AC మరియు BD లు ‘O’ బిందువు వద్ద ఖండించ
∆AOB మరియు ∆COD లలో
\(\angle \mathrm{OAB}=\angle \mathrm{OCD}\) (ఏకాంతర కోణాలు)
AB = CD (రాంబస్ నిర్వచనం)
\(\angle \mathrm{OBA}=\angle \mathrm{ODC}\) (ఏకాంతర కోణాలు)
∴ ∆AOB ≅ ∆COD ……. (1) (కో.భు. కో. నియమం ద్వారా)
⇒ AO = OC (CPCT)
అదే విధముగా ∆AOD ≅ ∆COD ……… (2) [∵ AO = OC; AD = CD; OD = OD భు.భు. భు. నియమం ప్రకారం]
ఇదే విధముగా ∆AOD ≅ ∆COB ……….. (3) అని నిరూపించవచ్చును.
(1), (2) మరియు (3) ల గుండి,
∆AOB ≅ ∆BOC ≅ ∆COD ≅ ∆AOD
∴ రాంబస్ యొక్క కర్ణాలు దానిని నాలుగు సర్వసమాన త్రిభుజాలుగా విభజిస్తాయి.
ఇవి చేయండి
ఒక సమాంతర చతుర్భుజాకారంలో కాగితాన్ని కత్తిరించండి. దాని కర్ణం వెంబడి మరలా కత్తిరించండి. ఎటువంటి ఆకారాలు ఏర్పడ్డాయి ? ఈ రెండు త్రిభుజాలను గూర్చి మీరు ఏమి చెబుతారు ? (పేజీ నెం. 179)
సాధన.
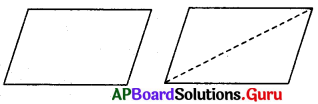
కాగితాన్ని కర్ణం వెంబడి కత్తిరించగా రెండు సర్వసమాన త్రిభుజాలు ఏర్పడ్డాయి.
సిద్ధాంతాలు
1. సమాంతర చతుర్భుజమును కర్ణము రెండు సర్వసమాన త్రిభుజాలుగా విభజిస్తుంది. (పేజీ నెం. 179)
సాధన.
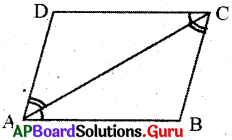
ABCD సమాంతర చతుర్భుజంను తీసుకోండి.
A, C లను కలపండి. సమాంతర చతుర్భుజానికి AC కర్ణం అవుతుంది.
AB || DC మరియు తిర్యగ్రేఖ కావున
\(\angle \mathrm{DCA}=\angle \mathrm{CAB}\) (ఏకాంతర కోణాలు)
ఇదే విధంగా DA || CB మరియు AC తిర్యగ్రేఖ.
కావున \(\angle \mathrm{DAC}=\angle \mathrm{BCA}\) అయినది.
ఇప్పుడు ∆ACD మరియు ∆CAB లలో
\(\angle \mathrm{DCA}=\angle \mathrm{CAB}\) మరియు \(\angle \mathrm{DAC}=\angle \mathrm{BCA}\)
అలాగే AC = CA(ఉమ్మడి భుజం)
అందువలన ∆ABC ≅ ∆CDA అయినది.
దీని అర్థం ఈ రెండు త్రిభుజాలు కో.భు.కో నియమము (కోణం, భుజం మరియు కోణం) ప్రకారం సర్వసమానాలు. అందుచే కర్ణం AC సమాంతర చతుర్భుజాన్ని రెండు సర్వసమాన పటాలుగా విభజించిందని చెప్పవచ్చు.
![]()
2. సమాంతర చతుర్భుజము ఎదుటి భుజాలు సమానము. (పేజీ నెం. 180)
సాధన.
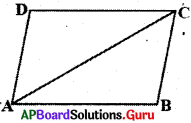
కర్ణం, సమాంతర చతుర్భుజాన్ని రెండు సర్వసమాన త్రిభుజాలుగా విభజిస్తుందని మనం నిరూపించాం.
పటంలో ∆ACD ≅ ∆CAB అయినది.
అందువలన AB = DC మరియు \(\angle \mathrm{CBA}=\angle \mathrm{ADC}\) అగును.
అలాగే AD = BC మరియు \(\angle \mathrm{DAC}=\angle \mathrm{ACB}\)\(\angle \mathrm{CAB}=\angle \mathrm{DCA}\)
∴ \(\angle \mathrm{ACB}+\angle \mathrm{DCA}=\angle \mathrm{DAC}+\angle \mathrm{CAB}\) అందుచే \(\angle \mathrm{DCB}=\angle \mathrm{DAB}\)
దీని నుండి సమాంతర చతుర్భుజంలో
(i) ఎదుటి భుజాలు సమానమని
(ii) ఎదుటి కోణాలు సమానమని చెప్పవచ్చు.
3. ఒక చతుర్భుజములో ప్రతి ఇత ఎదుటి భుజాలు సమానము అయితే, అది సమాంతర చతుర్భుజమగును. (పేజీ నెం. 180)
సాధన.
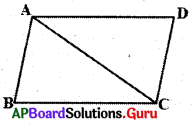
ABCD చతుర్భుజము AB = DC మరియు BC = AD అని తీసుకోండి. కర్ణం AC ను గీయండి.
త్రిభుజాలు ∆ABC మరియు ∆CDA పరిశీలించండి.
మనకు BC = AD, AB = DC మరియు AC = CA (ఉమ్మడి భుజం)
కావున ∆ABC ≅ ∆CDA
అందువలన \(\angle \mathrm{BCA}=\angle \mathrm{DAC}\), AC తిర్యగ్రేఖతో కలసి ఉన్నందున AB || DC అగును. ……. (1)
ఇదే విధంగా \(\angle \mathrm{ACD}=\angle \mathrm{CAB}\), CA తిర్యగ్రేఖలో కలిసి ఉన్నందున BC || AD అయినది. …….. (2)
(1), (2) లను బట్టి ABCD ఒక సమాంతర చతుర్భుజము అయినది.
4. ఒక చతుర్భుజములో ప్రతి జత ఎదుటి కోణాలు సమానము అయితే అది సమాంతర చతుర్భుజము. (పేజీ నెం.181)
సాధన.
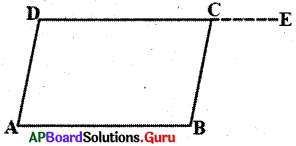
ABCD చతుర్భుజములో \(\angle \mathrm{A}=\angle \mathrm{C}\) మరియు \(\angle \mathrm{B}=\angle \mathrm{D}\) అయిన ABCD సమాంతర చతుర్భుజమని నిరూపించాలి.
\(\angle \mathrm{A} + \angle \mathrm{B} + \angle \mathrm{C} + \angle \mathrm{D}\) = 360° అని మనకు తెలుసు.
∴ \(\angle \mathrm{A} + \angle \mathrm{B} + \angle \mathrm{C} + \angle \mathrm{D}\) = \(\frac {360°}{2}\)
అదే విధంగా, \(\angle \mathrm{A} + \angle \mathrm{B}\) = 180°
DC ని E వైపు పొడిగించగా,
\(\angle \mathrm{C} + \angle \mathrm{BCE}\) = 180° కావున \(\angle \mathrm{BCE}=\angle \mathrm{ADC}\) అగును.
\(\angle \mathrm{BCE}=\angle \mathrm{D}\) అయితే AD || BC (ఎందుకు ?)
DC ని తిర్యగ్రేఖగా తీసుకో అదే విధంగా AB || DC అని నిరూపించవచ్చు.
కావున ABCD సమాంతర చతుర్భుజము అయినది.
![]()
5. సమాంతర చతుర్భుజములో కర్ణాలు పరస్పరము సమద్విఖండన చేసుకుంటాయి. (పేజీ నెం. 181)
సాధన.
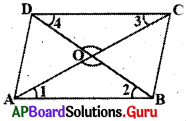
ABCD సమాంతర చతుర్భుజము గీయాలి.
రెండు కర్ణాలు AC మరియు BD లు ‘O’ వద్ద ఖండించుకున్నట్లు గీయాలి.
∆OAB మరియు ∆OCD లలో
పటంలో ఏర్పడిన కోణాలను \(\angle 1, \angle 2, \angle 3, \angle 4\)గా గుర్తించాలి.
\(\angle 1=\angle 3\) (AB || CD మరియు AC తిర్యగ్రేఖ చేసిన ఏకాంతర కోణాలు)
\(\angle 2=\angle 4\) (ఎలా ?) (ఏకాంతర కోణాలు)
మరియు AB = CD (సమాంతర చతుర్భుజ ధర్మం)
కావున కో.భు.కో. త్రిభుజ సర్వసమానత్వ నియమం ప్రకారం
∆OCD ≅ ∆OAB అగును.
అందువలన CO = OA, DO = OB అయినవి. అంటే కర్ణములు పరస్పరం సమద్విఖండన చేసుకున్నవి. మనం ఇప్పుడు దీని విపర్యయం కూడా సత్యమో, కాదో పరిశీలిద్దాం. అంటే దీని విపర్యయం “ఒక చతుర్భుజము కర్ణములు పరస్పరము సమద్విఖండన చేసుకుంటే, ఆది సమాంతర చతుర్భుజం” అవుతుంది.
6. ఒక చతుర్భుజంలో కర్ణములు పరస్పరం సమద్విఖండన చేసుకుంటే అది సమాంతర చతుర్భుజము అగును. (పేజీ నెం. 182)
సాధన.
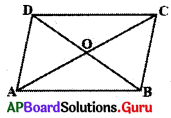
ABCD ఒక చతుర్భుజం.
AC, BD కర్ణాలు ‘O’ వద్ద ఖండించుకున్నాయి.
OA = OC, OB = OD అగునట్లు
మనం ABCD ని ఒక సమాంతర చతుర్భుజమని చూపాలి.
7. ఒక త్రిభుజములో రెండు భుజాల మధ్య బిందువులను కలుపుతూ గీయబడిన రేఖ, మూడవ భుజానికి సమాంతరముగానూ, మరియు దానిలో సగము ఉంటుంది. (పేజీ నెం. 188)
సాధన.
∆ABC లో AB మధ్యబిందువు E మరియు AC మధ్య బిందువు F.
సారాంశం:
(i) EF || BC
(ii) EF = \(\frac {1}{2}\)BC
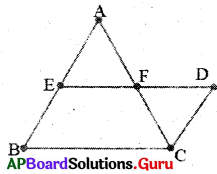
ఉపపత్తి : EF ను ని కలిపి పొడిగించి BAకు సమాంతరంగా C నుండి ఒక రేఖను గీస్తే, అది పొడిగించిన EF రేఖను D వద్ద ఖండిస్తుంది. ∆AEF మరియు ∆CDF
AF = CF (AC మధ్యబిందువు)
\(\angle \mathrm{AFE}=\angle \mathrm{CFD}\) (శీర్షాభిముఖ కోణాలు)
మరియు \(\angle \mathrm{AEF}=\angle \mathrm{CDF}\) (CD || BA తో ED తిర్యగ్రేఖ చేసిన ఏకాంతర కోణాలు)
కో. భు, కో, సర్వసమానత్వ నియమము ప్రకారం
∴ ∆AEF ≅ ∆CDF అయినది.
కావున AE = CD మరియు EF = DF (సర్వసమాన త్రిభుజాల సరూపభాగాలు)
AE = BE అని మనకు ఇవ్వబడింది.
కనుక BE = CD అయింది.
BE || CD మరియు BE = CD కావున BCDE ఒక సమాంతర చతుర్భుజము అయినది.
అందుచే ED || BC
⇒ EF || BC
BCDE సమాంతర చతుర్భుజము కావున ED = BC (ఎలా ?) (∵ DF = EF)
FD = EF అని చూపినందున
∴ 2EF = BC అగును. అందువలన EF = \(\frac {1}{2}\)BC అయినది.
![]()
8. ఒక త్రిభుజములో ఒక భుజము యొక్క మధ్య బిందువు నుండి వేరొక భుజానికి సమాంతరముగా గీయబడిన రేఖ, మూడవ భుజాన్ని సమద్విఖండన చేస్తుంది. (పేజీ నెం. 189)
సాధన.
∆ABC గీయాలి. AB మధ్య బిందువుగా Eని గుర్తించాలి. E గుండా BC కి సమాంతరముగా ‘l’ అనే రేఖను గీయాలి. ఇది AC ని F వద్ద ఖండించిందని అనుకుందాము.
CD || BA ను నిర్మించాలి. మనం AF = CF అని చూపాలి.
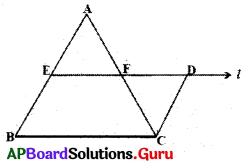
అందుచే ∆AEF మరియు ∆CFD లను తీసుకోండి.
\(\angle \mathrm{EAF}=\angle \mathrm{DCF}\) (BA || CD మరియు AC తిర్యగ్రేఖ) (ఎలా ?)
\(\angle \mathrm{AEF}=\angle \mathrm{D}\)
(BA || CD మరియు ED తిర్యగ్రేఖ) (ఎలా ?)
కాని ఏవైనా రెండు భుజాలను సమానంగా చూపలేదు. కావున మనం వీటిని సర్వసమాన . త్రిభుజాలని చెప్పలేము.
అందువలన EB || DC మరియు ED || BC తీసుకోండి. కావున EDCB ఒక సమాంతర చతుర్భుజము అయినది. దీని నుండి BE = DC అయినది.
కాని BE = AE కావున మనకు AE = DC అని వచ్చింది. అందుచే కో.భు. కో. నియమం ప్రకారము
∆AEF ≅ ∆CFD అయినది.
∴ AF = CF అగును.
ఉప సిద్ధాంతాలు
1. దీర్ఘచతురస్రంలో ప్రతీకోణము లంబకోణము అని నిరూపించండి. (పేజీ నెం. 182)
సాధన.
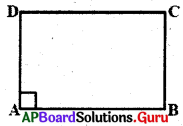
దీర్ఘచతురస్రమనేది ఒక సమాంతర చతుర్భుజము మరియు ఒక కోణము లంబకోణము.
ABCD ఒక దీర్ఘచతురస్రము.
ఒక కోణం \(\angle \mathrm{A}\) = 90° అనుకోండి.
మనం \(\angle \mathrm{B}=\angle \mathrm{C}=\angle \mathrm{D}\) = 90° అని చూపాలి.
ABCD సమాంతర చతుర్భుజము.
కావున AD || BC మరియు AB తిర్యగ్రేఖ
కావున \(\angle \mathrm{A}+\angle \mathrm{B}\) = 180° (తిర్యగ్రేఖకు ఒకే వైపునగల అంతరకోణాల మొత్తం) కాని \(\angle \mathrm{A}\) = 90° (తీసుకోబడింది)
∴ \(\angle \mathrm{B}\) = 180° – \(\angle \mathrm{A}\)
= 180° – 90° = 90°
ఇప్పుడు \(\angle \mathrm{C}=\angle \mathrm{A}\) మరియు \(\angle \mathrm{D}=\angle \mathrm{B}\) (సమాంతర చతుర్భుజంలో)
కావున \(\angle \mathrm{C}\) = 90° మరియు \(\angle \mathrm{D}\) = 90° అయింది. అందుచే దీర్ఘచతురస్రములో ప్రతికోణం లంబకోణము అగును.
![]()
2. రాంబలో కర్ణాలు పరస్పరం లంబాలుగా ఉంటాయని చూపండి. (పేజీ నెం.183)
సాధన.
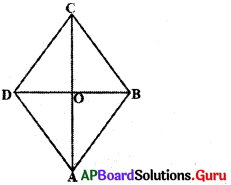
అన్ని భుజాలు సమానంగా గల సమాంతర చతుర్భుజమును రాంబస్ అంటారని మీకు తెలుసు. ABCD ఒక రాంబస్ AC మరియు BD .కరాలు O వద్ద ఖండించుకున్నాయనుకొనండి.
మనం AC కర్ణం, BD కర్ణానికి లంబంగా ఉంటుందని చూపాలి.
∆AOB మరియు ∆BOC లను తీసుకొండి
OA = OC (సమాంతర చతుర్భుజము కర్ణాలు పరస్పరం)
OB = OB(∆AOB మరియు ∆BOC ఉమ్మడి భుజం)
AB = BC (రాంబన్లో భుజాలు)
అందువలన ∆AOB ≅ ∆BOC (డు.భు.భు. నియమము)
కావున \(\angle \mathrm{AOB}=\angle \mathrm{BOC}\)
కాని \(\angle \mathrm{AOB}+\angle \mathrm{BOC}\) = 180° (రేఖీయద్వయం)
అందుచే 2\(\angle \mathrm{AOB}\) = 180°
లేదా \(\angle \mathrm{AOB}\) = \(\frac {180°}{2}\) = 90°
ఈ విధంగా \(\angle \mathrm{BOC}=\angle \mathrm{COD}=\angle \mathrm{AOD}\) = 90° అయినది.
కావున AC కర్ణం, BD కర్ణానికి లంబం అని తెలిసింది.
అందుచే రాంబస్ లో కర్ణాలు ఒకదానికొకటి లంబంగా ఉంటాయి.
3. ABCD సమాంతర చతుర్భుజములో AC కర్ణం \(\angle \mathrm{A}\)ను సమద్విఖండన చేస్తే ABCD ఒక రాంబస్ అవుతుందని నిరూపించండి. (పేజీ నెం. 183)
సాధన.
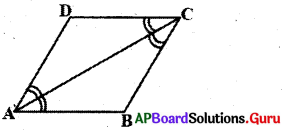
ABCD ఒక సమాంతర చతుర్భుజము.
అందుచే AB || DC. AC తిర్యగ్రేఖ \(\angle \mathrm{A}\), \(\angle \mathrm{C}\) లను ఖండించింది.
ఈ కావున \(\angle \mathrm{BAC}=\angle \mathrm{DCA}\) (ఏకాంతర కోణాలు) …………. (1)
\(\angle \mathrm{BAC}=\angle \mathrm{DAC}\) …………. (2)
కాని AC కర్ణం, \(\angle \mathrm{A}\)ను సమద్విఖండన చేసింది. కనుక \(\angle \mathrm{BAC}=\angle \mathrm{DAC}\)
∴ \(\angle \mathrm{DCA}=\angle \mathrm{DAC}\) ………. (3)
అందుచే AC కర్ణం \(\angle \mathrm{C}\) ని కూడా సమద్విఖండన చేసింది.
(1), (2) మరియు (3) లను బట్టి, మనకు
\(\angle \mathrm{BAC}=\angle \mathrm{BCA}\)
ΔABCలో \(\angle \mathrm{BCA}\) అంటే BC = AB (సమద్విబాహు త్రిభుజము)
కాని AB = DC మరియు BC = AD (సమాంతర చతుర్భుజము ABCD లో ఎదుటి భుజాలు)
∴ AB = BC = CD = DA
ఈ విధంగా ABCD రాంబస్ అయినది.
![]()
4. దీర్ఘచతురస్రంలో కర్ణాలు సమానమని నిరూపించండి. (పేజీ నెం. 184)
సాధన.

ABCD ఒక దీర్ఘచతురస్రము AC మరియు BD లు వాని కర్ణాలు. మనకు AC = BD అని తెలియాలి.
ABCD దీర్ఘచతురస్రమంటే ABCD ఒక సమాంతర చతుర్భుజము మరియు దానిలో ప్రతీ కోణము ఒక లంబకోణము.
ΔABC మరియు ΔBAD లను తీసుకోండి.
AB = BA (ఉమ్మడి భుజం)
\(\angle \mathrm{B}\) = \(\angle \mathrm{A}\) = 90° (దీర్ఘచతురస్రములో ప్రతీ కోణం )
BC = AD (దీర్ఘచతురస్రములో ఎదుటి భుజాలు)
అందువలన ΔABC ≅ ΔBAD (యు.కో. భు, నియమం) అగును.
దీని నుండి, AC = BD లేదా దీర్ఘచతురస్రములో కర్ణాలు సమానమని చెప్పవచ్చు.
5. సమాంతర చతుర్భుజములో కోణ సమద్విఖండన రేఖలు దీర్ఘచతురస్రాన్ని ఏర్పరుస్తాయని చూపండి. (పేజీ నెం. 184)
సాధన.
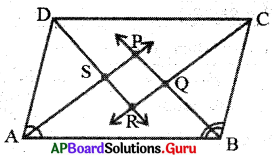
ABCD ఒక సమాంతర చతుర్భుజము \(\angle \mathrm{A},\angle \mathrm{B},\angle \mathrm{C}\) మరియు \(\angle \mathrm{A}\) యొక్క కోణ సమద్విఖండన రేఖలు P, Q, R, S ల వద్ద ఖండించుకొని చతుర్భుజాన్ని ఏర్పరిచాయి. (పటం చూడండి)
ABCD సమాంతర చతుర్భుజములో AD || BC, AB ని తిర్యగ్రేఖగా తీసుకుంటే,
\(\angle \mathrm{A}+\angle \mathrm{B}\) = 180° (సమాంతర చతుర్భుజములో పక్క కోణాలు)
కాని \(\angle \mathrm{BAP}\) = \(\frac {1}{2}\)\(\angle \mathrm{A}\) మరియు \(\angle \mathrm{ABP}\) = \(\frac {1}{2}\)\(\angle \mathrm{B}\)(AP, BP లు \(\angle \mathrm{A}\) మరియు \(\angle \mathrm{B}\) యొక్క సమద్విఖండన రేఖలు)
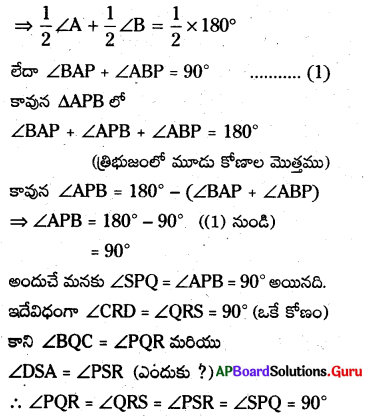
కావున PQRS లో నాలుగు కోణాలు 90° కు సమానము. అందుచే PQRS ను దీర్ఘచతురస్రమని చెప్పవచ్చు.
ఉదాహరణలు
1. ABCD సమాంతర చతుర్భుజము మరియు \(\angle \mathrm{A}\) = 60° మిగిలిన కోణాల కొలతలు కనుగొనండి. (పేజీ నెం.176)
సాధన.
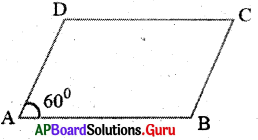
సమాంతర చతుర్భుజములో ఎదుటి కోణాలు సమానము. కావున ABCD సమాంతర చతుర్భుజము
\(\angle \mathrm{C}=\angle \mathrm{A}\) = 60° మరియు \(\angle \mathrm{B}=\angle \mathrm{D}\)
సమాంతర చతుర్భుజములో పక్క కోణాల మొత్తం 180°
\(\angle \mathrm{A}\) మరియు \(\angle \mathrm{B}\) లు పక్క కోణాలు కావున
\(\angle \mathrm{D}=\angle \mathrm{B}\) = 180° – \(\angle \mathrm{A}\)
= 180° – 60°
= 120°
అందుచే మిగిలిన కోణాలు 120°, 60°, 120° అవుతాయి.
![]()
2. ABCD సమాంతర చతుర్భుజము \(\angle \mathrm{DAB}\) = 40° అయిన మిగిలిన కోణాలను కనుగొనండి. (పేజీ నెం. 177)
సాధన.
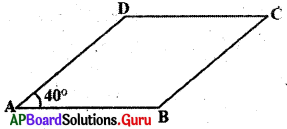
ABCD సమాంతర చతుర్భుజము కావున
\(\angle \mathrm{DAB}=\angle \mathrm{BCD}\) = 40° మరియు AC || BC ప్రక్క కోణాల మొత్తము
\(\angle \mathrm{CBA}=\angle \mathrm{DAB}\) = 180°
∴ \(\angle \mathrm{CBA} = 180 – 40° = 140°
దీనిద్వారా [latex]\angle \mathrm{ADC}\) = 140° అయితే \(\angle \mathrm{BCD}\) = 40°
3. సమాంతర చతుర్భుజములో రెండు ఆసన్నభుజాలు వరుసగా 4.5 సెం.మీ. మరియు 3 సెం.మీ. దాని చుట్టుకొలత కనుగొనుము. (పేజీ నెం. 177)
సాధన.
సమాంతర చతుర్భుజము ఎదుటి భుజాల కొలతలు – సమానము.
కావున మిగిలిన రెండు భుజాలు 4.5 సెం.మీ. మరియు 3 సెం.మీ. కలిగి ఉంటాయి.
కావున, దీని చుట్టుకొలత = 4.5 + 3 + 4.5 + 3
= 15 సెం.మీ.
4. ABCD సమాంతర చతుర్భుజములో పక్కకోణాలు \(\angle \mathrm{A}\) మరియు \(\angle \mathrm{B}\) యొక్క సమద్విఖందన రేఖలు P వద్ద ఖండించుకున్నాయి. ఆయిన \(\angle \mathrm{APB}\) = 90° అని చూపండి. (పేజీ నెం. 177)
సాధన.
ABCD ఒక సమాంతర చతుర్భుజము పక్క కోణాలు \(\angle \mathrm{A}\) మరియు \(\angle \mathrm{B}\) యొక్క సమద్విఖండన రేఖలు \(\overline{\mathrm{AP}}\) మరియు \(\overline{\mathrm{BP}}\) లు సమాంతర చతుర్భుజములో పక్క కోణాలు సంపూరకాలు కావున
\(\angle \mathrm{A}\) + \(\angle \mathrm{B}\) = 180°
\(\frac {1}{2}\)\(\angle \mathrm{A}\) + \(\frac {1}{2}\)\(\angle \mathrm{B}\) = \(\frac {180°}{2}\)
⇒ \(\angle \mathrm{PAB}\) + \(\angle \mathrm{PBA}\) = 90°
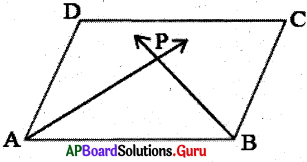
∆APB లో
\(\angle \mathrm{PAB}\) + APB + \(\angle \mathrm{PBA}\) = 180°
(త్రిభుజము మూడు కోణాల మొత్తము)
\(\angle \mathrm{APB}\) = 180° – (\(\angle \mathrm{PAB}\) + \(\angle \mathrm{PBA}\))
= 180° – 90°
= 90°
నిరూపించబడినది.
5. \(\overline{\mathrm{AB}}\) మరియు \(\overline{\mathrm{DC}}\) రెండు సమాంతర రేఖలు. తిర్యగ్రేఖ l, \(\overline{\mathrm{AB}}\) ని P వద్ద \(\overline{\mathrm{DC}}\) ని R వద్ద ఖండించింది. అయిన అంతరకోణాల సమద్విఖందన రేఖలు దీర్ఘచతురస్రాన్ని ఏర్పరుస్తాయని చూపండి.
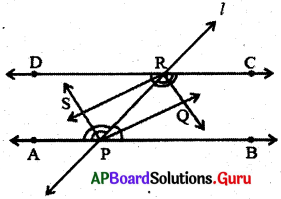
(పేజీ నెం. 185)
సాధన.
\(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{DC}}\), తిర్యగ్రేఖ l \(\overline{\mathrm{AB}}\) ని P వద్ద \(\overline{\mathrm{DC}}\) ని R వద్ద ఖండించింది.
\(\overline{\mathrm{PQ}}\), \(\overline{\mathrm{RQ}}\), \(\overline{\mathrm{RS}}\) మరియు \(\overline{\mathrm{PS}}\) లు \(\angle \mathrm{RPB},\angle \mathrm{CRP},\angle \mathrm{DRP}\) మరియు \(\angle \mathrm{APR}\)ల యొక్క సమద్విఖండన రేఖలు అనుకొనండి.
\(\angle \mathrm{BPR}=\angle \mathrm{DRP}\) (ఏకాంతర కోణాలు) ……. (1)
కాని \(\angle \mathrm{RPQ}\) = \(\frac {1}{2}\) \(\angle \mathrm{BPR}\)
(∵ \(\overline{\mathrm{PQ}}\), \(\angle \mathrm{BPR}\) యొక్క సమద్విఖండన రేఖ)
అలాగే \(\angle \mathrm{PRS}\) = \(\frac {1}{2}\)\(\angle \mathrm{DRP}\) (∵ \(\overline{\mathrm{RS}}\), \(\angle \mathrm{DRP}\) యొక్క సమద్విఖండన రేఖ) …………….. (2)
(1), (2) లను బట్టి
\(\angle \mathrm{RPQ}=\angle \mathrm{PRS}\)
ఇవి \(\overline{\mathrm{PR}}\) తిర్యగ్రేఖగా \(\overline{\mathrm{PQ}}\) మరియు \(\overline{\mathrm{RS}}\) రేఖలపై ఏర్పరచిన ఏకాంతర కోణాలు, కావున
∴ \(\overline{\mathrm{PQ}}\) || \(\overline{\mathrm{RS}}\)
ఇదేవిధంగా \(\angle \mathrm{PRQ}=\angle \mathrm{RPS}\) కావున \(\overline{\mathrm{PS}}\) || \(\overline{\mathrm{RQ}}\)
అందువలన PQRS ఒక సమాంతర చతుర్భుజం అయినది …………… (3)
మనకు \(\angle \mathrm{BPR}=\angle \mathrm{CRP}\) = 180° (తిర్యగ్రేఖ (l) ఒకే వైపున ఏర్పరచిన అంతరకోణాలు కావున \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{DC}}\))

(3), (4) లను బట్టి PQRS సమాంతర చతుర్భుజము మరియు
ప్రతీకోణము లంబకోణము అయినది. కావున PQRS ఒక దీర్ఘచతురస్రము.
![]()
6. ∆ABC లో BC భుజం మీదకు మధ్యగతం AD గీయబడినది. AD = ED అగునట్లు 5 వరకు పొదిగించబడినది. ఆయిన ABEC ఒక సమాంతర చతుర్భుజాన్ని నిరూపించండి. (పేజీ నెం. 186)
సాధన.
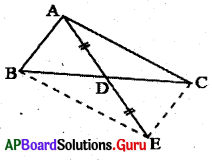
∆ABC త్రిభుజములో AD మధ్యగతం.
AD = ED అగునట్లు AD ని E వరకు పొడిగించబడింది.
BE మరియు CE లను కలపండి.
∆ABD మరియు ECD లలో
BD = DC (BC మధ్య బిందువు D)
\(\angle \mathrm{ADB}=\angle \mathrm{EDC}\) (శీర్షాభిముఖ కోణాలు)
AD = ED (ఇవ్వబడినది)
కావున ∆ABD ≅ ∆EDC అయినది. (భు.కో.భు. నియమము)
అందువలన AB = CE (సర్వసమాన త్రిభుజాలలో సరూప భాగాలు)
అలాగే \(\angle \mathrm{ABD}=\angle \mathrm{ECD}\)
ఇవి \(\overline{\mathrm{AB}}\) మరియు \(\overline{\mathrm{BC}}\) రేఖలతో \(\overline{\mathrm{CE}}\) తిర్యగ్రేఖ చేసిన ఏకాంతర కోణాలు.
∴ \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{CE}}\)
ABEC చతుర్భుజంలో
AB || CE మరియు AB = CE
అయినందున ABEC ఒక సమాంతర చతుర్భుజము అయినది.
7. ∆ABC లో D, E మరియు F లు వరుసగా AB, BC మరియు CA భుజాల మధ్యబిందువులు. వీటిని ఒకదానితో మరొకటి కలుపగా ఏర్పడిన నాలుగు త్రిభుజాలు సర్వసమానాలని చూపండి. (పేజీ నెం. 190)
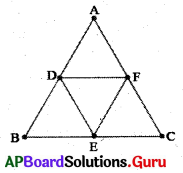
సాధన.
∆ABC లో D, E లు వరుసగా \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\) భుజాల మధ్యబిందువులు.
కావున మధ్యబిందువు సిద్ధాంతం ప్రకారము DE || AC
ఇదే విధంగా DF || BC మరియు EF || AB అగును.
అందువలన ADEF, BEFD మరియు CFDE లు సమాంతర చతుర్భుజాలు.
ఇప్పుడు ADEF సమాంతర చతుర్భుజములో DF కర్ణం.
కావున ∆ADF ≅ ∆DEF
(కర్ణం, సమాంతర చతుర్భుజాన్ని రెండు సర్వసమాన త్రిభుజాలుగా చేసింది)
ఇదే విధంగా ∆BDE ≅ ∆DEF మరియు ∆CEF ≅ ∆DEF అగును.
కనుక నాలుగు త్రిభుజాలు సర్వసమానములు అయినవి. దీని నుండి “త్రిభుజ భుజాల మధ్య బిందువులను కలుపగా ఏర్పడిన నాలుగు భుజాలు సర్వసమానములని” నిరూపించాము.
![]()
8. l, m మరియు n అనే మూడు సమాంతర రేఖలను ని మరియు qఅనే రెండు తిర్యగ్రేఖలు A, B, C మరియు D, E, F ల వద్ద ఖండించాయి. తిర్యగ్రేఖ p. ఈ సమాంతర రేఖలను రెండు సమాన అంతరఖండాలు AB, BC లుగా విభజిస్తే q తిర్యగ్రేఖ కూడా సమాన ఆంతరఖండాలు DE మరియు EF లుగా విభజిస్తుందని చూపండి. (పేజీ నెం. 191)
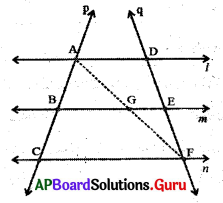
సాధన.
AB, BC మరియు DE, EF ల మధ్య సమానత్వ భావనతో సమన్వయ పరచాలి. A నుండి Fకు రేఖను గీయగా అది ‘m’ రేఖను G వద్ద ఖండించిందనుకొనండి.
∆ACF లో AB = BC (దత్తాంశము)
కావున AC మధ్యబిందువు B మరియు BG || CF (ఎలా ?) అందుచే AF యొక్క మధ్యబిందువు G అయినది (త్రిభుజ మధ్య బిందువు సిద్ధాంతం) , ఇప్పుడు ∆AFD ఇదే రీతిలో పరిశీలించగా G అనేది AF కు మధ్యబిందువు మరియు GE || AD కావున DF మధ్యబిందువు E ఆగును.
ఇందు మూలంగా DE = EF అయినది.
ఈ విధంగా I, m మరియు n రేఖలు q తిర్యగ్రేఖపై కూడా సమాన అంతర ఖండాలు చేసాయి.
9. ∆ABC లో AD మరియు BE లు రెండు మధ్యగత రేఖలు మరియు BE || DF (పటంలో చూడండి). అయిన CF = \(\frac {1}{4}\)AC అని చూపండి. (పేజీ నెం. 191)
సాధన.
∆ABC లో BC మధ్యబిందువు D మరియు BE || DF. మధ్యబిందువు సిద్ధాంతం ప్రకారము CE మధ్యబిందువు F అగును.
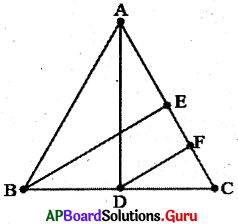
∴ CF = \(\frac {1}{2}\)CE
= \(\frac {1}{2}\) (\(\frac {1}{2}\)AC) (ఏలా ?
కావున CF = \(\frac {1}{4}\) AC అయినది.
![]()
10. ABCత్రిభుజంలో BC, CA మరియు AB భుజాలకు సమాంతరంగా A, B మరియు Cల గుండా సమాంతర రేఖలు గీస్తే అవి P,Q మరియు Rల వద్ద ఖండించు కున్నాయి. ∆PQR త్రిభుజము చుట్టుకొలత AABC త్రిభుజము చుట్టుకొలతకు రెట్టింపు ఉంటుందని చూపండి.
(పేజీ నెం.191)
సాధన.
AB || QP మరియు BC || RQ కావున ABCQ ఒక సమాంతర చతుర్భుజము.
ఇదే విధంగా BCAR, ABPC లు కూడా సమాంతర చతుర్భుజాలు అవుతాయి.
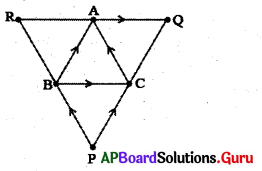
∴ BC = AQ మరియు BC = RA
⇒ QR మధ్యబిందువు A అగును.
ఇదేవిధంగా B, C లు వరుసగా PR మరియు PQల మధ్య బిందువులు అవుతాయి.
∴ AB = \(\frac {1}{2}\)PQ; BC = \(\frac {1}{2}\)QR మరియు
CA = \(\frac {1}{2}\) PR (ఎలా?) (సంబంధిత సిద్ధాంతం చెప్పండి)
ఇప్పుడు ∆PQR చుట్టుకొలత = PQ + QR + PR
= 2AB + 2BC + 2CA
= 2(AB + BC + CA)
= 2 (∆ABC యొక్క చుట్టుకొలత).