AP State Syllabus AP Board 9th Class Maths Solutions Chapter 6 Linear Equation in Two Variables Ex 6.3 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 6th Lesson Linear Equation in Two Variables Exercise 6.3
Question 1.
Draw the graph of each of the following linear equations.
i) 2y = – x + 1
ii) – x + y = 6
iii) 3x + 5y = 15
iv) \(\frac{x}{2}-\frac{y}{3}=3\)
Solution:
i) 2y = – x + 1
⇒ x + 2y = 1
ii) – x + y = 6
iii) 3x + 5y = 15
iv) \(\frac{x}{2}-\frac{y}{3}=3\)
⇒ \(\frac{3 x-2 y}{6}=3\)
⇒ 3x – 2y = 18
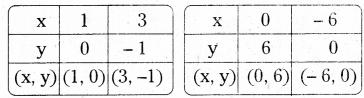

![]()
Question 2.
Draw the graph of each of the following linear equations and answer the following questions.
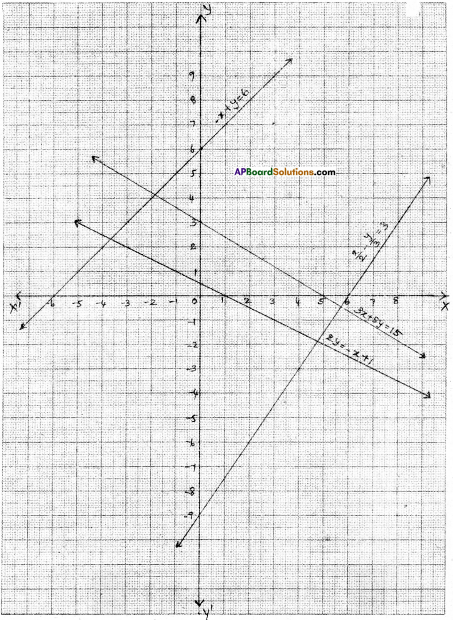
i) y – x
ii) y = 2x
iii) y = – 2x
iv) y = 3x
v) y = – 3x
Solution:
i) y = x
| x | 1 | 2 |
| y | 1 | 2 |
| (x, y) | (1, 1) | (2, 2) |
ii) y = 2x
| x | 1 | 2 |
| y | 2 | 4 |
iii) y = – 2x
| x | 1 | 2 |
| y | -2 | -4 |
iv) y = 3x
| x | 1 | 2 |
| y | 3 | 6 |
v) y = – 3x
| x | 1 | 2 |
| y | -3 | -6 |
![]()
i) Are all these equations of the form y = mx; where m is a real number ?
Solution:
Yes. All the equations are of the form y = mx where m e R.
ii) Are all these graphs passing through the origin ?
Solution:
Yes. All these lines pass through the origin.
iii) What can you conclude about these graphs ?
Solution:
All lines of the form y = mx, pass through the origin.
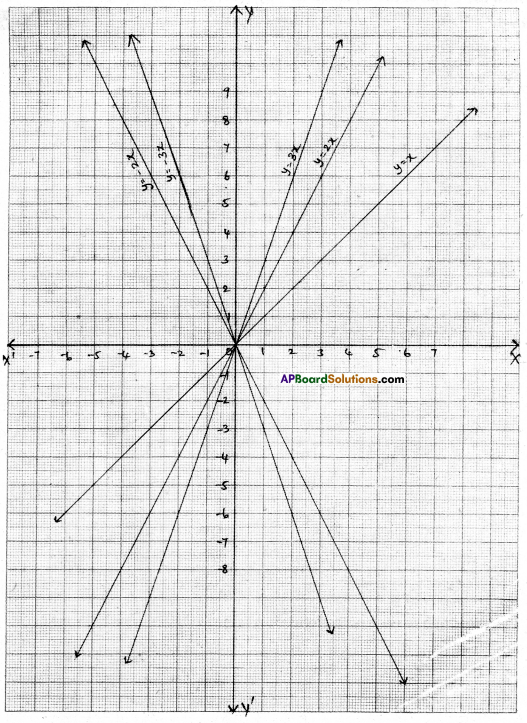
Question 3.
Draw the graph of the equation 2x + 3y = 11. Find from the graph value of y when x = 1.
Solution:
| x | 1 | 4 |
| y | 3 | 1 |
From the graph; when x = 1 then y = 3.
![]()
Question 4.
Draw the graph of the equation y – x = 2. Find from the graph
i) the value of y when x = 4
ii) the value of x when y = – 3
Solution:
The given equation is y – x = 2 or – x + y = 2
| x | 0 | -2 |
| y | 2 | 0 |
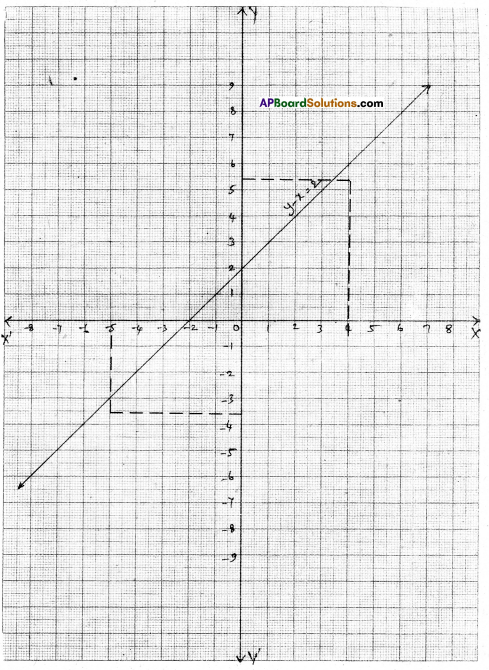
i) If x = 4 then y = 6 (∵ from the graph)
ii) When y = – 3 then x = – 5 (∵ from the graph)
Question 5.
Draw the graph of the equation 2x + 3y = 12. Find the solutions from the graph,
(i) Whose y-coordinate is 3 (OR) Whose y-coordinate is 2
(ii) Whose x-coordinate is – 3
Solution:
The given equation is 2x + 3y = 12
| x | 0 | 6 |
| y | 4 | 0 |
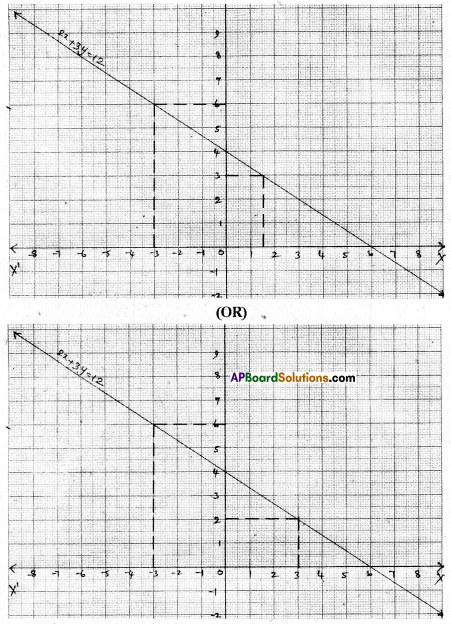
i) From the graph when y = 3 then 2x + 3(3) = 12 ⇒ 2x + 9 = 12 ⇒ 2x = 3 ⇒ x = \(\frac{3}{2}\) ; solution is (\(\frac{3}{2}\) , 3) (OR) When y = 2 then 2x + 3(2) = 12 ⇒ 2x + 6 = 12 ⇒ 2x = 6 ⇒ x = 3 solution is (3, 2),
ii) From the graph when x = – 3 then y = 6; solution is (- 3, 6)
![]()
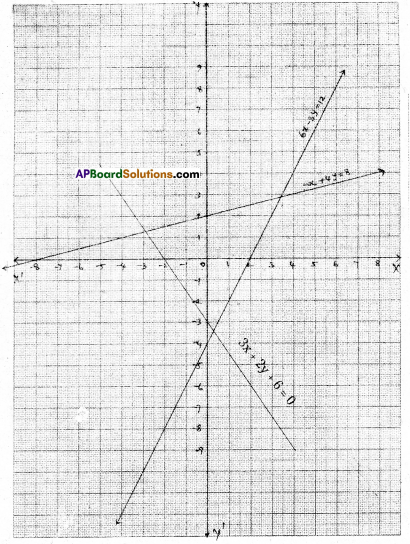
Question 6.
Draw the graph of each of the equations given below and also find the coordinates of the points where the graph cuts the coordinate axes.
i) 6x – 3y = 12
Solution:
6x – 3y = 12
| x | 0 | 2 |
| y | -4 | 0 |
From the graph the line cuts the X-axis at (2, 0) and Y-axis at (0, – 4).
ii) -x + 4y = 8
Solution:
| x | 0 | -8 |
| y | 2 | 0 |
From the graph the line cuts the X-axis at (- 8, 0) and Y -axis at (0, 2).
iii) 3x + 2y + 6 = 0
Solution:
3x + 2y + 6 = 0
| x | 0 | -2 |
| y | -3 | 0 |
From the graph the line cuts the X-axis at (- 2, 0) and Y -axis at (0, -3).
Question 7.
Rajiya and Preethi two students of class IX together collected ₹1000 for the Prime Minister Relief Fund for victims of natural calamities. Write a linear equation and
draw a graph to depict the statement. Clfp)
Solution:
Let Rajiya’s contribution to P.M.R.F be = ₹ x
Preethi’s contribution to P.M.R.F be = ₹ y
Then by problem x + y = 1000
| x + y = 1000 | ||
| x | 200 | 300 |
| y | 800 | 700 |
![]()
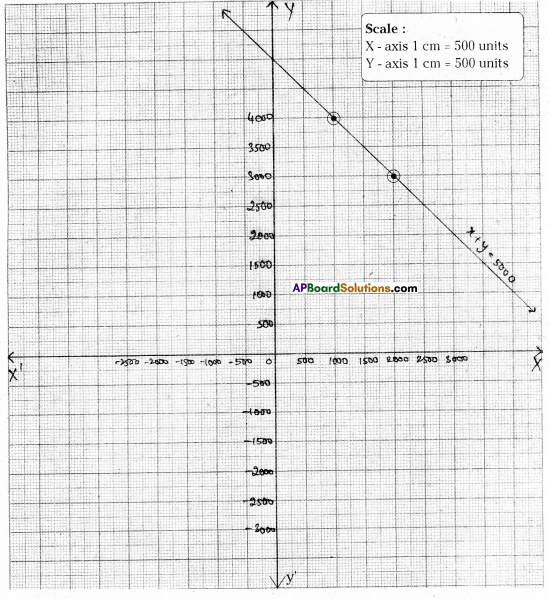
Question 8.
Gopaiah sowed w heat and paddy in two fields of total area 5000 sq. meters. Write a linear equation and draw a graph to represent the same.
Solution: Let the wheat be sowed in a land equal to x sq.m,
and the paddy be sowed in a land equal to y sq.m.
∴ By problem x + y = 5000
| x + y = 5000 | ||
| x | 1000 | 2000 |
| y | 4000 | 3000 |
Question 9.
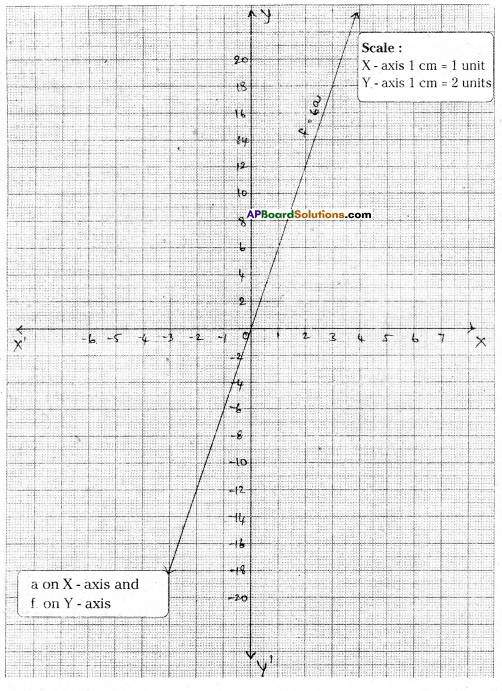
The force applied on a body of mass 6 kg. is directly proportional to the acceleration produced in the body. Write an equation to express this observation and draw the graph of the equation.
Solution:
Let the lorce = f; mass = 6 kg; acceleration = a
By problem f ∝ a or f = m . a ⇒ f = 6a
| f = 6a | ||
| a | 2 | 3 |
| f | 12 | 18 |
![]()
Question 10.
A stone is falling from a mountain. The velocity of the stone is given by v = 9.8t.
Draw its graph and find the velocity of the stone 4 seconds after start.
Solution:
Given that, the velocity of the stone v = 9.8 t
| v = 9.8t | ||
| v | 49 | 98 |
| t | 5 | 10 |
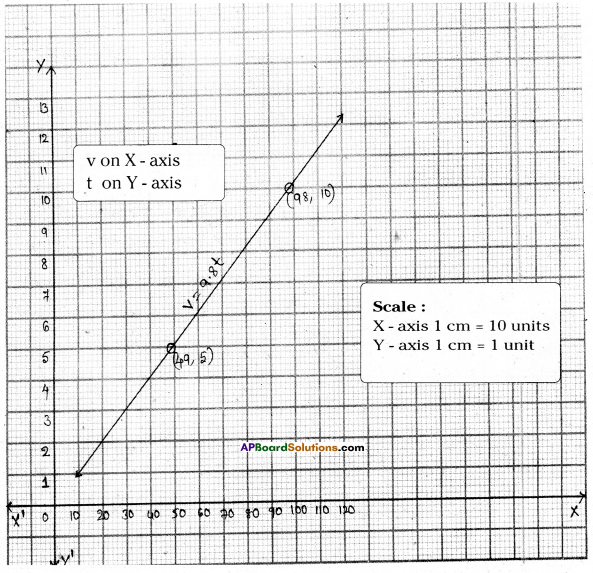
The velocity after 4 seconds = v = 9.8 × 4 = 39.2 m/sec2.
Question 11.
In an election 60 % of voters cast their votes. Form an equation and draw the graph for this data. Find the following from the graph.
i) The total number of voters, if 1200 voters cast their votes,
ii) The number of votes cast, if the total number of voters are 800.
[Hint: If the number of voters who cast their votes be ‘x’ and the total number of voters be ‘y’ then x = 60 % of y.]
Solution:
Let the total number of votes be = y
Then the number of voters who cast their votes = x
By problem x = 60 % of y
| x | 1200 | 480 |
| y | 2000 | 800 |
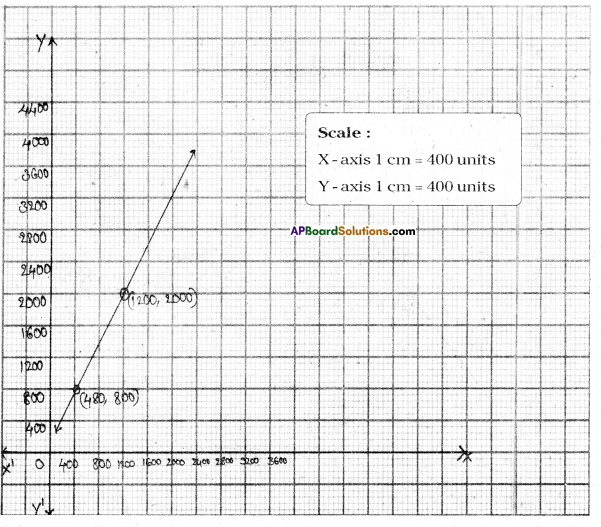
i) From the graph when x = 1200, then y = 2000
ii) From the graph when y = 800 then x = 480
![]()
Question 12.
When Rupa was born, her father was 25 years old. Form an equation and draw a graph for this data. From the graph find
i) The age of the father when Rupa is 25 years old.
ii) Rupa’s age when her father is 40 years old.
Solution:
Let her father’s age be = x years.
and Rupa’s age be = y years
By problem x – y = 25 years
| x | 40 | 50 |
| y | 15 | 25 |
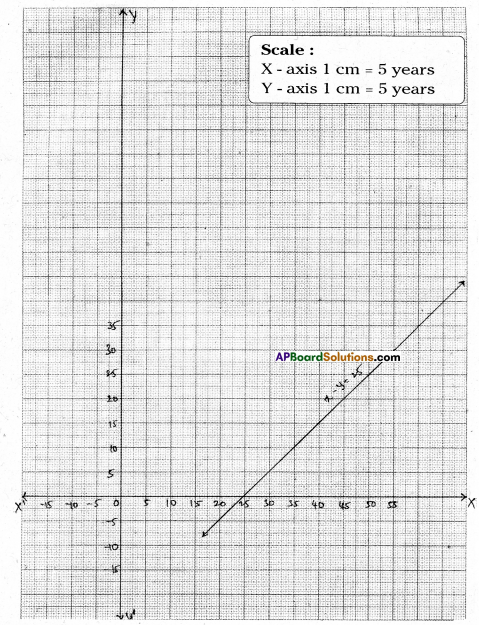
i) From the graph age of the father when Rupa is 25 years is 50 years.
ii) Rupa’s age when her father is 40 years is 15 years.
Question 13.
An auto charges ₹15 for first kilometre and ₹ 8 each for subsequent kilometre. For a distance of x km. an amount of ₹y is paid. Write the linear equation representing this information and draw the graph. With the help of graph find the distance travelled if the fare paid is ₹55. How much would have to be paid for 7 kilometres?
Solution:
Charge for the first kilometre = ₹15
Charge for the subsequent kilometres = ₹ 8 per km.
Amount paid = ₹ y when the distance travelled is x km
∴ By problem y = 15 + 8x
∴ 8x – y + 15 = 0
| x | 2 | 1 |
| y | 31 | 23 |
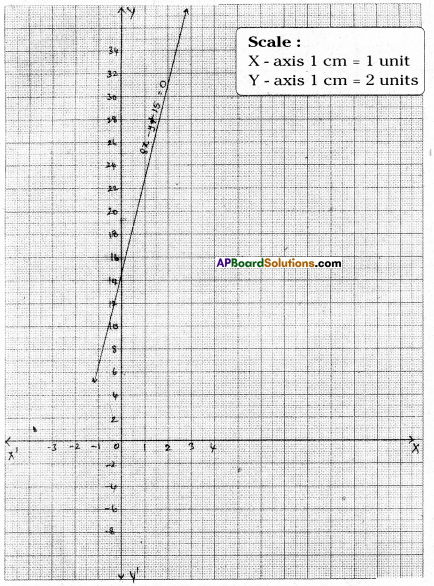
i) When y = 55 then x = 5
ii) From the graph when x = 7 then y = 71
![]()
Question 14.
A lending library has fixed charge for the first three days and an additional charges for each day thereafter. John paid ₹ 27 for a book kept for seven days. If the fixed charges be ₹ x and subsequent per day charges be ₹ y; then write the linear equation representing the above information and draw the graph of the same. From the graph if the fixed charge is ₹ 7, find the subsequent per day charge. And if the per day charge is ₹ 4, find the fixed charge, (charge is ₹7)
Solution:
John kept a book for 7 days. He paid ₹ 27
For first three days = ₹ x (fixed)
For the last four days = ₹ 4y (? y for a day)
By problem x + 4y = 27
| x | 3 | 11 | 7 |
| y | 6 | 4 | 5 |
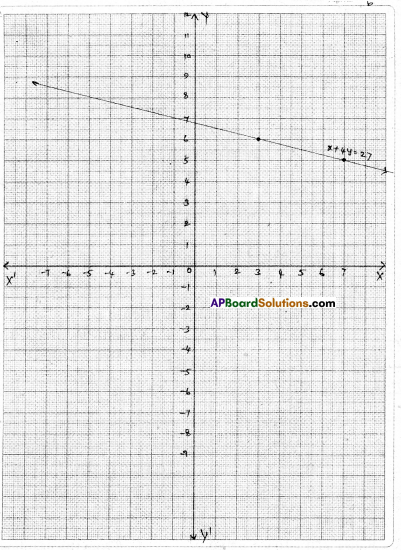
When x = 7 then y = 5
When y = 4 then x = 11
Question 15.
The parking charges of a car in Hyderabad Railway station for first two hours is ₹ 50 and ₹10 for each subsequent hour. Write down an equation and draw the graph. Find the following charges from the graph.
i) For three hours ii) For six hours iii) How many hours did Rekha park her car if she paid ₹ 80 as parking charges ?
Solution: Let the total money paid be = ₹ y
Parking charges for the first two hours = ₹ 50
Parking charges for total x hours @ ₹10 per hour = 50 + (x – 2) 10
= 50 + 10x – 20
= 10x + 30
∴ By problem y = 10x + 30
| x | 3 | 5 | 6 |
| y | 60 | 80 | 90 |
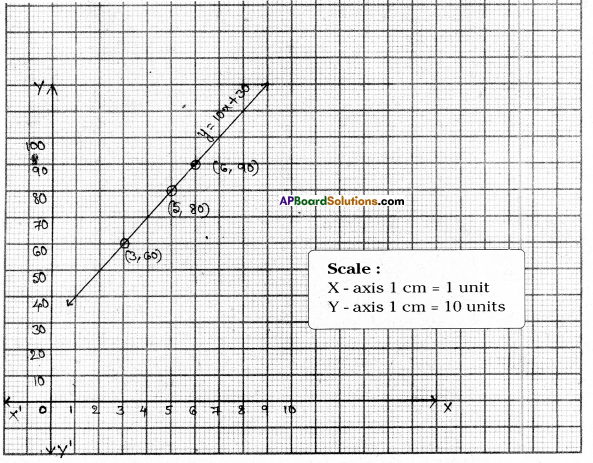
i) For three hours = 50 + 10 × 1 = ₹ 60
[ ∵ From the graph we see the same]
ii) For six hours = 50 + 10 × 4 = 50 + 40 = ₹ 90
iii) Rekha parked her car for 5 hours.
![]()
Question 16.
Sameera was driving a car with uniform speed of 60 kmph. Draw distance – time graph. From the graph find the distance travelled by Sameera in
i) \(\frac { 1 }{ 2 }\) hours
ii) 2 hours
iii) 3\(\frac { 1 }{ 2 }\) hours
Solution:
Speed of the car = 60 kmph
Let the time taken be = x hours
Then the total distance travelled be = y hours
By problem 60x = y or 60x – y = 0
| x | 2 | 4 | 5 |
| y | 120 | 240 | 300 |
ii) Distance travelled in 1\(\frac { 1 }{ 2 }\) hours = 120 km
ii) Distance travelled in 2 hours = 120 km
iii) Distance travelled in 3\(\frac { 1 }{ 2 }\) hours = 210 km
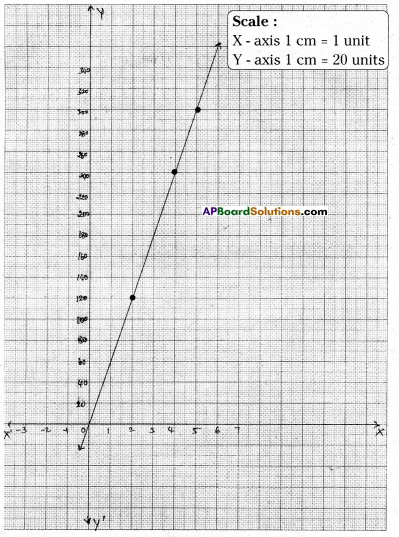
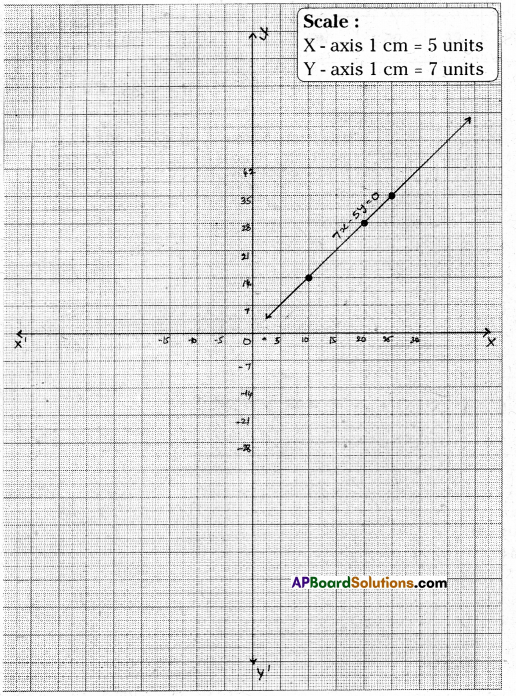
Question 17.
The ratio of molecular weight of Hydrogen and Oxygen in water is 1 : 8. Set up an equation between Hydrogen and Oxygen and draw its graph. From the graph find the quantity of Hydrogen if Oxygen is 12 grams. And quantity of Oxygen if
Hydrogen is \(\frac { 3 }{ 2 }\) grams.
[Hint : If the quantities of hydrogen and oxygen ‘x’ and ‘y’ respectively, then
x : y = 1 : 8 ⇒ 8x = y]
Solution:
Let the quantity of Hydrogen = x grams
And the quantity of Oxygen = y grams
By problem 8x = y ⇒ 8x – y = 0
| x | 1 | 2 | 4 | 5 |
| y | 8 | 16 | 32 | 40 |
From the graph, the quantity of Hydrogen if Oxygen is 12 gm = \(\frac { 3 }{ 2 }\) g.
From the graph, the quantity of Oxygen if Hydrogen is \(\frac { 3 }{ 2 }\) g = 12 g.
![]()
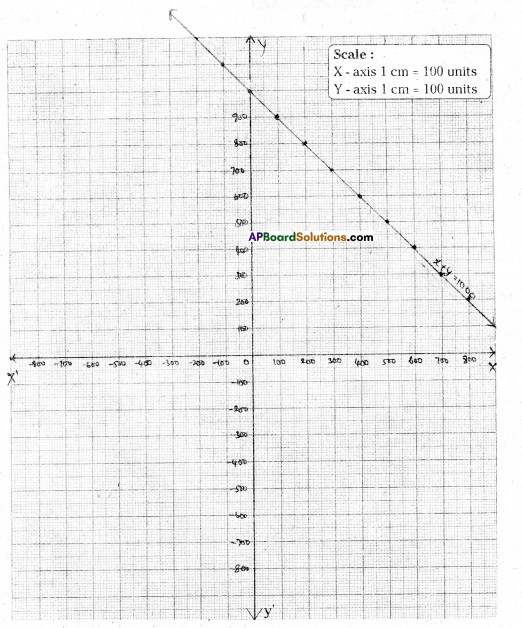
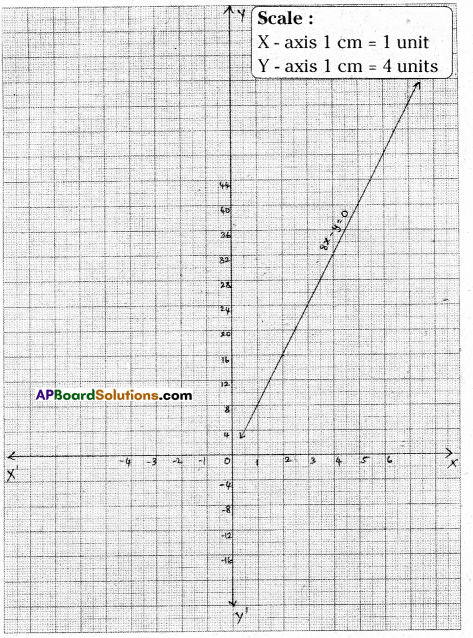
Question 18.
In a mixture of 28 litres, the ratio of milk and water is 5 : 2. Set up the equation between the mixture and milk. Draw its graph. By observing the graph find the quantity of milk in the mixture.
[Hint: Ratio between mixture and milk = 5 + 2:5 = 7:5]
Solution:
Let the quantity of milk in the mixture be = x lit.
quantity of the mixture = y lit.
Ratio of the milk and water = 5:2
Sum of the terms of the ratio = 5 + 2 = 7
Quantity of milk x = \(\frac { 5 }{ 7 }\) y lit.
7x = 5y ⇒ 7x – 5y = 0
| x | 10 | 20 | 25 |
| y | 14 | 28 | 35 |
From the graph quantity of milk in the mixture = 20 lit.
![]()
Question 19.
In countries like U.S.A. and Canada temperature is measured in Fahrenheit whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius F = \(\frac { 9 }{ 5 }\) C + 32
i) Draw the graph of the above linear equation having Celsius on X-axis and Fahrenheit on Y-axis.
ii) If the temperature is 30°C, what is the temperature in Fahrenheit ?
iii) If the temperature is 95°F, what is the temperature in Celsius ?
iv) Is there a temperature that has numerically the same value in both Fahrenheit and Celsius ? If yes, find it.
Solution:
i) Given that F = \(\frac { 9 }{ 5 }\) C + 32
| C | 20 | 30 | 35 | -40 |
| F | 68 | 86 | 95 | -40 |
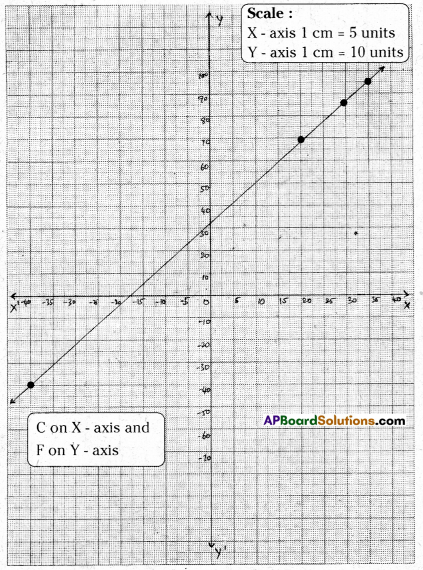
If C = 20, F = \(\frac { 9 }{ 5 }\) × 20 + 32 = 68
If c = 30, F = \(\frac { 9 }{ 5 }\) × 30 + 32 = 86
If C = 35, F = \(\frac { 9 }{ 5 }\) × 35 + 32 = 95
If C = -40, F = \(\frac { 9 }{ 5 }\) × (-40) + 32 = -40
ii) From the graph 30°C = 86°F
iii) 95°F = 35°C
iv) When C = – 40 then F = – 40