SCERT AP 9th Class Maths Solutions Chapter 4 సరళ రేఖలు మరియు కోణములు Ex 4.4 Textbook Exercise Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 4th Lesson సరళ రేఖలు మరియు కోణములు Exercise 4.4
ప్రశ్న 1.
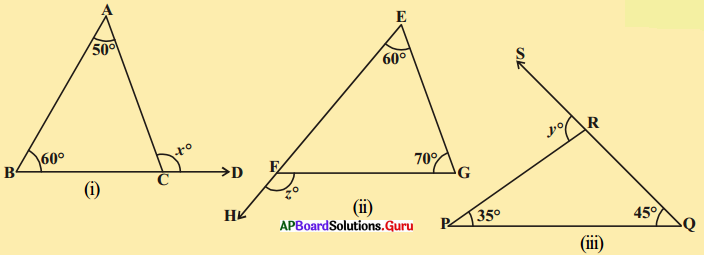
ఇచ్చిన త్రిభుజంలో x, y మరియు z ల విలువలను కనుగొనుము.
సాధన.
పటం (i) లో
x° = 50° + 60°
(∵ ఒక త్రిభుజంలో బాహ్య కోణము, అంతరాభిముఖ కోణాల మొత్తంకు సమానము)
∴ x = 110°
పటం (ii) లో
° = 60° + 70°
(∵ ఒక త్రిభుజంలో బాహ్య కోణము, అంతరాభిముఖ కోణాల మొత్తంకు సమానము)
∴ z = 130°
పటం (iii) లో
y° = 35° + 45° = 80°
∴ y° = 80°
(∵ ఒక త్రిభుజంలో బాహ్య కోణము, అంతరాభిముఖ కోణాల మొత్తంకు సమానము)
ప్రశ్న 2.
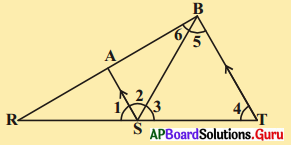
ఇచ్చిన పటంలో AS // BT; ∠4 = ∠5, ∠ASTని \(\overline{\mathrm{SB}}\) కోణసమద్విఖండన చేస్తుంది. అయిన ∠1 విలువను కనుగొనండి.
సాధన.
దత్తాంశము AS // BT.
∠4 = ∠5 మరియు \(\overline{\mathrm{SB}}\), ∠AST ను కోణసమద్వి ఖండన చేయును.
∴ లెక్క ప్రకారము ∠2 = ∠3 ………….. (1)
AS // BT రేఖల నుండి ∠2 = ∠5 (∵ ఏకాంతర కోణాలు)
∴ ΔBST లో ∠3 = ∠5 = ∠4 కావున
ΔBST ఒక సమబాహు త్రిభుజము మరియు ప్రతి కోణము 60° లుగా వుండును.
∴ ∠3 = ∠2 = 60° [సమీకరణము (1) నుండి]
ఇప్పుడు ∠1 + ∠2 + ∠3 = 180°
∴ ∠1 + 60° + 60° = 180°
[∵ ఒక రేఖ పై గల బిందువు వద్ద కోణములు]
∴ ∠1 = 180° – 120° = 60°
![]()
ప్రశ్న 3.
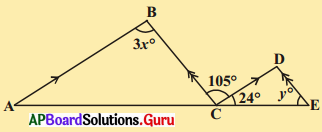
ఇచ్చిన పటంలో AB // CD; BC // DE అయిన x, y ల విలువలు కనుగొనండి.
సాధన.
దత్తాంశము నుండి AB // CD మరియు BC // DE.
∴ 3x = 105°
(∵ AB // CD కావున సమాంతర కోణములు)
x = \(\frac{105^{\circ}}{3}\) = 35°
అదే విధముగా BC // DE
∴ ∠D = 105° (∵ ఏకాంతర కోణములు)
ఇప్పుడు ΔCDE లో
24° + 105° + y = 180° (∵ కోణముల మొత్తము)
∴ y = 180° – 129° = 51°
ప్రశ్న 4.
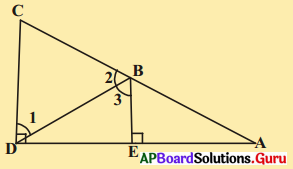
కింద పటంలో BE ⊥ DA మరియు CD ⊥ DA అని ఇవ్వబడినది. అయిన ∠1 ≅ ∠3 అని చూపండి.
సాధన.
దత్తాంశము ప్రకారము
BE ⊥ DA మరియు CD ⊥ DA.
⇒ CD మరియు BE లు DA రేఖకు లంబాలు.
⇒ CD // BE (లేక) ∠D = ∠E ⇒ CD // BE
(∵ CD, BE రేఖలకు DA తిర్యగ్రేఖ అయిన ఆసన్న కోణాలు సమానము)
ఇప్పుడు ∠1 = ∠3 అని (∵ ఏకాంతర కోణాలు) నిరూపించబడినది.
ప్రశ్న 5.
x, y ల ఏ విలువలకు, AD, BC రేఖలు సమాంతర రేఖలు అవుతాయి ?
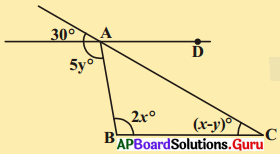
సాధన.
AD, BC రేఖలు సమాంతరాలు.
x – y = 30° …….. (1) (∵ ఆసన్న కోణాలు)
2x = 8y …………….. (2) (∵ ఏకాంతర కోణాలు)
(1) & (2) లను సాధించగా,

y = 10° ను సమీకరణము (1) లో ప్రతిక్షేపించగా,
x – 10° = 30° ⇒ x = 40°
∴ x = 40° మరియు y = 10°
![]()
ప్రశ్న 6.
పటంలో x, y ల విలువలు కనుగొనండి.
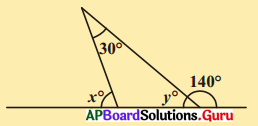
సాధన.
పటం నుండి y + 140° = 180° (∵ రేఖీయద్వయం)
∴ y = 180° – 140° = 40°
మరియు x° = 30° + y°
(∵ బాహ్యకోణము = అంతరాభిముఖ కోణాల మొత్తం)
x° = 30° + 40° = 70°
ప్రశ్న 7.
కింది పటంలో, బాణం గుర్తులచే సూచింపబడిన రేఖాఖండములు సమాంతరములు అయిన x, y ల విలువలు కనుగొనండి.
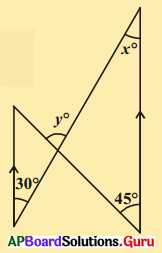
సాధన.
పటం నుండి
x° = 30° (∵ ఏకాంతర కోణాలు)
y° = 45° + x° (∵ బాహ్యకోణం = అంతరాభిముఖ కోణాల మొత్తము)
y = 45° + 30° = 75°
ప్రశ్న 8.
ఇచ్చిన పటంలో ∠PQR భుజాలు వరుసగా QP మరియు RQ, S మరియు T బిందువుల వద్దకు పొడిగించ బడ్డాయి. ∠SPR = 135°, ∠PQT = 110° అయిన ∠PRQ కొలతలు కనుగొనండి.
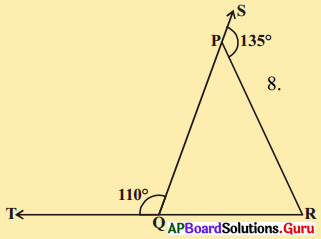
సాధన.
దత్తాశం నుండి ∠SPR = 135° మరియు ∠PQT = 110°
పటము నుండి,
∠SPR + ∠RPQ = 180°
∠PQT + ∠PQR = 180° [∵ రేఖీయద్వయం]
⇒ ∠RPQ = 180° – ∠SPR
= 180° – 135° = 45°
⇒ ∠PQR = 180° – ∠PQT.
= 180° – 110° = 70°
ΔPQRలో ∠RPQ + ∠PQR + ∠PRQ = 180°
∴ 45° + 70° + ∠PRQ = 180°
∴ ∠PRQ = 180° – 115° = 65°
![]()
ప్రశ్న 9.
ఇచ్చిన పటంలో ∠X = 62°; ∠XYZ = 54°. ΔXYZ లో ∠XYZ మరియు ∠XZY ల కోణ సమద్విఖండన రేఖలు వరుసగా YO మరియు ZO అయిన ∠OZY మరియు ∠YOZ ల కొలతలు కనుగొనండి.
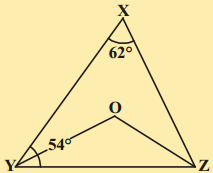
సాధన.
దత్తాంశం నుండి ∠X = 62° మరియు ∠Y = 54°
∠XYZల కోణ సమద్విఖండన రేఖలు వరుసగా YO మరియు ZO లు అగును.
ΔXYZలో
∠X + ∠XYZ + ∠XZY = 180°
62° + 54° + ∠XZY = 180°
⇒ ∠XZY = 180° – 116° = 64°
ΔOYZ లో
∠OYZ = \(\frac {1}{2}\)∠XYZ = \(\frac {1}{2}\) × 54° = 27
(∵ ∠XYZ యొక్క కోణ సమద్విఖండన రేఖ YO)
∠OZY = \(\frac {1}{2}\)∠XZY = \(\frac {1}{2}\) × 64° = 32°
(∵ ∠XYZ యొక్క కోణ సమద్విఖండన రేఖ OZ)
మరియు ∠OYZ + ∠OZY + ∠YOZ = 180°
⇒ 27° + 32° + ∠YOZ = 180°
⇒ ∠YOZ = 180° – 59° = 121°
ప్రశ్న 10.
ఇచ్చిన పటంలో AB || DE, ∠BAC = 35° మరియు ∠CDE = 53° అయిన ∠DCE కొలతలు కనుగొనండి.
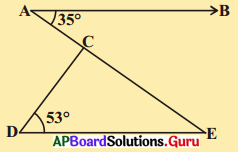
సాధన.
దత్తాంశం ప్రకారం AB || DE, ∠BAC = 35° మరియు ∠CDE = 53°
∠BAC = ∠E = 35° (∵ ఏకాంతర కోణాలు)
ΔCDE లో
∠C + ∠D + ∠E = 180°
∴ ∠DCE + 53° + 35° = 180°
⇒ ∠DCE = 180° – 88° = 92°
ప్రశ్న 11.
ఇచ్చిన పటంలో PQ, RS లు T బిందువు వద్ద ఖండించు కొంటాయి. ∠PRT = 40°, ∠RPT = 95° మరియు ∠TSQ = 75° అయిన కొలతలు కనుగొనండి.
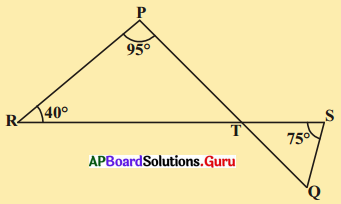
సాధన.
దత్తాంశం నుండి ∠PRT = 40°; ∠RPT = 95%; మరియు ∠TSQ = 75°
ΔPRT లో ∠P + ∠R + ∠PTR = 180° (∵ త్రిభుజ కోణాల ధర్మం )
95° + 40° + ∠PTR = 180°
⇒ ∠PTR = 180° – 135° = 45°
∴ ∠PTR = ∠STQ (∵ శీర్షాభిముఖ కోణాలు)
ΔSTQ లో ∠S + ∠Q + ∠STQ = 180° (∵ త్రిభుజ కోణాల ధర్మం)
75° + ∠SQT + 45° = 180°
∴ ∠SQT = 180° – 120° = 60°
![]()
ప్రశ్న 12.
కింది పటంలో ΔABC లో ∠B = 50° మరియు ∠C = 70°. AB, AC భుజాలు పొడిగించగా ఏర్పడిన బాహ్యకోణాల కోణసమద్విఖండన రేఖలు ఖండించుకొనగా ‘z’ ఏర్పడినది. ‘z’ విలువను కనుగొనండి.
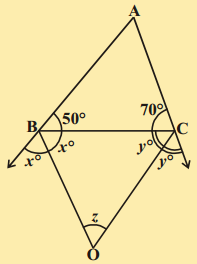
సాధన.
దత్తాంశం నుండి ΔABC లో ∠B = 50° మరియు ∠C = 70°
AB, AC లను పొడిగించగా ఏర్పడిన, బాహ్యకోణాల కోణ సమద్విఖండన రేఖలు ఖండించుకొనగా z ఏర్పడినది.
పటం నుండి 50° + 2x = 180°
70° + 2y = 180
∴ 2x = 180° – 50
2x = 130°
x = \(\frac{130^{\circ}}{2}\)
= 65°
2y = 180° – 70°
2y = 110°
y = \(\frac{110^{\circ}}{2}\)
= 55°
ΔBOC లో x + y + z = 180°
65° + 55° + z = 180°
z = 180° – 120° = 60°
ప్రశ్న 13.
ఇచ్చిన పటంలో PQ ⊥ PS, PQ // SR, ∠SQR = 28° మరియు ∠QRT = 65° అయిన x, y విలువలు కనుగొనుము.
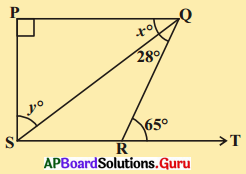
సాధన.
దత్తాంశం నుండి PQ ⊥ PS; PQ // SR
∠SQR = 28°, ∠QRT = 65°
పటం నుండి ∠QSR = x° (∵ PQ // SR రేఖల ఏకాంతర కోణాలు)
65° = x + 28° (∵ బాహ్యకోణం = అంతరాభిముఖ కోణాల మొత్తం)
∴ x° = 65° – 28° = 37°
మరియు x° + y° = 90°
[∵ PQ ⊥ PS మరియు PQ // SR ⇒ ∠P = ∠S]
37° + y = 90°
∴ y = 90° – 37° = 53°
![]()
ప్రశ్న 14.
ఇచ్చిన పటంలో ΔABC భుజం AC బిందువు D వరకు పొడిగించబడినది. ∠BCD = 125° అయిన ∠A : ∠B = 2 : 3 అయిన m ∠A, m ∠B లను కనుగొనండి.
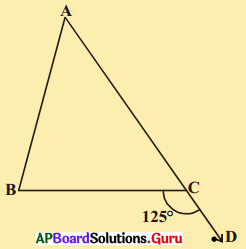
సాధన.
దత్తాంశం నుండి, ∠BCD = 125°
ΔABC లో భుజం AC బిందువు D వరకు పొడిగించబడినది.
∠A : ∠B = 2 : 3
నిష్పత్తిలో పదాల మొత్తము = 2 + 3 = 5
ఒక త్రిభుజంలో బాహ్యకోణము = అంతరాభిముఖ కోణాల మొత్తము
∠BCD = ∠A + ∠B
∠A = \(\frac {2}{5}\) × 125° = 50°
∠B = \(\frac {3}{5}\) × 125° = 75°
ప్రశ్న 15.
కింది పటంలో. BC // DE, ∠BAC = 35° మరియు ∠BCE = 102° అని ఇవ్వబడినది. అయిన i) ∠BCA ii) ∠ADE మరియు iii) ∠CED ల కొలతలు కనుగొనండి.
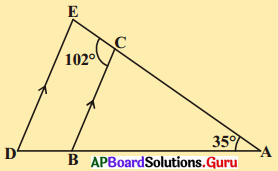
సాధన.
దత్తాంశము నుండి BC // DE ; ∠BAC = 35° మరియు ∠BCE = 102°
i) పటం నుండి
102° + ∠BCA = 180° (∵ రేఖీయద్వయం)
∴ ∠BCA = 180° – 102° = 78°
ii) ∠ADE + ∠CBD = 180°
(∵ తిర్యగ్రేఖకు ఒకే వైపున్న అంతరకోణాలు)
∠ADE + (78° + 35°) = 180°
(∵ ∠CBD = ∠BAC + ∠BCA)
∴ ∠ADE = 180° – 113° = 67°
iii) పటముల నుండి
∠CED = ∠BCA = 78° (∵ ఏక అంతర కోణాలు)
ప్రశ్న 16.
కింది పటంలో AB = AC; ∠BAC = 36%; ∠ADB = 45° మరియు ∠AEC = 40° అని ఇవ్వబడినది. అయిన i) ∠ABC ii) ∠ACB iii) ∠DAB iv) ∠EACల విలువలు కనుగొనండి.
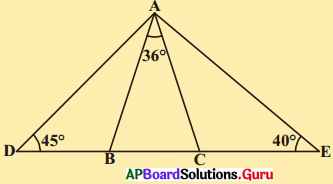
సాధన.
దత్తాంశం నుండి AB = AC, ∠BAC = 36°,
∠ADB = 45°, ∠AEC = 40°
(i) & (ii)
ΔABC లో AB = AC
⇒ ∠ABC = ∠ACB
మరియు త్రిభుజ కోణాల ధర్మం ప్రకారం
36° + ∠ABC + ∠ACB = 180°
∴ ∠ABC = \(\frac{180^{\circ}-36^{\circ}}{2}=\frac{144^{\circ}}{2}\) = 72°
∠ACB = 72°
iii) పటం నుండి
∠ABD + ∠ABC = 180°
∠ABD = 180° – 72° = 108°
ΔABD లో ∠DAB + ∠ABD + ∠D = 180°
∠DAB + 108° + 45° = 180°
∠DAB = 180° – 153° = 27°
iv) ΔADE లో
∠D + ∠A + ∠E = 180°
45° + ∠A + 40° = 180°
⇒ ∠A = 180° – 85° = 95°
∠A = ∠DAB + 36° + ∠EAC
95° = 27° + 36° + ∠EAC
∴ ∠EAC = 95° – 63° = 32°
![]()
ప్రశ్న 17.
ఇచ్చిన పటములోని సమాచారము ఆధారంగా x, y విలువలు కనుగొనుము.
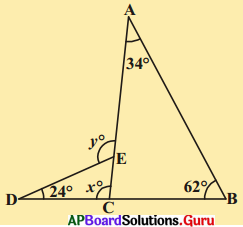
సాధన.
పటం నుండి ΔACB లో
34° + 62° + ∠ACB = 180°
∴ ∠ACB = 180° – 96° = 84°
మరియు x + ∠ACB = 180° (∵ రేఖీయద్వయం)
x + 84° = 180°
x = 180° – 84° = 96°
(లేదా)
x = 34° + 62° = 96° (∵ ΔABC లో x బాహ్య కోణము)
y = 24° + x°
= 24° + 96° = 120°
(∵ ΔDCE లో y బాహ్య కోణము)