SCERT AP 9th Class Maths Solutions Chapter 3 జ్యామితీయ మూలాలు InText Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 3rd Lesson జ్యామితీయ మూలాలు InText Questions
ఉదాహరణలు
1. A, B మరియు Cలు ఒకే సరళరేఖపై గల బిందువులు, B బిందువు A మరియు C ల మధ్య ఉన్నచో AC – AB = BC అని నిరూపించుము. (పేజీ నెం. 66)
![]()
సాధన.
AC మరియు AB + BC లు ఏకీభవిస్తాయి.
యూక్లిడ్ – 4 వ సాధారణ భావం ద్వారా “ఒక దానితో మరొకటి ఏకీభవించునవి సమానాలు” కావున AB + BC = AC అని చెప్పవచ్చు.
దీనిని AC లో ప్రతిక్షేపించగా AC – AB = BC
![]()
ఇక్కడ మనం రెండు బిందువుల గుండా ఒకే ఒక రేఖ ఉంటుందని తీసుకొనుటను గమనించండి.
2. ఇచ్చిన ఏ రేఖాఖండము పైన అయినా సమబాహు త్రిభుజం నిర్మించవచ్చు అని నిరూపించండి. (పేజీ నెం. 66)
సాధన.
ఏదేని పొడవు గల ఒక రేఖాఖండము PQ ఇవ్వబడినది.
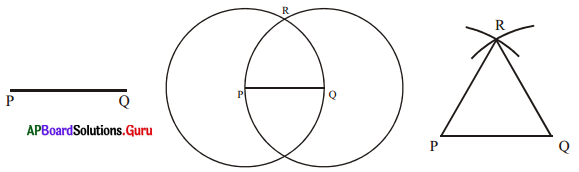
యూక్లిడ్ మూడవ స్వీకృతం భావన నుండి “ఇచ్చిన కేంద్రం, వ్యాసార్ధాలతో వృత్తాన్ని నిర్మించగలం”. కావున P కేంద్రంగా మరియు PQ వ్యాసార్ధం ఒక వృత్తాన్ని గీయండి. అదే విధంగా Q కేంద్రంగా QP వ్యాసార్ధంతో మరొక వృత్తాన్ని గీయండి. ఈ రెండు వృత్తాలు R వద్ద ఖండించుకొంటాయి. ‘R’ ను P మరియు Q లతో కలుపగా Δ PQR ఏర్పడుతుంది.
ఇప్పుడు ఈ విధంగా ఏర్పడిన త్రిభుజం సమబాహు త్రిభుజమని నిరూపించాలి. అంటే PQ = QR = RP అని చూపాలి.
PQ = PR (P కేంద్రంగా గల వృత్త వ్యాసార్ధాలు).
PQ = QR (Q కేంద్రంగా ‘గల వృత్త వ్యాసార్ధాలు)
యూక్లిడ్ సామాన్య భావనల నుండి “ఒకే రాశులకు సమానమైన రాశులు ఒకదానికి మరొకటి సమానాలు” కావున PQ = QR = RP. అందువలన Δ PQR ఒక సమబాహు త్రిభుజం P మరియు Q కేంద్రాలుగా గల వృత్తాలు ఒక బిందువు వద్ద ఖండించుకొంటాయి అనే విషయాన్ని ప్రస్తావించకుండా యూక్లిడ్ తన నిరూపణలో వినియోగించడం గమనించండి.
![]()
3. రెండు వేర్వేరు రేఖలు ఒకటికన్నా ఎక్కువ సంఖ్యలో ఉమ్మడి బిందువులను కలిగియుండవు. (పేజీ నెం. 67)
సాధన.
దత్తాంశం : దత్తరేఖలు l మరియు m.
సారాంశం (నిరూపించవలసినది) : l మరియు m రేఖలకు ఒకే ఒక ఉమ్మడి బిందువు ఉంటుంది.
నిరూపణ : ఆ రెండు రేఖలు రెండు వేర్వేరు బిందువులు A మరియు B వద్ద ఖండించుకొనును అని అనుకొనుము.
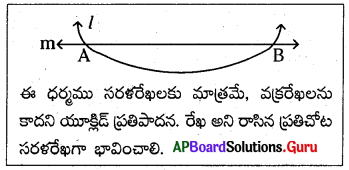
ఇప్పుడు మనకు A మరియు B బిందువుల గుండా పోయే రేఖలు రెండు కలవు. ఇది యూక్లిడ్ స్వీకృతం “రెండు వేర్వేరు బిందువుల గుండా పోయే సరళరేఖ ఒకే ఒకటి ఉంటుంది” కి విరుద్ధంగా ఉంది. ఈ విరుద్ధత “రెండు బిందువుల గుండా రెండు వేర్వేరు రేఖలు కలవు” అని మనం అనుకొన్న ఊహ వలన వచ్చింది. కావున రెండు వేర్వేరు రేఖలు ఒకటి కన్నా మించి ఉమ్మడి బిందువులను కలిగియుండవు.
4. ప్రక్క పటంలో AC = XD; C మరియు D లు AB మరియు XY ల మధ్య బిందువులు. అయిన AB = XY చూపుము. (పేజీ నెం. 67)
సాధన.
AB = 2 AC
(AB మధ్యబిందువు C)
XY = 2 XD
(XY మధ్యబిందువు D)
మరియు AC = XD (దత్తాంశం)
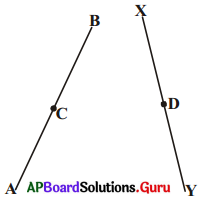
∴ AB = XY
ఎందుకంటే “సమాన రాశుల రెట్టింపులు కూడా సమానమే” – యూక్లిడ్ సామాన్య భావన.