SCERT AP 9th Class Maths Solutions Chapter 3 జ్యామితీయ మూలాలు Ex 3.1 Textbook Exercise Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 3rd Lesson జ్యామితీయ మూలాలు Exercise 3.1
ప్రశ్న1.
కింది వానికి జవాబులు ఇవ్వండి.
i) ఘనాలకు ఎన్ని కొలతలు ఉంటాయి ?
సాధన.
ఘనము త్రిమితీయ ఆకారము కావున దీనికి పొడవు, వెడల్పు మరియు ఎత్తు (లేక) లోతు అను మూడు కొలతలు ఉంటాయి.
ii) “యూక్లిడ్ ఎలిమెంట్స్” అనే గ్రంథంలో ఎన్ని పుస్తకములు ఉన్నాయి ?
సాధన.
“యూక్లిడ్ ఎలిమెంట్స్” అను గ్రంథంలో 13 పుస్తకాలు ఉన్నాయి.
iii) ఘనము మరియు దీర్ఘఘనములకు ఎన్ని తలములు ఉన్నాయి ?
సాధన.
ఘనము మరియు దీర్ఘ ఘనములకు ‘6’ తలాలు ఉండును.
iv) త్రిభుజ అంతర కోణాల మొత్తం ఎంత ?
సాధన.
త్రిభుజ అంతరకోణాల మొత్తము 180°.
v) జ్యామితిలోని మూడు అనిర్వచిత పదాలు రాయండి.
సాధన.
బిందువు, రేఖ మరియు తలము అను పదాలను అనిర్వచిత పదాలంటారు.
![]()
ప్రశ్న2.
కింది ప్రవచనాలు సత్యమో కాదో చెప్పండి. కారణాలు వివరించండి.
a) దత్త బిందువు గుండా పోవు ఒకే ఒక రేఖ ఉంటుంది.
b) అన్ని లంబకోణాలు సమానం.
c) సమాన వ్యాసార్ధాలు గల వృత్తాలు సమానం.
d) రేఖను ఇరువైపులా నిరంతరంగా పొడిగించి ‘రేఖ’ను పొందగలం.
![]()
e) పై పటం 2(d) నుండి AB > AC
సాధన.
a) అసత్యము
b) సత్యము
c) సత్యము
d) సత్యము
e) సత్యము
ప్రశ్న3.
పటం నుండి AH > AB + BC + CD అని చూపండి.

సాధన.
ఇచ్చిన రేఖ \(\overleftrightarrow{\mathrm{AH}}\)
పటము నుండి AB + BC + CD = AD
\(\overline{\mathrm{AD}}\) అనునది \(\overline{\mathrm{AH}}\) లో ఒక భాగము.
యూక్లిడ్ స్వీకృతము ప్రకారము కొంతభాగము అనునది మొత్తము కన్నా చిన్నది.
∴ AH > AD ⇒ AH > AB + BC + CD
ప్రశ్న4.
Q బిందువు P మరియు R బిందువుల మధ్య PQ = QR అగునట్లు ఉంటే PQ = \(\frac {1}{2}\)PR అని నిరూపించుము.
సాధన.

ఇచ్చిన రేఖ PR
PQ = QR
PR మీద Q ఒక బిందువు.
∴ PQ + QR = PR
మరియు PQ + PQ = PR [∵ PQ = QR]
2PQ = PR
∴ PQ = \(\frac {1}{2}\)PR
![]()
ప్రశ్న5.
5.2 సెం.మీ. భుజముగా గల ఒక సమబాహు త్రిభుజాన్ని నిర్మించండి.
సాధన.
సోపానం – 1: AB = 5.2 సెం.మీ. పొడవుతో ఒక రేఖాఖండము గీయుము.
సోపానం – 2: A కేంద్రంగా 5.2 సెం.మీ.లతో ఒక చాపమును గీయుము.
సోపానం – 3: B కేంద్రంగా 5.2 సెం.మీ.లతో మరొక చాపమును గీయుము.
సోపానం – 4: రెండు చాపముల ఖండన బిందువును C గా గుర్తింపుము. ABమరియు AC లను కలుపుము.
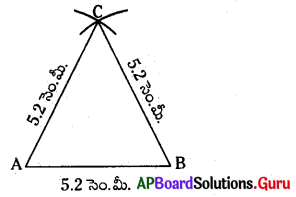
∴ మనకు కావలసిన 5.2 సెం.మీ. భుజంగా గల సమబాహు త్రిభుజము ABC ఏర్పడింది.
ప్రశ్న6.
పరికల్పన అంటే ఏమిటి ? ఒక ఉదాహరణ ఇవ్వండి.
సాధన.
కొన్ని ప్రవచనాలను పరిశీలనల ద్వారా, వివేచనతో సత్యమని భావించి ఊహాత్మకంగా నిర్ణయిస్తాము. ఈ విధముగా సత్యం గానీ, అసత్యం గానీ నిరూపించబడని ప్రవచనాలను పరికల్పనలు అంటారు.
ఉదా : నాలుగు లేక అంతకన్నా పెద్దదైన ప్రతి సరిసంఖ్యను కూడా రెండు ప్రధాన సంఖ్యల మొత్తంగా రాయవచ్చును. దీనిని “గోల్డ్ బాక్ పరికల్పన” అంటారు.
ప్రశ్న7.
P మరియు Q బిందువులను గుర్తించండి. P మరియు Q ల గుండా పోయే రేఖను గీయండి. PQ రేఖకు ఎన్ని సమాంతర రేఖలు గీయగలరు ?
సాధన.
PQ రేఖకు సమాంతరంగా, అనంత రేఖలను గీయగలము.

ప్రశ్న8.
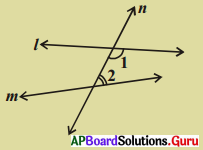
పటంలో రెండు రేఖలు l మరియు m లపై మరొక రేఖ n కలదు. అంతరకోణాలు ∠1 మరియు ∠2ల మొత్తం 180° కన్నా తక్కువ అయిన l మరియు m రేఖల గురించి నీవేమి చెప్పగలవు ?
సాధన.
దత్తాంశము : lమరియు mలు ఏవైనా రెండు రేఖలు. n వాటి యొక్క తిర్యగ్రేఖ.
∠1 మరియు ∠2 ల మొత్తం 180° కన్నా తక్కువ అనగా ∠1 <90° మరియు ∠2 < 90° అగును.
ఈ కోణాల వైపు రేఖలను పొడిగించగా అవి ఖండించుకుంటాయి.
![]()
ప్రశ్న9.
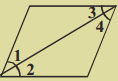
కింది పటంలో ∠1 = ∠3, ∠2 = ∠4 మరియు ∠3 = ∠4 అయిన యూక్లిడ్ సామాన్య భావనలను అనుసరించి ∠1 మరియు ∠2ల మధ్య సంబంధాన్ని రాయండి.
సాధన.
దత్తాంశము : ∠1 = ∠3
∠3 = ∠4
∠2 = ∠4
∠1 = ∠2
∠1 మరియు ∠2 లు, ∠3 మరియు ∠4 లకు సమానము.
(∵ ఒకే రాశులకు సమానమైన రాశులు సమానమను యూక్లిడ్ సామాన్య భావనను అనుసరించి)
ప్రశ్న10.
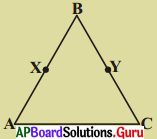
కింది పటములో, BX = \(\frac {1}{2}\) AB, BY = \(\frac {1}{2}\) BC మరియు AB = BC అయిన BX = BY అని చూపండి.
సాధన.
దత్తాంశము :
BX = \(\frac {1}{2}\)AB
BY = \(\frac {1}{2}\)BC
AB = BC
సారాంశము :
BX = BY
ఉపపత్తి : AB = BC [∵ యూక్లిడ్ స్వీకృతము]
\(\frac {1}{2}\)AB = \(\frac {1}{2}\)BC [యూక్లిడ్ భావన అయిన సమాన రాశులలో సగాలు సమానం]
BX = BY