AP SCERT 9th Class Maths Textbook Solutions Chapter 15 గణితములో నిరూపణలు Ex 15.4 Textbook Exercise Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 15th Lesson గణితములో నిరూపణలు Exercise 15.4
1. కింది వాటిలో ఏవి ప్రవచనములు ? ఏవి ప్రవచనములు కావో ? కారణాలు తెల్పుతూ చెప్పండి.
ప్రశ్న (i)
ఆమె కళ్లు నీలంగా కలవు.
సాధన.
ఇది గణిత ప్రవచనము కాదు.
![]()
ప్రశ్న (ii)
x + 7 = 18
సాధన.
ఇది గణిత ప్రవచనము కాదు. దీని సత్య విలువను కనుగొనుట సాధ్యం కాదు.
ప్రశ్న (iii)
ఈ రోజు ఆదివారము కాదు.
సాధన.
ఇది ప్రవచనము కాదు. ఇది సంబద్ధతా ప్రవచనము.
ప్రశ్న (iv)
x యొక్క అన్ని విలువలకు, x + 0 = x
సాధన.
ఇది ఒక గణిత ప్రవచనము.
ప్రశ్న (v)
ఇప్పుడు సమయం ఎంత ?
సాధన.
ఇది గణిత ప్రవచనము కాదు.
![]()
2. కింది ప్రవచనములను ప్రత్యుదాహరణ ద్వారా అసత్యములని తెలపండి.
ప్రశ్న (i)
ప్రతి దీర్ఘచతురస్రము ఒక చతురస్రము.
సాధన.
దీర్ఘ చతురస్రము మరియు చతురస్రములు సమ కోణాలను కలిగి ఉంటాయి. అవి లంబ కోణాలు కాని భుజాలు సమానంగా ఉండవు.
ప్రశ్న (ii)
ఏవైనా వాస్తవ సంఖ్యలు x, y లకు
\(\sqrt{x^{2}+y^{2}}\) = x + y
సాధన.
x = 3; y = 8 అనుకొనుము.
\(\sqrt{x^{2}+y^{2}}=\sqrt{3^{2}+8^{2}}=\sqrt{9+64}=\sqrt{73}\)
x + y = 3 + 8 = 11
ఇక్కడ \(\sqrt{73}\) ≠ 11
∴ \(\sqrt{x^{2}+y^{2}}\) ≠ x + y
ప్రశ్న (iii)
n ఒక పూర్ణసంఖ్య అయిన 2n2 + 11 ఒక ప్రధానాంకము.
సాధన.
n = 11 అయిన 2n2 + 11 = 2(11)2 + 11
= 11 (2 × 11 + 1) = 11 × (22 + 1)
= 11 × 23 ప్రధాన సంఖ్య కాదు.
![]()
ప్రశ్న (iv)
రెందు త్రిభుజములలో అనురూపకోణాలు సమానమైన, ఆ త్రిభుజములు సర్వసమానములు.
సాధన.
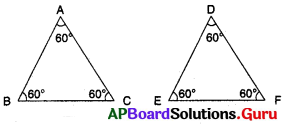
రెండు త్రిభుజాలలో అనురూప కోణాలు సమానమైన, ఆ త్రిభుజాలు సరూపాలు మాత్రమే.
ప్రశ్న (v)
ఒక చతుర్భుజంలోని అన్ని భుజాలు సమానములైన అది చతురస్రము.
సాధన.
ఒక రాంబస్ చతురస్రము కాదు కాని దాని భుజాలు సమానము.
ప్రశ్న 3.
రెండు బేసిసంఖ్యల మొత్తము ఒక సరిసంఖ్య అని నిరూపించండి.
సాధన.
| సోపానాలు | కారణాలు |
| 1. (2m + l), (2n + 1) లు రెండు బేసి సంఖ్యలనుకొనుము.
2. (2m + 1) + (2n + 1) = (2m + 2n + 2) = 2(m + n + 1) = 2k నిరూపించబడినది. |
బేసి సంఖ్యల సాధారణ రూపము
రెండు సంఖ్యలను కలుపగా 2k, k అను సరిసంఖ్యల నిర్వచనము. |
![]()
ప్రశ్న 4.
రెండు సరిసంఖ్యల లబ్దము ఒక సరిసంఖ్య అని నిరూపించండి.
సాధన.
| సోపానాలు | కారణాలు |
| 1. 2m మరియు 2n లు రెండు సరిసంఖ్యలనుకొనుము. 2. 2m . 2n – 4mn = 2 (2mn) = 2K 3. 2K, K = 2mn 4. 2k సరిసంఖ్య నిరూపించబడినది. |
సరిసంఖ్యల సాధారణ రూపము. లభాలను తీసుకొనగాసంఖ్యలను సవరించగా సరిసంఖ్యల నిర్వచనము నుండి |
ప్రశ్న 5.
“x ఒక బేసిసంఖ్య అయిన x2 కూడా ఒక బేసిసంఖ్య” నిరూపించండి.
సాధన.
‘x’ ఒక బేసిసంఖ్య అనుకొనుము.
x = 2m + 1 (బేసిసంఖ్యల సాధారణ రూపము)
x2 = (2m + 1)2 (ఇరువైపులా వర్గం చేయగా)
= 4m2 + 4m + 1
= 2 (2m2 + 2m) + 1
= 2k + 1 {K = 2m2 + 2m}
x2 కూడా ఒక బేసిసంఖ్య
6. కింది వాటిని పరిశీలించండి. వాటిలో ఏది సరియైనది సరిచూడండి.
ప్రశ్న (i)
ఒక సంఖ్యను తలుచుకోండి. దానిని రెట్టింపుచేసి ‘9’ కలపండి. దానికి తలచిన సంఖ్యను కలపండి. 3తో భాగించండి. తిరిగి ‘4’ కలపండి. తిరిగి ఆ ఫలితము నుండి తలచిన సంఖ్యను తీసివేయండి. ఫలితం ‘7’ వచ్చును.
సాధన.
ఒక సంఖ్య = xను ఎన్నుకొనుము.
రెట్టింపు చేయగా = 2x
‘9’ కలుపగా = 2x + 9
తలచిన సంఖ్యను కలుపగా = 2x + 9 + x
= 3x + 9
‘3’ చే భాగించగా = (3x + 9) ÷ 3
= \(\frac{3 x}{3}+\frac{9}{3}\)
= x + 3
తిరిగి ‘4’ కలుపగా = x + 3 + 4
= x + 7
తిరిగి ఫలితం నుండి తలచిన సంఖ్యను తీసివేయగా
= x + 7 – x = 7
∴ ఫలితము = 7 (సత్యము)
![]()
ప్రశ్న (ii)
ఒక 3 – అంకెల సంఖ్యను రాసి, 6 – అంకెల సంఖ్య అగునట్లు, రెండుసార్లు రాయండి. (ఉదా : 425 ను 425425 గా రాయండి) ఈ 6 – అంకెల సంఖ్య (425425) 7, 11 మరియు 13 చే నిశ్శేషముగా భాగింపబడును.
సాధన.
మూడంకెల సంఖ్య xyz అనుకొనుము.
6 – అంకెల సంఖ్య అగునట్లు రెండుసార్లు వ్రాయగా
= xyzxyz
= xyz × (1001)
= xyz × (7 × 11 × 13)
ఈ పరికల్పన సత్యము.