AP Board 9th Class Maths Solutions Chapter 14 సంభావ్యత Ex 14.1

AP SCERT 9th Class Maths Textbook Solutions Chapter 14 సంభావ్యత Ex 14.1 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 14th Lesson సంభావ్యత Exercise 14.1

1. 1-6 అంకెలు ముఖాలుగా గల ఒక పాదికను దొర్లించి, పై ముఖంపై వచ్చిన అంకెను గుర్తించారు. ఇది ఒక యాదృచిక ప్రయోగంగా భావించిన.

ప్రశ్న (a)
సాధ్యమయ్యే పర్యవసానాలు ఏవి ?
సాధన.
సాధ్యమగు పర్యవసానాలు 1, 2, 3, 4,5 మరియు 6

ప్రశ్న (b)
అవి సమసంభవ పర్యవసానాలా ? ఎందుకు ?
సాధన.
అవును, అవి సమ సంభవ పర్యవసానాలు. ఎందుకనగా ప్రతి ఒక్క పర్యవసానము ఏర్పడుటకు సమాన అవకాశం కలదు (లేక) ఏర్పడకపోవుటకు కూడా సమాన అవకాశం కలదు.

ప్రశ్న (c)
పాచిక పై ముఖంపై సంయుక్త సంఖ్య వచ్చే సంభావ్యత ఎంత?
సాధన.
పర్యవసానాలు = 4, 6
మొత్తం పర్యవసానాల సంఖ్య = 2
మొత్తం సాధ్యమయ్యే పర్యవసానాలు = 1, 2, 3, 4, 5 మరియు 6
మొత్తం పర్యవసానాల సంఖ్య = 6
సంభావ్యత = \(\frac {సాధ్యపడు పర్యవసానాల సంఖ్య}{మొత్తం పర్యవసానాల సంఖ్య}\)
= \(\frac{2}{6}=\frac{1}{3}\)

2. ఒక నాణేన్ని 100 సార్లు ఎగురవేసినప్పుడు పర్యవసానాలు కింది విధంగా ఉన్నాయి.
బొమ్మ : 45 సార్లు
బొరుసు : 55 సార్లు అయిన
బొమ్మ = 45 సార్లు
బొరుసు = 56 సార్లు
మొత్తము = 100 సార్లు

ప్రశ్న (a)
ప్రతి పర్యవసానం యొక్క సంభాష్యత కనుక్కోండి.
సాధన.
బొమ్మ పడు సంభావ్యత = P(H) = \(\frac {45}{100}\)
బొరుసు పడే సంభావ్యత = P(T) = \(\frac {55}{100}\)
[∵ సంభావ్యత = \(\frac {సాధ్యపడు పర్యవసానాల సంఖ్య}{మొత్తం పర్యవసానాల సంఖ్య}\)]

ప్రశ్న (b)
ప్రయోగంలో అన్ని పర్యవసానాల సంభావ్యతల మొత్తం కనుక్కోంది.
సాధన.
ప్రయోగంలో అన్ని పర్యవసానాల సంభావ్యతల మొత్తము = P(H) + P(T)
= \(\frac{45}{100}+\frac{55}{100}=\frac{100}{100}\) = 1

3. నాలుగు రంగులు గల ఒక స్పిన్నర్ ను (పటం చూడండి) మన ఒకసారి తిప్పినప్పుడు

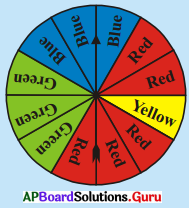
ప్రశ్న (a)
సూచిక ఆగుటకు అధిక అవకాశం గల రంగు ఏది ?
సాధన.
ఎరుపు = 5 సెక్టార్లు
నీలం = 3 సెక్టార్లు
ఆకుపచ్చ = 3 సెక్టార్లు
పసుపు = 1 సెక్టారు
మొత్తము = 5 + 3 + 3 + 1 = 12 సెక్టార్లు
∴ సూచిక ఆగుటకు అధిక అవకాశము గల రంగు ఎరుపు.

ప్రశ్న (b)
సూచిక ఆగుటకు తక్కువ అవకాశం గల రంగు ఏది?
సాధన.
సూచిక ఆగుటకు తక్కువ అవకాశము గల రంగు పసుపు,

ప్రశ్న (c)
సూచిక ఆగుటకు సమాన అవకాశం గల రంగు ఏది?
సాధన.
సూచిక ఆగుటకు సమాన అవకాశము గల రంగులు నీలము మరియు ఆకుపచ్చ. కారణము రెండు రంగులు సమాన సెక్టార్లను కలిగి ఉన్నాయి.

ప్రశ్న (d)
తెలుపు రంగుపై సూచిక ఆగుటకు అవకాశం ఎంత?
సాధన.
తెలుపు రంగుకు సెక్టారు లేదు కావున సూచిక ఆగు అవకాశం లేదు.

ప్రశ్న (e)
సూచిక ఏదైనా రంగుపై కచ్చితంగా ఆగుతుందని చెప్పగలవా ?
సాధన.
చెప్పలేము, ఎందుకనగా ఇది ఒక యాదృచ్ఛిక ప్రయోగము.

4. ఒక సంచిలో ఒక సైజుగల 5 ఆకుపచ్చ రంగు గోళీలు, 3 నీలం రంగు గోళీలు, 2 ఎరుపు రంగు గోళీలు మరియు 2 పసుపు రంగు గోళీలు కలవు. వీటి నుండి యాదృచ్ఛికంగా ఒక గోళీని తీసిన

ప్రశ్న (a)
అన్ని రంగుల పర్యవసానాలు సమ సంభవమా ? వివరించండి.
సాధన.
ఇది సమ సంభవము కాదు. ఎందుకనగా అన్ని రకాల గోళీలు సమాన సంఖ్యలో లేవు.

ప్రశ్న (b)
కింది రంగుల గోళీలు వచ్చు సంభాష్యత కనుక్కోండి. i.e., P(ఆకుపచ్చ), P(నీలం), P (ఎరుపు) మరియు P (పసుపు)
సాధన.
ఆకుపచ్చ గోళీలు = 5
నీలం గోళీలు = 3
ఎరుపు గోళీలు = 2
పసుపు గోళీలు = 2
మొత్తము = 12
సంభావ్యత = \(\frac {అనుకూల పర్యవసానాల సంఖ్య}{మొత్తం పర్యవసానాల సంఖ్య}\)
P(ఆకుపచ్చ) = \(\frac {5}{12}\)
P(నీలం) = \(\frac{3}{12}=\frac{1}{4}\)
P(ఎరుపు) = \(\frac{2}{12}=\frac{1}{6}\)
P(పసుపు) = \(\frac{2}{12}=\frac{1}{6}\)

ప్రశ్న (c)
అన్ని పర్యవసానాల సంభావ్యతల మొత్తం ఎంత ?
సాధన.
P(ఆకుపచ్చ) + P(నీలం) + P(ఎరుపు). + P(పసుపు)
= \(\frac{5}{12}+\frac{3}{12}+\frac{2}{12}+\frac{2}{12}\)
= \(\frac{5+3+2+2}{12}=\frac{12}{12}\) = 1

5. ఆంగ్ల భాషలోని అక్షరాలలో ఒక అక్షరాన్ని యాదృశ్చికంగా ఎన్నుకొనిన, ఆ అక్షరం కింద ఇవ్వబడిన ఘటన అయ్యే సంభావ్యత ఎంత ?
సాధన.
మొత్తం అక్షరాలు = 26 [A, B, C …… Z]
సంభావ్యత = \(\frac {అనుకూల పర్యవసానాల సంఖ్య}{మొత్తం పర్యవసానాల సంఖ్య}\)

ప్రశ్న (a)
ఒక అచ్చు
సాధన.
అచ్చుల సంభావ్యత = \(\frac {5}{26}\)

ప్రశ్న (b)
P అనే అక్షరం తరువాత వచ్చు అక్షరాలు
సాధన.
P తర్వాత వచ్చు అక్షరాలు = 10
[Q, R, S, T, U, V, W, X, Y, Z]
‘P’ తర్వాత వచ్చు అక్షరాల సంభావ్యత = \(\frac{10}{26}=\frac{5}{13}\)

ప్రశ్న (c)
అచ్చు లేదా హల్లు
సాధన.
అచ్చు లేదా హల్లుల సంఖ్య = 26
[A నుండి 2 వరకు అన్ని అక్షరాలు)
అచ్చు లేదా హల్లుల సంభావ్యత = \(\frac {26}{26}\) = 1

ప్రశ్న (d)
అచ్చుకానిది
సాధన.
అచ్చుకానిది = 21
(A, E, I, 0, Uలు తప్ప మిగిలిన అక్షరాలు)
అచ్చుకాని వాటి సంభావ్యత = 2

ప్రశ్న 6.
సంచిపై 5 కిలోలు అని రాయబడిన గోధుమపిండి గల సంచుల అసలు బరువులు కిందినివ్వబడ్డాయి (కి.గ్రా.లలో)
4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, 5.04, 5.07, 5.00
వీటిల్లో యాదృశ్చికంగా ఒక సంచిని తీసినప్పుడు అది 5 కిలోల కంటే ఎక్కువ బరువు ఉండే సంభావ్యత కనుగొనుము.
సాధన.
బస్తాల సగటు = 11
5 కిలోల కంటే ఎక్కువ బరువు గల సంచుల సంఖ్య = 7
[5.05, 5.08, 5.03, 5.06, 5.08, 5.04, 5.07]
∴ సంభావ్యత = \(\frac {అనుకూల పర్యవసానాల సంఖ్య}{మొత్తం పర్యవసానాల సంఖ్య}\)
P(E) = \(\frac {7}{11}\)

7. ఒక పట్టణంలో బీమా సంస్థ 2000 మంది డ్రైవర్లను యాదృచ్చికంగా (ఏ డ్రైవర్‌కు కూడా ప్రత్యేక ప్రాముఖ్యత ఇవ్వకుండా) ఎంపిక చేసింది. వీరి వయసుకు, వీరు చేసిన ప్రమాదాలకు మధ్య ఏదైన సంబంధం అధ్యయనం చేయడం కోసం, కొంత సమాచారం సేకరించింది. ఆ సమాచారం కింది పట్టికలో రాయబడింది.

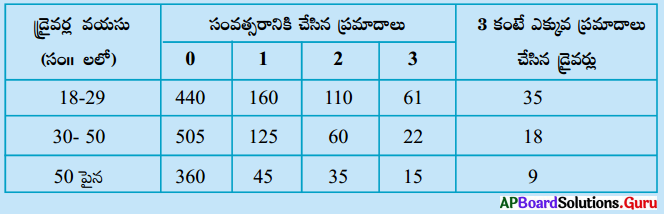
ఒక డ్రైవరును యాదృచ్ఛికంగా ఎంపిక చేసిన

ప్రశ్న (i)
డ్రైవరు 18 – 29 మధ్య వయసు కలిగి ఉండి మూడు ప్రమాదాలు చేసిన సంభావ్యత ఎంత ?
సాధన.
మొత్తం ప్రమాదాల సంఖ్య = 440 + 160 + 110+ 61 + 35 + 505 + 125 + 60 + 22 + 18 + 360 + 45 + 35 + 15 + 9 = 2000
ఘటన : డ్రైవరు (18 – 29) మధ్య వయస్సు కలిగి ఉండి మూడు ప్రమాదాల సంఖ్య = 61
∴ సంభావ్యత P(E) = \(\frac {అనుకూల పర్యవసానాల సంఖ్య}{మొత్తం పర్యవసానాల సంఖ్య}\) = \(\frac {61}{2000}\)

ప్రశ్న (ii)
డ్రైవరు 30-50 మధ్య వయసు కలిగి ఉండి 1 గాని అంతకన్నా ఎక్కువగాని ప్రమాదాలు చేసిన సంభావ్యత
సాధన.
అనుకూల ఫలితాలు = 125 + 60 + 22 + 18 = 225
మొత్తం ప్రమాదాల సంఖ్య = 2000
∴ సంభావ్యత P(E) = \(\frac{1305}{2000}=\frac{261}{400}\)

ప్రశ్న (iii)
డ్రైవరు ప్రమాదాలు చేయని సంభావ్యత
సాధన.
అనుకూల ఫలితాలు = 440 + 505 + 360 = 1305
మొత్తం పర్యవసానాల సంఖ్య = 2000
∴ సంభావ్యత P(E) = \(\frac{1305}{2000}=\frac{261}{400}\)

ప్రశ్న 8.
యాదృచ్ఛికంగా ఒక మొనతేలిన ఐల్లెం (డార్ట్)ను పటంలో చూపిన చతురస్రాకార బోర్డువైపు విసరగా అది షేడి చేసి ప్రాంతంలో తగిలే సంభావ్యత ఎంత ? (x విలువ \(\frac {22}{7}\) తీసుకొని, జవాబును శాతంలో తెల్పండి.)
సాధన.

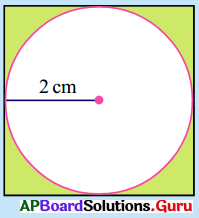
వృత్త వ్యాసార్ధం = r = 2 సెం.మీ.
వృత్త వైశాల్యం = A = πr² = \(\frac {22}{7}\) × 2 × 2 = \(\frac {88}{7}\) సెం.మీ².
చతురస్ర భుజము = 2 × వ్యాసార్థం
= 2 × 2 = 4 సెం.మీ.
చతురస్ర వైశాల్యం = s²
= 4 × 4 = 16 సెం.మీ².
∴ షేక్ చేసిన ప్రాంత వైశాల్యం = చతురస్ర వైశాల్యం – వృత్త వైశాల్యం
= 16 – \(\frac{88}{7}=\frac{112-88}{7}=\frac{24}{7}\)
∴ షేడ్ చేసిన ప్రాంతంలో తగిలే సంభావ్యత = \(\frac {అనుకూల ప్రాంతపు వైశాల్యం}{ మొత్తం వైశాల్యం}\)
P(E) = \(\frac{\frac{24}{7}}{16}=\frac{24}{7 \times 16}=\frac{3}{14}\)
∴ సంభావ్యత శాతములో = \(\frac {3}{14}\) × 100% = \(\frac {300%}{14}\) = 21.428%