AP State Syllabus AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions InText Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 13th Lesson Geometrical Constructions InText Questions
![]()
Try These
Question
Observe the sides, angles and diagonals of quadrilateral BEFD. Name the figures given below and write properties of figures. [Page No. 283]

Solution:
In fig. (1)
\(\overrightarrow{\mathrm{BF}}\) is the bisector of ∠B and ∠F.
In quad BEFD
BE = BD = DF = EF
It is a rhombus
In fig. (2)
BD = BE
FD = FE
∴ BEFD is a kite.
BF is bisector of ∠B and ∠F.
![]()
Try This
Question
Draw a circle, identify a point on it. Cut arcs on the circle with the length of the radius in succession. How many parts can the circle be divided into ? Give reasons. [Page No. 284]
Solution:
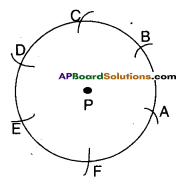
Let P be the centre of the circle.
A is any point on its circumference.
It can be divided into 2π parts
∴ \(\frac{\text { Circumference }}{\text { Radius }}=\frac{2 \pi r}{r}=2 \pi\)
![]()
Think, Discuss and Write
Question
Can you construct a triangle ABC with BC = 6 cm, ∠B = 60° and AB + AC = 5 cm? If , not, give reasons. (Page No. 286)
Solution:
We can’t construct a triangle with measures ∠B = 60°; BC = 6 cm and AB + AC = 5 cm.
∵ AB + AC < BC
Sum of any two sides of a triangle must be greater than the third side.
![]()
Think, Discuss and Write
Question
Can you construct the triangle ABC with the same measures by changing the base angle ∠C instead of ∠B ? Draw a rough sketch and construct it.
BC = 4.2cm. ∠C = 30°, AB – AC = 1.6 cm (Page No. 287)
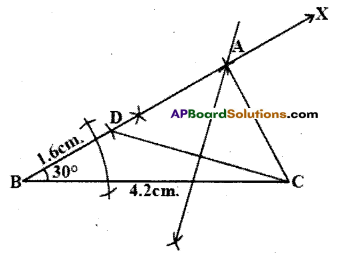
Solution:
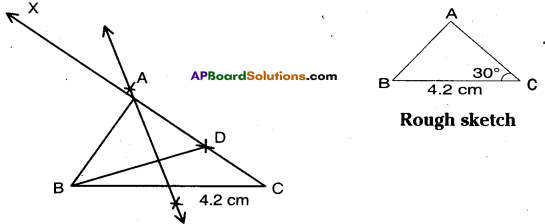
Steps of construction:
- Construct ΔBCD where BC = 4.2 cm and ∠C = 30° and AC – AB = 1.6 cm.
- Draw perpendicular bisector of BD which meets \(\overline{\mathrm{CD}}\) produced at A.
- Join B, D.
- ΔABC is the required triangle.
![]()
Try These
Can you draw the triangle with the same measurements as shown in the figure in alternate way ? (Page No. 289)
[Measurements : ∠B = 6Q°, ∠C = 45° and AB + BC + CA =11 cm]
[Hint: Take ∠YXL = 60°/2 = 30° and ∠XYM = 45°/2 = 22 \(\frac { 1 }{ 2 }\) ]

Solution:
→ Draw XY = 11 cm [AB + BC + CA = 11 cm]
Construct ∠YXP = 30° at X \(\left[\frac{B}{2}=\frac{60^{\circ}}{2}=30^{\circ}\right]\)
Construct ∠XYQ = 22\(\frac { 1 }{ 2 }\) at Y \(\left[\frac{\mathrm{C}}{2}=\frac{45^{\circ}}{2}=22 \frac{1}{2}^{\circ}\right]\)
→ \(\overrightarrow{\mathrm{XP}}\) and \(\overrightarrow{\mathrm{YQ}}\) meet at A.
→ At A, draw \(\overrightarrow{\mathrm{AB}}\) such that ∠XAB = 30° where B is a point on XY.
→ Also draw \(\overrightarrow{\mathrm{AC}}\) such that ∠YAC = 22\(\frac{1}{2}^{\circ}\) where C is a point on XY.
→ Δ ABC is the required triangle.
![]()
Try These
Question
What happens if the angle in the. circle segment is right angle ? What kind of segment do you obtain ? Draw the figure and give reason. [Page No. 290]
Solution:
If the angle in the circle segment is right angle i.e., 90°, then the angle subtended by it at the centre is 2 x 90° = 180°
Thus the line segment becomes the diameter and the circle segment becomes the semi-circle.