AP SCERT 9th Class Maths Textbook Solutions Chapter 13 జ్యామితీయ నిర్మాణాలు Ex 13.2 Textbook Exercise Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 13th Lesson జ్యామితీయ నిర్మాణాలు Exercise 13.2
ప్రశ్న 1.
BC = 7 సెం.మీ., \(\angle \mathbf{B}\) = 75° మరియు AB + AC = 12 సెం.మీ.లతో ∆ABC నిర్మించండి.
సాధన.
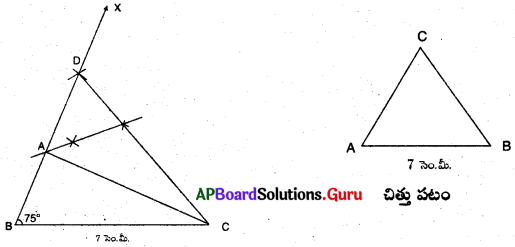
నిర్మాణ సోపానాలు :
→ BC = 7 సెం.మీ.లుగా ఒక రేఖాఖండంను గీయుము.
→ \(\angle \mathrm{B}\) = 75° లతో \(\overrightarrow{\mathrm{BX}}\) కిరణాన్ని నిర్మించండి.
→ \(\overrightarrow{\mathrm{BX}}\) పై BD = AB + AC అగునట్లుగా D బిందువును గీయుము.
→ D, C లను కలుపుము మరియు \(\overline{\mathrm{CD}}\) కు లంబసమద్విఖండన రేఖను గీయగా అది BD ను A వద్ద ఖండించును.
→ A, C లను కలుపగా మనకు కావలసిన ∆ABC ఏర్పడినది.
![]()
ప్రశ్న 2.
QR = 8 సెం.మీ., \(\angle \mathrm{Q}\) = 60° మరియు PQ – PR= 3.5 సెం.మీ. లతో ∆PQR నిర్మించండి.
సాధన.
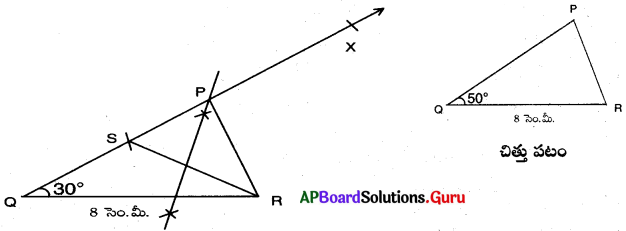
నిర్మాణ సోపానాలు :
→ QR = 8 సెం.మీ.లతో ఒక రేఖాఖండమును గీయుము.
→ \(\angle \mathrm{RQX}\) = 30° అగునట్లుగా Q వద్ద నుండి \(\overrightarrow{\mathrm{QX}}\) ను గీయుము.
→ \(\overrightarrow{\mathrm{QX}}\) పై QS = PQ – PR = 3.5 సెం.మీ. అగునట్లుగా S బిందువును గుర్తించుము. → S, Rలను కలుపుము.
→ \(\overline{\mathrm{QR}}\) కు లంబసమద్విఖండనరేఖను గీయగా అది, \(\overrightarrow{\mathrm{QX}}\) ను ‘P’ వద్ద ఖండించును.
→ P, Rలను కలుపగా ∆PQR ఏర్పడింది.
ప్రశ్న 3.
\(\angle \mathbf{Y}\) = 30°, \(\angle \mathbf{Z}\) = 60° మరియు XY + YZ + ZX = 10 సెం.మీ.లతో ∆XYZ నిర్మించండి.
సాధన.
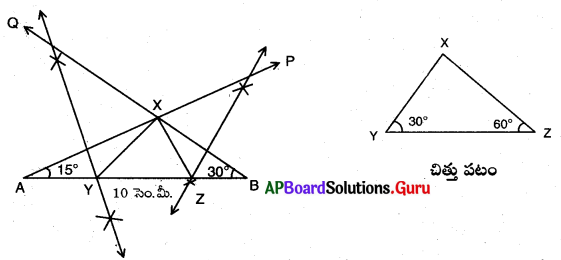
నిర్మాణ సోపానాలు:
→ AB = XY + YZ+ZX = 10 సెం.మీ. లతో ఒక రేఖాఖండంను గీయుము.
→ A వద్ద \(\angle BAP\) = \(\frac {1}{2}\)\(\angle \mathbf{Y}\) మరియు B వద్ద \(\angle ABQ\) = \(\frac {1}{2}\)\(\angle \mathbf{Z}\) అగునట్లుగా గీయుము. వాటిని కలుపగా అవి B వద్ద కలుసుకొనును.
→ XA మరియు XBలకు లంబసమద్విఖండన రేఖలను గీయగా అవి \(\overline{\mathrm{AB}}\) ను Y మరియు Zల వద్ద ఖండించును.
→ X నుండి Y ను మరియు X నుండి Z ను కలుపగా ∆XYZ ఏర్పడును.
![]()
ప్రశ్న 4.
భూమి 7.5 సెం.మీ. మరియు కర్ణం, మూడవ భుజం కొలతల మొత్తం 15 సెం.మీ.గా గల లంబకోణ త్రిభుజాన్ని నిర్మించండి.
సాధన.
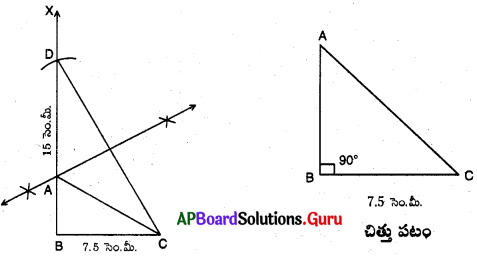
నిర్మాణ సోపానాలు :
→ BC = 7.5 సెం.మీ. లతో ఒక రేఖాఖండాన్ని గీయుము.
→ \(\angle \mathrm{CBX}\) = 90° లను నిర్మించుము.
→ BD = 15 సెం.మీ. లు అగునట్లుగా \(\overrightarrow{\mathrm{BX}}\) పై D ను గుర్తించుము.
→ C, D లను కలుపుము.
→ \(\overline{\mathrm{CD}}\) కు లంబసమద్విఖండనరేఖ గీయగా అది BD ను A వద్ద ఖండించును.
→ A, C లను కలుపగా ∆ABC ఏర్పడును.
5. 5 సెం.మీ. పొడవుగల వృత్త జ్యా తీసుకొని కింది కోణాలను కలిగి ఉండే వృత్తఖండాలను నిర్మించండి.
ప్రశ్న (i)
90°
సాధన.
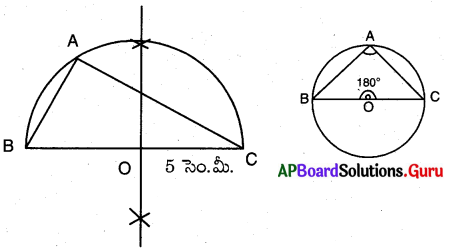
నిర్మాణ సోపానాలు :
→ \(\angle \mathrm{BAC}\) = 90° మరియు \(\angle \mathrm{BOC}\) = 180° లతో ఒక చిత్తు పటంను గీయుము.
→ BC = 5 సెం.మీ.లతో రేఖాఖండమును గీయుము.
→ BC కు లంబసమద్విఖండన రేఖను గీయుము. అది BC ను ఖండించు బిందువు O అగును.
→ OB లేక OC వ్యాసార్థంతో O కేంద్రంగా చాపాలను గీయుము.
→ చాపముపై ఏదైనా బిందువు వద్ద A ను గుర్తించి, B మరియు C లను కలుపుము.
→ \(\angle \mathrm{BAC}\) = 90°
ప్రశ్న (ii)
90°
సాధన.
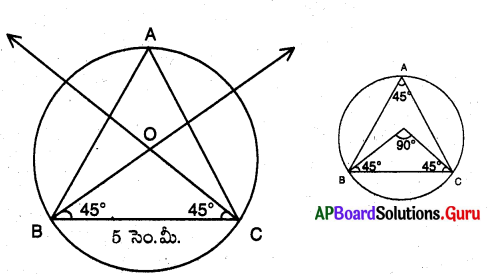
నిర్మాణ సోపానాలు:
→ BC = 5 సెం.మీ. లతో ఒక రేఖాఖండంను గీయుము.
→ BC = 5 సెం.మీ., \(\angle \mathrm{B}\) = 45° = \(\angle \mathrm{C}\) అగునట్లు ∆BOC ను నిర్మించుము.
→ OB లేక OC ను వ్యాసార్ధంతో ‘O’ కేంద్రంగా ఒక వృత్త చాపమును గీయుము,
→ వృత్తఖండంపై A బిందువును గుర్తించి B మరియు C లను కలుపుము.
→ \(\angle \mathrm{BAC}\) = 45°
![]()
ప్రశ్న (iii)
120°
సాధన.
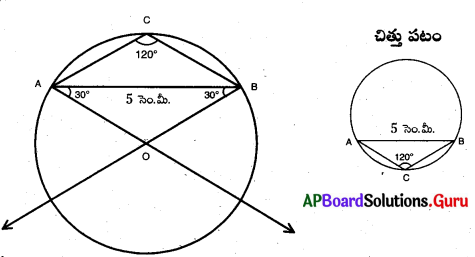
నిర్మాణ సోపానాలు:
→ AB = 5 సెం.మీ.లతో ఒక రేఖాఖండంను గీయుము.
→ \(\angle \mathrm{A}\) = 30°; \(\angle \mathrm{B}\) = 30°; AB = 5 లతో ∆AOB ను గీయుము.
→ ‘O’ కేంద్రముగా ఒక వృత్తఖండంను గీయుము.
→ వృత్తఖండంకు ఎదురుగా C బిందువును గుర్తించి, B మరియు C లను కలుపుము.
→ \(\angle \mathrm{ACB}\) = 120°