AP SCERT 9th Class Maths Textbook Solutions Chapter 12 వృత్తాలు Ex 12.5 Textbook Exercise Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 12th Lesson వృత్తాలు Exercise 12.5
ప్రశ్న 1.
కింది పటాలలో x మరియు y విలువలు కనుక్కోండి.
సాధన.
(i)
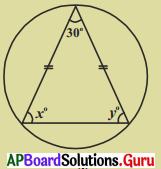
పటం నుండి x = y[∵ సమాన భుజాలకు ఎదురుగల కోణాలు]
కాని x + y + 30° = 180°
∴ x + y = 180° – 30° = 150°
⇒ x = y = \(\frac {150°}{2}\)= 75°
(ii)
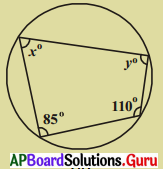
పటం నుండి x° + 110° = 180° [∵ చక్రీయ చతుర్భుజంలో ఎదుటి కోణాలు సంపూరకాలు]
y + 85° = 180
∴ x = 180° – 110°; y = 180° – 85°
x = 70°; y = 95°
(iii)
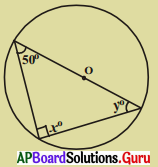
పటం నుండి x = 90° [అర్ధవృత్తంలోని కోణము]
∴ y = 90° – 50° [∵ కోణాల మొత్తం ధర్మం]
= 40°
![]()
ప్రశ్న 2.
ABCD చతుర్భుజంలోని A, B, C లు ఒకే వృత్తంపై ఉన్నాయి. మరియు \(\angle \mathbf{A}+\angle \mathbf{C}\) = 180° అయిన శీర్షం D కూడా అదే వృత్తంపై ఉంటుందని నిరూపించండి.
సాధన.
దత్తాంశము నుండి \(\angle \mathbf{A}+\angle \mathbf{C}\) = 180°
∴ \(\angle \mathbf{B}+\angle \mathbf{D}\) = 360° – 180° = 180°
[∵ చతుర్భుజంలోని కోణాల మొత్తం 360°)
☐ABCD లో, ఎదుటి కోణాల మొత్తము 180°.
∴ ☐ABCD ఒక చక్రీయ చతుర్భుజము.
i.e., A, B మరియు C లు వుండు అదే వృత్తం పైనే D కూడా ఉండును.
ప్రశ్న 3.
ఒక చక్రీయ సమచతుర్భుజం చతురస్రం అవుతుందని నిరూపించండి.
సాధన.
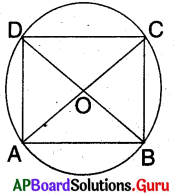
☐ABCD ఒక చక్రీయ సమచతుర్భుజము అనుకొనుము.
అదే విధంగా AB = BC = CD = DA మరియు \(\angle \mathrm{A}+\angle \mathrm{C}=\angle \mathrm{B}+\angle \mathrm{D}\) = 180°
కాని సమచతుర్భుజము ఒక సమాంతర చతుర్భుజము.
∴ ఎదుటి కోణాల జతలు సమానము.
\(\angle \mathrm{A}=\angle \mathrm{C}\) మరియు \(\angle \mathrm{B}=\angle \mathrm{D}\)
∴ \(\angle \mathrm{A}=\angle \mathrm{B}=\angle \mathrm{C}=\angle \mathrm{D}\)
= \(\frac {180°}{2}\) = 90°
∴ ☐ABCD ఒక చతురస్రము.
![]()
ప్రశ్న 4.
కింది వాటిని అన్నింటినీ ఒక వృత్తాన్ని గీచి అందులో అంతర్లిఖించండి. అటువంటి బహుభుజిని నిర్మించలేనిచో ‘సాధ్యం కాదు’ అని రాయండి. జ అని రాయండి.
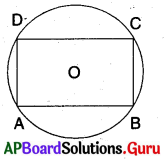
(a) దీర్ఘచతురస్రం
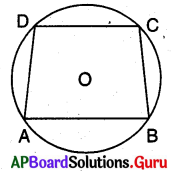
(b) ట్రెపీజియం
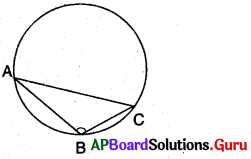
(c) అధిక కోణ త్రిభుజం
(d) దీర్ఘచతురస్రం కాని సమాంతర చతుర్భుజం
(e) అల్పకోణ సమద్విబాహు త్రిభుజం
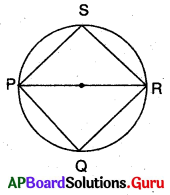
(f) \(\overline{\mathbf{PR}}\) వ్యాసంగా PQRS చతుర్భుజం
సాధన.
(a) దీర్ఘచతురస్రం
(b) ట్రెపీజియం
(c) అధిక కోణ త్రిభుజం
(d) దీర్ఘచతురస్రం కాని సమాంతర చతుర్భుజం (సాధ్యపడదు)
(e) అల్పకోణ సమద్విబాహు త్రిభుజం
(f) \(\overline{\mathbf{PR}}\) వ్యాసంగా PQRS చతుర్భుజం