AP Board 9th Class Maths Solutions Chapter 12 వృత్తాలు Ex 12.4

AP SCERT 9th Class Maths Textbook Solutions Chapter 12 వృత్తాలు Ex 12.4 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 12th Lesson వృత్తాలు Exercise 12.4

ప్రశ్న 1.
పటంలో ‘O’ వృత్తకేంద్రం మరియు \(\angle \mathrm{AOB}\) = 100° అయిన \(\angle \mathrm{ADB}\) ని కనుక్కోండి.

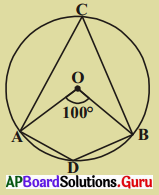
సాధన.

వృత్త కేంద్రము ‘O’
\(\angle \mathrm{AOB}\) = 100°
అదే విధంగా \(\angle \mathrm{ACB}\) = \(\frac {1}{2}\) \(\angle \mathrm{AOB}\)
[∵ ఒక చాపము వృత్తకేంద్రం వద్ద చేయు కోణం, ఆ చాపం మిగిలిన వృత్తంపై ఏ బిందువు వద్ద ఏర్పరచు కోణానికి రెట్టింపు]
= \(\frac {1}{2}\) × 100° = 50°
\(\angle \mathrm{ACB}\) మరియు \(\angle \mathrm{ADB}\) లు సంపూరకాలు.
[∵ చక్రీయ చతుర్భుజంలోని ఎదురెదురు కోణాలు]
∴ \(\angle \mathrm{ADB}\) = 180° – 50° = 130°
(లేక)
అధిక వృత్త చాపము \(\widehat{\mathrm{ACB}}\), D వద్ద ఏర్పరచు కోణము \(\angle \mathrm{ADB}\)
∴ \(\angle \mathrm{ADB}\) = \(\frac {1}{2}\) \(\angle \mathrm{AOB}\) (\(\widehat{\mathrm{ACB}}\) వృత్తకేంద్రం వద్ద ఏర్పరచు కోణము \(\angle \mathrm{AOB}\)
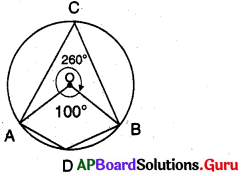
= \(\frac {1}{2}\) [360° – 100°] (పటం నుండి)
= \(\frac {1}{2}\) × 260° = 130°

ప్రశ్న 2.
కింది పటంలో \(\angle \mathrm{BAD}\) = 40° అయిన \(\angle \mathrm{BCD}\)ని కనుగొనండి.

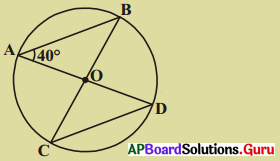
సాధన.
‘O’ వృత్త కేంద్రము
∴ ∆OAB లో OA = OB (వ్యాసార్ధాలు)
∴ \(\angle \mathrm{OAB}\) = \(\angle \mathrm{OBA}\) = 40° (∵ సమాన భుజాలకు ఎదుటి కోణాలు)
\(\angle \mathrm{AOB}\) = 180° – (40° + 40°) (∵ ∆OAB యొక్క కోణాల మొత్తం ధర్మము)
= 180° – 80° = 100°
కాని \(\angle \mathrm{AOB}\) = \(\angle \mathrm{COD}\) = 100°
మరియు \(\angle \mathrm{OCD}\) = \(\angle \mathrm{ODC}\) = 40° [OC = OD]
= 40° ∆OAB లో లాగా
∴ \(\angle \mathrm{BCD}\) = 40°
(లేక)
∆OAB మరియు ∆OCDలలో
OA = OD (వ్యాసార్ధాలు)
OB = OC (వ్యాసార్ధాలు)
\(\angle \mathrm{AOB}\) = \(\angle \mathrm{COD}\) (శీర్షాభిముఖ కోణాలు)
∴ ∆OAB ≅ ∆OCD
∴ \(\angle \mathrm{BCD}\) = \(\angle \mathrm{OBA}\) = 40°
[∵ OB = OA ⇒ \(\angle \mathrm{DAB}\) = \(\angle \mathrm{DBA}\)]

ప్రశ్న 3.
కింది పటంలో ‘O’ వృత్తకేంద్రం మరియు \(\angle \mathrm{PQR}\) = 120° అయిన \(\angle \mathrm{PQR}\) మరియు \(\angle \mathrm{PSR}\) లను కనుగొనండి.

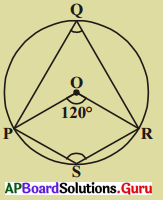
సాధన.
‘O’ వృత్తకేంద్రము మరియు \(\angle \mathrm{PQR}\) = 120°
\(\angle \mathrm{PQR}\) = \(\frac {1}{2}\)\(\angle \mathrm{POR}\) [ [∵ ఒక చాపము వృత్త కేంద్రం వద్ద చేయు కోణం, ఆ చాపము మిగిలిన వృత్తంపై ఏ బిందువు వద్దనైనా ఏర్పరచు కోణంకు రెట్టింపు]
\(\angle \mathrm{PSR}\) = \(\frac {1}{2}\) [\(\widehat{\mathrm{PQR}}\) వృత్తకేంద్రం వద్ద ఏర్పరచ కోణము]
∴ \(\angle \mathrm{PSR}\) = \(\frac {1}{2}\)[360° – 120°] పటం నుండి
= \(\frac {1}{2}\) × 240 = 120°

ప్రశ్న 4.
ఒక సమాంతర చతుర్భుజం చక్రీయమైన, అది దీర్ఘచతురస్రం అవుతుంది. సమర్థించండి.
సాధన.

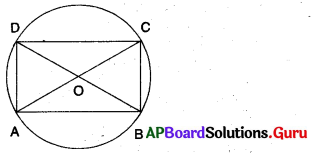
☐ABCD ఒక సమాంతర చతుర్భుజము అనుకొనుము.
A, B, C మరియు Dలు ఒకే వృత్తం పై గల శీర్షాలు.
∴ \(\angle \mathrm{A}+\angle \mathrm{C}\) = 180° మరియు \(\angle \mathrm{B}+\angle \mathrm{D}\) = 180° [∵ చక్రీయ చతుర్భుజములో ఎదుటి కోణాలు సంపూరకాలు]
కానీ \(\angle \mathrm{A}=\angle \mathrm{C}\) మరియు \(\angle \mathrm{B}=\angle \mathrm{D}\)
[∵ ||^gm యొక్క ఎదుటి కోణాలు సమానం]
∴ \(\angle \mathrm{A}=\angle \mathrm{C}=\angle \mathrm{B}=\angle \mathrm{D}\) = \(\frac {180°}{2}\) = 90°
∴ ☐ABCD సమాంతర చతుర్భుజం ఒక దీర్ఘచతురస్రము.

ప్రశ్న 5.
కింది పటంలో ‘O’ వృత్తకేంద్రం OM = 3 సెం.మీ. మరియు AB = 8 సెం.మీ. అయిన వృత్త వ్యాసార్థాన్ని కనుక్కోండి.

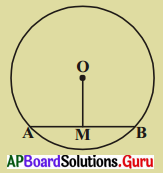
సాధన.

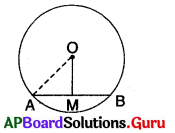
‘O’ వృత్త కేంద్రము.
OM, AB ను సమద్విఖండన చేయును.
∴ AM = \(\frac{\mathrm{AB}}{2}=\frac{8}{2}\) = 4 సెం.మీ.
OA² = OM² + AM²
[∵ పైథాగరస్ సిద్ధాంతం నుండి]
OA = \(\sqrt{3^{2}+4^{2}}\)
= \(\sqrt{9+16}=\sqrt{25}\) = 5 సెం.మీ.

ప్రశ్న 6.
కింది పటంలో ‘O’ వృత్త కేంద్రం మరియు OM, ONలు జ్యాలు PQ, RSలపై కేంద్రం నుండి గీచిన లంబాలు. OM = ON మరియు PQ = 6 సెం.మీ. అయిన RSను కనుక్కోండి.

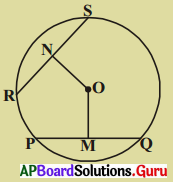
సాధన.
‘O’ వృత్త కేంద్రము.
OM = ON మరియు OM ⊥ PQ; ON ⊥ RS
ఆ విధంగా PQ మరియు RSలు సమానము. [∵ వృత్తకేంద్రము నుండి సమాన దూరంలో గల జ్యాల పొడవులు సమానము]
∴ RS = PQ = 6 సెం.మీ.

ప్రశ్న 7.
A వృత్తకేంద్రం మరియు ABCD ఒక చతురస్రము. BD = 4 సెం.మీ. అయిన వృత్త వ్యాసార్ధం ఎంత ?

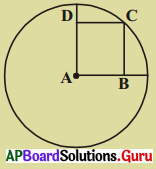
సాధన.

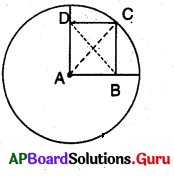
Aవృత్త కేంద్రము మరియు ABCD ఒక చతురస్రము అయిన AC మరియు BD లు కర్ణాలు.
AC = BD = 4 సెం.మీ.
కానీ AC వృత్త వ్యాసార్ధము
∴ వ్యాసార్ధము = 4 సెం.మీ.

ప్రశ్న 8.
ఏదేని వ్యాసార్ధంతో ఒక వృత్తాన్ని గీచి దాని కేంద్రం నుండి సమాన దూరంలో ఉండేట్లు రెండు జ్యాలను గీయండి.
సాధన.

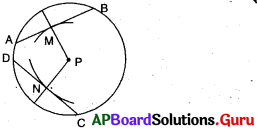
నిర్మాణ సోపానాలు :
→ P కేంద్రంగా ఒక వృత్తంను గీయుము.
→ ఏవైనా రెండు వ్యాసార్ధాలను గీయుము.
→ ఈ వ్యాసార్ధాలపై M మరియు N అను రెండు – బిందువులను గుర్తించుము. అవి PM = PN అగునట్లుగా గుర్తించాలి.
→ M మరియు Nల గుండా వ్యాసార్ధాలను లంబంగా ఉండునట్లు గీయుము.

ప్రశ్న 9.
కింది పటంలో ‘O’ వృత్తకేంద్రం మరియు AB, CDలు సమాన పొడవులు గల జ్యాలు \(\angle \mathbf{AOB}\) = 70° అయిన ∆OCD యొక్క కోణాలను కనుక్కోండి.

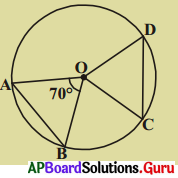
సాధన.
‘O’ వృత్త కేంద్రము
AB, CDలు సమాన జ్యాలు
⇒ సమాన జ్యాలు కేంద్రం వద్ద సమాన కోణాలను ఏర్పరుస్తాయి.
∴ \(\angle \mathrm{AOB}=\angle \mathrm{COD}\) = 70°
∆OCDలో \(\angle \mathrm{OCD}=\angle \mathrm{ODC}\) [∵ OC = OD; సమాన భుజాలకు ఎదుటి కోణాలు]
∴ \(\angle \mathrm{OCD}+\angle \mathrm{ODC}\) + 70° = 180°
⇒ \(\angle \mathrm{OCD}+\angle \mathrm{ODC}\) = 180° – 70° = 110°
∴ \(\angle \mathrm{OCD}+\angle \mathrm{ODC}\) = \(\frac {110°}{2}\) = 55°