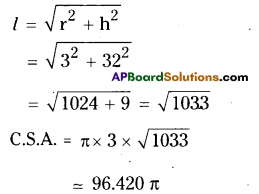AP State Syllabus AP Board 9th Class Maths Solutions Chapter 10 Surface Areas and Volumes Ex 10.3 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 10th Lesson Surface Areas and Volumes Exercise 10.3
![]()
Question 1.
The base area of a cone is 38.5 cm Its volume is 77 cm3. Find its height.
Solution:
Base area of the cone, πr2 = 38.5 cm2
Volume of the cone, V = \(\frac{1}{3}\) πr2 h = 77
πr2 = 38.5
\(\frac{22}{7}\) r2 = 38.5
r2 = 38.5 x \(\frac{7}{22}\)
r2 = 12.25
r = \(\sqrt{12.25}\) = 3.5
V= \(\frac{1}{22}\) x \(\frac{22}{7}\) x 3.5 x 3.5 x h = 77
∴ h = \(\frac{77 \times 3 \times 7}{22 \times 12.25}\) = 6
∴ Height of the cone = 6 cm
Question 2.
The volume of a cone is 462 m3. Its base radius is 7 m. Find its height.
Solution:
The volume of a cone”V’= \(\frac{1}{3}\) πr2 h = 462
Radius ‘r’ = 7 m
Height = h (say)
\(\frac{1}{3}\) x \(\frac{22}{7}\) x 7 x h = 462
h = \(\frac{462 \times 3}{22 \times 7}\) = 9
∴ Height = 9m
![]()
Question 3.
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find (1) radius of the base (ii) total surface area of the cone.
Solution:
C.S.A. of the cone, πrl = 308
Slant height, l = 14 cm
i) πrl = 308; l = 14 cm
\(\frac{22}{7}\) x r x 14 = 308
r = \(\frac{308}{44}\) = 7cm
ii) T.S.A. = πrl + πr2
= πr (r + l) = \(\frac{22}{7}\) x 7 x (7 + 14)
= 22 x 21 = 462 cm3
Question 4.
The cost of painting the total surface area of a cone at 25 paise per cm2 is ₹176. Find the volume of the cone, if its slant height is 25 cm.
Solution:
Slant height of the cone, l = 25 cm
Total cost at the rate of 25 p/cm2
= ₹176
∴ Total surface area of the cone
= \(\frac{176}{25}\) x 100 = 176 x 4 = 704cm2
But T.S.A. of the cone = πr (r + l) = 704
Thus \(\frac{22}{7}\)r(r + 25) = 704
r(r + 25) = \(\frac{704 \times 7}{22}\) = 224
r2 + 25r = 224
⇒ r2 + 32r – 7r – 224 = 0
⇒ r (r + 32) – 7 (r + 32) = 0
⇒ (r + 32) (r – 7) = 0
⇒ r = 7 (∵ ’r’ can’t be negative)
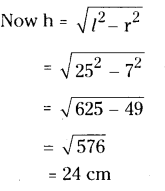
∴ Volume of the cone = \(\frac{1}{3}\) πr2h
= \(\frac{1}{3}\) x \(\frac{22}{7}\) x 7 x 7 24
= 22 x 7 x 8 = 1232cm3
![]()
Question 5.
From a circle of radius 15 cm, a sector with angle 216° is cut out and its bounding radii are bent so as to form a cone. Find its volume.
Solution:
Radius of the sector, ‘r’ = 15 cm
Angle of the sector, ‘x’ = 216°
∴ Length of the arc, l = \(\frac{x}{360}\) x 2πr
\(=\frac{216}{360} 2 \pi r=\frac{3}{5}(2 \pi r)\)
Perimeter of the base of the cone = Length of the arc
2πr of cone = \(=\frac{6}{5}\) πr of the circle
Radius of the cone ‘r’ = \(\frac{3}{5}\) x 15 = 9
Radius ‘r’ of the circle = slant height l of the cone = 9 cm
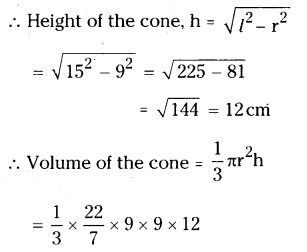
= 1018.3 cm3
![]()
Question 6.
The height of a tent is 9 m. Its base diameter is 24 m. What is its slant height ? Find the cost of canvas cloth required if it costs ₹14 per sq.m.
Solution:
Height of a conical tent ‘h’ = 9 m
Base diameter = 24 m
Thus base radius ’r’= \(\frac{d}{2}=\frac{24}{2}\) = 12m
Cost of canvas = ₹ 14 per sq.m.
C.S.A. of the cone = πrl

![]()
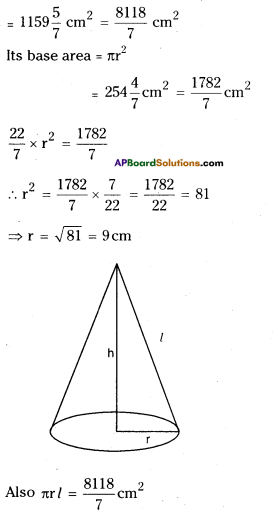
Question 7.
The curved surface area of a cone is 1159\(\frac { 5 }{ 7 }\) cm2. Area of its base is 254 \(\frac { 4 }{ 7 }\) cm2. Find its volume.
Solution:
C.S.A. of the cone = πrl

![]()
Question 8.
A tent is cylindrical to a height of 4.8 m and conical above it. The ra¬dius of the base is 4.5 m and total height of the tent is 10.8 m. Find the canvas required for the tent in square
meters.
Solution:
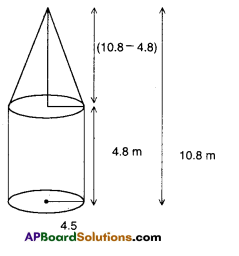
Radius of cylinder, l = 4.5 m
Height of the cylinder = h = 4.8 m
∴ C.S.A. of the cylinder = 2πrh
= 2 x \(\frac{22}{7}\) x 4.5 x 4.8
= 135.771 m2
Radius of the cone ‘r’ =
Radius of the cylinder = 4.5 m
Height of the cone ’h’ = 10.8 – 4.8 = 6 m
∴ Slant height of the cone
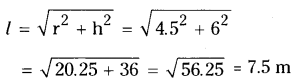
∴ C.S.A. of the cone = πrl
= \(\frac{22}{7}\) x 4.5 x 7.5
= \(\frac{742.5}{7}\) = 106.071m2
∴ Total canvas required
= C.S.A of cylinder + C.S.A. of cone
= 135.771 + 106.071
= 241.842 m2
![]()
Question 9.
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6m? Assume that extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm (use π = 3.14) [Note : Take 20 cm as 0.6 m2]
Solution:
Radius of the cone, r = 6 m
Height of the cone, h = 8 m
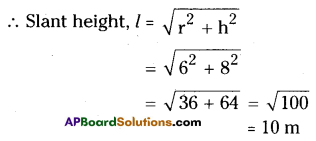
∴ C.S.A. = πrl = 3.14 x 6 x 10 = 188.4 m2
Let the length of the tarpaulin = l
∴ Area of the tarpaulin, lb = 188.4 + 0.6
= 189 m2
⇒ 3l = 189
⇒ l = \(\frac{189}{3}\) = 63m
Question 10.
A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 27 cm. Find the area of the sheet required to make 10 such caps.
Solution:
Radius of the cone, r = 7 cm
Height of the cone, h = 27 cm
Slant height of the cone (l)
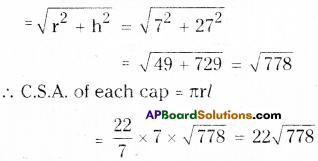
∴ Total area of the sheet required for
10 caps = 10 x 22 \(\sqrt{778}\)
= 6136.383 cm2
![]()
Question 11.
Water is pouring into a conical vessel (as shown in the given figure), at the rate of 1.8 m3 per minute. How long will it take to fill the vessel?

Solution:
From the figure, diameter of the cone 5.2 m
Thus its radius ’r’ = \(\frac{5.2}{2}\) = 2.6 m
∴ Height of the cone = h = 6.8 m
Volume of the cone = \(\frac{1}{3}\) πr2 h
= \(\frac{1}{3} \times \frac{22}{7}\) x 2.6 x 2.6 x 6.8
= \(\frac{1011.296}{21}\)
= 48.156 m3
Quantity of water that flows per minute
= 1.8 m3
∴ Total time required = \(\frac{\text { Total volume }}{1.8}\)
= \(\frac{48.156}{1.8}\) = 26.753
27 minutes.
![]()
Question 12.
Two similar cones have volumes 12π CU. units and 96π CU. units. If the curved surface area of smaller cone is 15π sq.units, what is the curved surface area of the larger one?
Solution:

πrl = 15 π
\(r \sqrt{\left(r^{2}+h^{2}\right)}=15\)
Squaring on both sides
r2 (r2 + h2) = 15 x 15
= 3 x 5 x 3 x 5
= 3 x 3 x 25
r2(r2 + h2) = 32(32 + 42)
∴ r = 3 cm, h = 4 cm
C.S.A. = π x 3 x \(\left(\sqrt{3^{2}+4^{2}}\right)\) = 15π
\(\frac{1}{3}\)πr2H = 96π
\(\frac{3 \times 3 \times \mathrm{H}}{3}\) = 96
∴ H = \(\frac{96}{3}\) = 32 units