AP Board 9th Class Maths Solutions Chapter 1 వాస్తవ సంఖ్యలు Ex 1.4

SCERT AP 9th Class Maths Solutions Chapter 1 వాస్తవ సంఖ్యలు Ex 1.4 Textbook Exercise Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson వాస్తవ సంఖ్యలు Exercise 1.4

ప్రశ్న1.
కింది వానిని సూక్ష్మీకరించండి.
i) (5 + [latex]\sqrt{7}[/latex]) (2 + [latex]\sqrt{5}[/latex])
సాధన.
(5 + [latex]\sqrt{7}[/latex]) (2 + [latex]\sqrt{5}[/latex])
= 10 + 5[latex]\sqrt{5}[/latex] + 2[latex]\sqrt{7}[/latex] + [latex]\sqrt{35}[/latex]

ii) (5+ [latex]\sqrt{5}[/latex]) (5 – [latex]\sqrt{5}[/latex])
సాధన.
(5 + [latex]\sqrt{5}[/latex]) (5 – [latex]\sqrt{5}[/latex]) = (5)² – ([latex]\sqrt{5}[/latex])²
= 25 – 5 = 20

iii) ([latex]\sqrt{3}[/latex] + [latex]\sqrt{7}[/latex])²
సాధన.
([latex]\sqrt{3}[/latex] + [latex]\sqrt{7}[/latex])² = ([latex]\sqrt{3}[/latex])² + ([latex]\sqrt{7}[/latex])² + 2([latex]\sqrt{3}[/latex]) ([latex]\sqrt{7}[/latex])
= 3 + 7 + 2[latex]\sqrt{21}[/latex] = 10 + 2[latex]\sqrt{21}[/latex]

iv) ([latex]\sqrt{11}[/latex] – [latex]\sqrt{7}[/latex])([latex]\sqrt{11}[/latex] + [latex]\sqrt{7}[/latex])
సాధన.
([latex]\sqrt{11}[/latex] – [latex]\sqrt{7}[/latex])([latex]\sqrt{11}[/latex] + [latex]\sqrt{7}[/latex])
= ([latex]\sqrt{11}[/latex])² – ([latex]\sqrt{7}[/latex])²
= 11 – 7 = 4

ప్రశ్న2.
కింది వానిలో అకరణీయ సంఖ్యలేవి? కరణీయ సంఖ్య లేవి?
i) 5 – [latex]\sqrt{3}[/latex]
ii) [latex]\sqrt{3}[/latex] + [latex]\sqrt{2}[/latex]
iii) ([latex]\sqrt{2}[/latex] – 2)²
iv) [latex]\frac{2 \sqrt{7}}{7 \sqrt{7}}[/latex]
v) 2π
vi) [latex]\frac{1}{\sqrt{3}}[/latex]
vii) (2 + [latex]\sqrt{2}[/latex]) (2 – [latex]\sqrt{2}[/latex])
సాధన.
i) 5 – [latex]\sqrt{3}[/latex] – కరణీయ సంఖ్య
ii) [latex]\sqrt{3}[/latex] + [latex]\sqrt{2}[/latex] – కరణీయ సంఖ్య
iii) ([latex]\sqrt{2}[/latex] – 2)² – కరణీయ సంఖ్య
iv) [latex]\frac{2 \sqrt{7}}{7 \sqrt{7}}[/latex] – అకరణీయ సంఖ్య
v) 2π – కరణీయ సంఖ్య కాదు
vi) [latex]\frac{1}{\sqrt{3}}[/latex] – కరణీయ సంఖ్య
vii) (2 + [latex]\sqrt{2}[/latex]) (2 – [latex]\sqrt{2}[/latex]) – అకరణీయ సంఖ్య

ప్రశ్న3.
కింది సమీకరణాలలో x, y, z మొదలగు చరరాశులు అకరణీయ సంఖ్యలను సూచిస్తాయా ? కరణీయ సంఖ్యలను సూచిస్తాయా ?
i) x² = 7
ii) y² = 16
iii) z² = 0.02
iv) u² = [latex]\frac{17}{4}[/latex]
v) w² = 27
vi) t⁴ = 256
సాధన.
i) x² = 7 ⇒ x = [latex]\sqrt{7}[/latex] ఒక కరణీయ సంఖ్య
ii) y² = 16 ⇒ y = [latex]\sqrt{16}[/latex] = 4 ఒక అకరణీయ సంఖ్య
iii) z² = 0.02 ⇒ z = [latex]\sqrt{0.02}[/latex] ఒక కరణీయ సంఖ్య
iv) u² = [latex]\frac{17}{4}[/latex] ⇒ u = [latex]\frac{\sqrt{17}}{2}[/latex] ఒక కరణీయ సంఖ్య
v) w² = 27 ⇒ w = 3[latex]\sqrt{3}[/latex] ఒక కరణీయ సంఖ్య
vi) t⁴ = 256 ⇒ t = [latex]\sqrt[4]{256}=\sqrt[4]{4^{4}}[/latex] = 4 ఒక అకరణీయ సంఖ్య.

ప్రశ్న4.
ఒక వృత్తపరిధికి, దాని వ్యాసానికి గల నిష్పత్తి [latex]\frac{c}{d}[/latex]ని π సూచిస్తాము. మరి π ను కరణీయసంఖ్య అని ఎందుకు పరిగణిస్తారు ?
సాధన.
వృత్తపరిధి (c) మరియు వ్యాసము (d) లు పోల్చదగిన పొడవులు కావు. అనగా ఆ రెంటిని కచ్చితంగా కొలిచే మాపనము లేదు. కాబట్టి π ను కరణీయ సంఖ్యగా పరిగణిస్తాము.

ప్రశ్న5.
హారాలను అకరణీయం చేయండి.
i) [latex]\frac{1}{3+\sqrt{2}}[/latex]
సాధన.

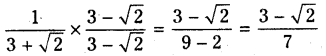
ii) [latex]\frac{1}{\sqrt{7}-\sqrt{6}}[/latex]
సాధన.

iii) [latex]\frac{1}{\sqrt{7}}[/latex]
సాధన.
[latex]\frac{1}{\sqrt{7}}=\frac{1}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}}=\frac{\sqrt{7}}{7}[/latex]

iv) [latex]\frac{\sqrt{6}}{\sqrt{3}-\sqrt{2}}[/latex]
సాధన.

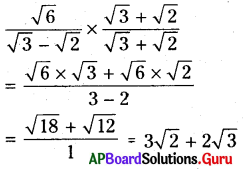
ప్రశ్న6.
హారాలను అకరణీయం చేసి సూక్ష్మీకరించండి.
i) [latex]\frac{6-4 \sqrt{2}}{6+4 \sqrt{2}}[/latex]
సాధన.

ii) [latex]\frac{\sqrt{7}-\sqrt{5}}{\sqrt{7}+\sqrt{5}}[/latex]
సాధన.

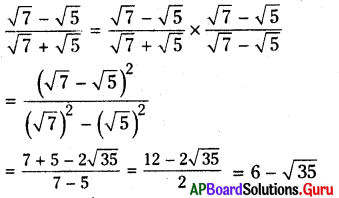
iii) [latex]\frac{3 \sqrt{5}-\sqrt{7}}{3 \sqrt{3}+\sqrt{2}}[/latex]
సాధన.

iv) [latex]\frac{3 \sqrt{5}-\sqrt{7}}{3 \sqrt{3}+\sqrt{2}}[/latex]
సాధన.

ప్రశ్న7.
[latex]\sqrt{2}[/latex] = 1.414, [latex]\sqrt{3}[/latex] = 1.732 మరియు [latex]\sqrt{5}[/latex] = 2.236 అయితే [latex]\frac{\sqrt{10}-\sqrt{15}}{2 \sqrt{2}}[/latex] విలువను మూడు దశాంశ స్థానాల వరకు కనుగొనండి.
సాధన.

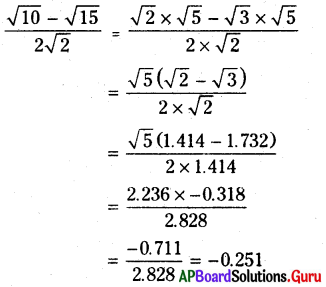
ప్రశ్న8.
విలువలు కనుగొనండి.
i) 64^1/6
సాధన.
64^1/6 = (2⁶)^1/6 = 2

ii) 32^1/5
సాధన.
32^1/5 = (2⁵)^1/5 = 2

iii) 625^1/4
సాధన.
625^1/4 = (5⁴)^1/4 = 5

iv) 16^3/2
సాధన.
16^3/2 = (4²)^3/2 = 4³ = 64

v) 243^2/5
సాధన.
243^2/5 = (3⁵)^2/5 = 3² = 9

vi) (46656)^-1/6
సాధన.
(46656)^-1/6 = (6⁶)^-1/6
= 6^-1 = [latex]\frac{1}{6^{1}}[/latex] = [latex]\frac {1}{6}[/latex]
[∵ 6 × 6 × 6 × 6 × 6 × 6 = 46656]

ప్రశ్న9.
[latex]\sqrt[4]{81}-8 \sqrt[3]{343}+15 \sqrt[5]{32}+\sqrt{225}[/latex] ను సూక్ష్మీకరించండి.
సాధన.

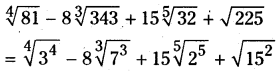
= (3⁴)^1/4 – 8(7³)^1/4 + 15(2⁵)^1/5 + 15
= 3 – 8 × 7 + 15 × 2 + 15
= 3 – 56 + 30 + 15 = -8

ప్రశ్న10.
‘a’ మరియు ‘b’ లు ఏవైనా అకరణీయసంఖ్యలు అయితే కింది సమీకరణాలలో a, b విలువలు కనుక్కోండి.
i) [latex]\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}=a+b \sqrt{6}[/latex]
సాధన.
[latex]\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}[/latex]
హారంను అకరణీయం చేయగా,

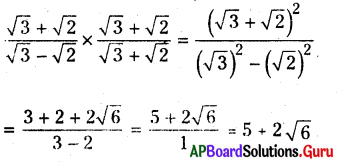
5 + 2[latex]\sqrt{6}[/latex] ను a + b[latex]\sqrt{6}[/latex] తో పోల్చగా
a = 5 మరియు b = 2

ii) [latex]\frac{\sqrt{5}+\sqrt{3}}{2 \sqrt{5}-3 \sqrt{3}}=a-b \sqrt{15}[/latex]
సాధన.
[latex]\frac{\sqrt{5}+\sqrt{3}}{2 \sqrt{5}-3 \sqrt{3}}[/latex]
హారమును అకరణీయం చేయగా,