AP Board 9th Class Maths Solutions Chapter 1 Real Numbers Ex 1.2

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 1 Real Numbers Ex 1.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.2

Question 1.
Classify the following numbers as rational or irrational.
i) \(\sqrt{27}\)
ii) \(\sqrt{441}\)
iii) 30.232342345
iv) 7.484848
v) 11.2132435465
vi) 0.3030030003
Solution:
i) \(\sqrt{27}\) – irrational number
ii) \(\sqrt{441}\) = 21 – rational
iii) 30.232342345 – irrational number
iv) 7.484848 – rational number
v) 11.2132435465 – irrational number
vi) 0.3030030003 – irrational number

Question 2.
Explain with an example how irrational numbers differ from rational numbers ?
Solution:
Irrational numbers can’t be expressed in \(\frac { p }{ q }\) form where p and q are integers and q ≠ 0.
E.g.\(\sqrt{2}, \sqrt{3} ; \sqrt{5}, \sqrt{7}\) etc.
Where as a rational can be expressed in \(\frac { p }{ q }\) form
E.g. :- -3 = \(\frac { -3 }{ 1 }\) and \(\frac { 5 }{ 4 }\) etc.

Question 3.
Find an irrational number between \(\frac { 5 }{ 7 }\) and \(\frac { 7 }{ 9 }\). How many more there may be ?
Solution :
The decimal forms of \(\frac { 5 }{ 7 }\) and \(\frac { 7 }{ 9 }\) are
\(\frac{5}{7}=0 . \overline{714285} \ldots ., \frac{7}{9}=0.7777 \ldots \ldots=0 . \overline{7}\)
∴ An irrational between \(\frac { 5 }{ 7 }\) and \(\frac { 7 }{ 9 }\) is 0.727543…………
There are infinitely many irrational numbers between \(\frac { 5 }{ 7 }\) and \(\frac { 7 }{ 9 }\).

Question 4.
Find two irrational numbers between 0.7 and 0.77.
Solution:
Two irrational numbers between 0.7 and 0.77 can take the form
0.70101100111000111…………. and 0.70200200022……………

Question 5.
Find the value of √5 uPto 3 decimal places.
Solution:

[√5 is not exactly equal to 2.2350679………….. as shown ¡n calculators]

Question 6.
Find the value of √7 upto six decimal places by long division method.
Solution:

Question 7.
Locate \(\sqrt{\mathrm{10}}\) on number line.

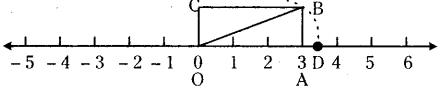
Step – 1 : Draw a number line.
Step – 2 : Draw a rectangle OABC at zero with measures 3 x 1. i.e., length 3 units and breadth 1 unit.
Step – 3 : Draw the diagonal OB.
Step – 4 : Draw an arc with centre ‘O’ and radius OB which cuts the number line at D.
Step – 5 : ‘D’ represents \(\sqrt{\mathrm{10}}[latex] on the number line.

Question 8.
Find atleast two irrational numbers between 2 and 3.
Solution:
An irrational number between a and b is Tab [latex]\sqrt{\mathrm{ab}}\) unless ab is a perfect square.
∴ Irrational number between 2 and 3 is √6

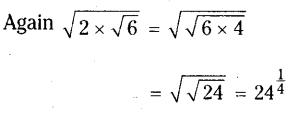
∴ Required irrational numbers are 6^1/2, 24^1/4

Method – II:
Irrational numbers between 2 and 3 are of the form 2.12111231234………….. and 3.13113111311113…….

Question 9.
State whether the following statements are true or false. Justify your answers.
Solution:

1. Every irrational number is a real number – True (since real numbers consist of rational numbers and irrational numbers)
2. Every rational number is a real number – True (same as above)
3. Every rational number need not be a rational number – False (since all rational numbers are real numbers).
4. \(\sqrt{n}\) is not irrational if n is a perfect square – True. (since by definition of an irrational number).
5. \(\sqrt{n}\) is irrational if n is not a perfect square – True. (same as above)
6. All real numbers are irrational – False (since real numbers consist of rational