AP State Syllabus AP Board 8th Class Maths Solutions Chapter 9 Area of Plane Figures Ex 9.1 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 9th Lesson Area of Plane Figures Exercise 9.1
![]()
Question 1.
Divide the given shapes as instructed.
(i)

Solution:
Rectangle ABCD
Rectangle CEFG
Rectangle FHIJ
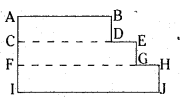
(ii)
Solution:
Rectangle ABCD
Rectangle EFGH
Rectangle CHIJ
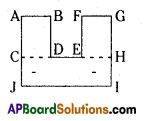
(iii)

Solution:
Trapezium ABEF Trapezium BCDE
(iv)
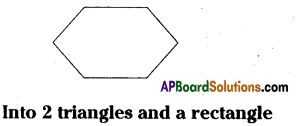
Solution:
Triangle ABC
Triangle DEF B
Rectangle ACDF
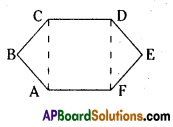
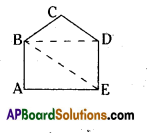
(v)
Solution:
Triangle BCD
Triangle BDE
![]()
Question 2.
Find the area enclosed by each of the following figures
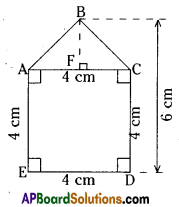
Solution:
i) Area of a pentagon ABCDE = Area of square ACDE + area of Δ ABC
= AE × ED + \(\frac{1}{2}\) AC × BF
= 4 × 4 + \(\frac{1}{2}\) × 4 × 2
[∵ AC = ED = 4 cm;
BF = BD-CD = 6-4 = 2 cm]
= 16 + 4 = 20 sq.cm.
ii)
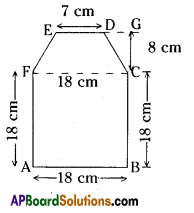
Area of a figure ABCDEF
= Area of square ABCF + area of trapezium CDEF
= AB × BC + \(\frac{1}{2}\) CG × (ED + CF)
= 18 × 18 + \(\frac{1}{2}\) × 8 × (7+ 18)
[∵h = CG = 8 cm, FC = AB = 18 cm]
= 324 + 4 × 25
= 324 + 100
= 424 cm2
iii)
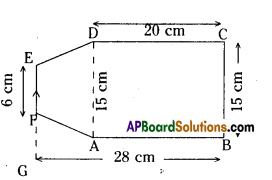
Area of a figure ABCDEF
= Area of rectangle ABCD + area of trapezium ADEF
= AB × BC + \(\frac{1}{2}\) × GA × (EF + AD)
= 20 × 15 + \(\frac{1}{2}\) × 8 × (6 + 15)
[∵ GA = GB-AB = 28-20 = 8cm;
AD = BC – 15 cm]
= 300 + 4 × 21
= 300 + 84
= 384 sq.cm
![]()
Question 3.
Calculate the area of a quadrilateral ABCD when length of the diagonal AC = 10 cm and the lengths of perpendiculars from B and D on AC be 5 cm and 6 cm respectively.
Solution:
From the figire given below
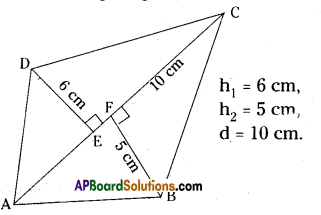
h1 = 6 cm,
h2 = 5 cm,
d = 10 cm.
Area of a quadrilateral ABCD
= \(\frac{1}{2}\) d(h1+h2) . .
= \(\frac{1}{2}\) AC × (DE + BF)
= \(\frac{1}{2}\) × 10(6+5)
= 5 × 11 = 55sq.cm.
Question 4.
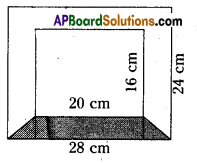
Diagram of the adjacent picture frame has outer dimensions 28 cm × 24 cm and inner dimensions 20 cm × 16 cm. Find the area of shaded part of frame, if width of each section is E the same.
Solution:
The outer dimensions of a picture frame = 28 cm × 24 cm
Length of the outer edge = 28 cm.
Breadth of the outer edge = 24 cm.
Dimensions of inner picture frame = 20 cm × 16 cm
Length of inner edge = 20 cm
Breadth of inner edge = 16 cm.
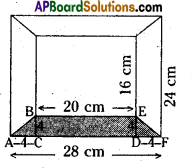
Area of AABC = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × AC × BC
= \(\frac{1}{2}\) × 4 × 4 = 8 cm2
Area of rectangle CDEB = l × b
= CD × DE
= 20 × 4
= 80 cm2
Area of ADEF = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × DF × DE
= \(\frac{1}{2}\) × 4 = 8sq.cm
∴ The area of the shaded region
= ar ΔABC + ar ▭ CDEB + ar ADEF
= 8 + 80 + 8
= 96 sq.cm.
![]()
Question 5.
Find the area of each of the following fields. All dimensions are in metres
Solution:
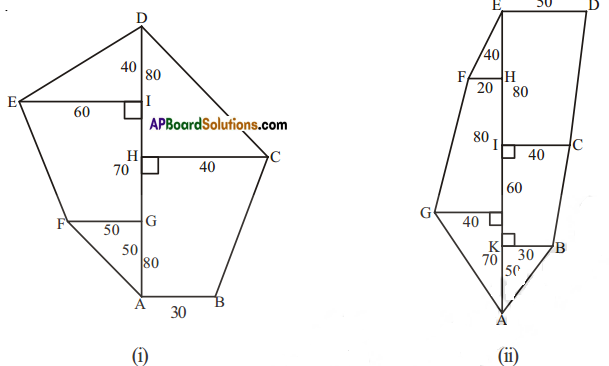
(i) Area of a trapezium ABCH
= \(\frac{1}{2}\) × h(a + b)
= \(\frac{1}{2}\) × 80 × (30 + 40)
= 40 (70)
= 2800 sq.m.
Area of Δ HCD =\(\frac{1}{2}\) × HC × HD
= \(\frac{1}{2}\) × 40 × 80
= 1600 sq.m.
Area of Δ EID = \(\frac{1}{2}\) × El × ID
= \(\frac{1}{2}\) × 60 × 40
= 1200 sq.m.
Area of trapezium FGIE
= \(\frac{1}{2}\) × h(a + b)
= \(\frac{1}{2}\) × 70 × (50 + 60)
= 35 (110)
= 3850 sq.m.
Area of Δ FGA = \(\frac{1}{2}\) × FG × GA
= \(\frac{1}{2}\) × 25 × 50
= 1250 sq.m.
∴ Area of the field
![]()
= 2800 + 1600 + 1200 + 3850 + 1250
= 10700 sq.m.
ii) Area of ΔABK = \(\frac{1}{2}\) × KB × KA
= \(\frac{1}{2}\) x 30 × 50
= 750 sq.m.
Area of trapezium KBCI
= \(\frac{1}{2}\) × h(a + b)
= \(\frac{1}{2}\) × 60 (30 + 40)
= 30 (70)
= 2100 sq.m.
Area of trapezium ICDE
= \(\frac{1}{2}\) × h(a + b)
= \(\frac{1}{2}\) × 80 × (40 + 50)
= 40 (90)
= 3600 sq.m.
Area of Δ FHE = \(\frac{1}{2}\) × FH × HE
=\(\frac{1}{2}\) × 20 × 40
= 400 sq.m.
Area of trapezium GJHF
= \(\frac{1}{2}\) × h(a + b)
= \(\frac{1}{2}\) × 80 × (40 + 20)
= 40 (60)
= 2400 sq.m.
∴ Area of ΔGJA = \(\frac{1}{2}\) × GJ × JA
= \(\frac{1}{2}\) × 40 × 70
= 1400 sq.m.
![]()
∴ Area of the field

= 750 + 2100 + 3600 + 400 + 2400 + 1400
= 10650 sq.m.
Question 6.
The ratio of the length of the parallel sides of a trapezium is 5:3 and the distance between them is 16cm. If the area of the trapezium is 960 cm2, find the length of the parallel sides.
Solution:
The ratio of the length of parallel sides of a trapezium = 5:3.
Let the parallel sides be 5x, 3x say.
∴ a = 5x cm, b = 3x cm
The distance between the parallel sides
(h) = 16 cm.
∴ Area of a trapezium
= \(\frac{1}{2}\) × h(a + b)
= \(\frac{1}{2}\) × 16 x (5x + 3x)
= 8(8x)
= 64 x
According to the problem,
Area of the trapezium = 960 sq.cm.
∴ 64x = 960
x = \(\frac{960}{64}\) = 15
∴ The length of parallel sides
a = 5x = 5 × 15 = 75 cm
b = 3x = 3 × 15 = 45 cm
![]()
Question 7.
The floor of a building consists of around 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of flooring if each tile costs rupees 20 per m2.
Solution:
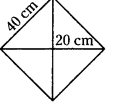
The floor of a building is paved with 3000 tiles.
The shape of each tile is a rhombus.
Diagonals of a tile are
d1 = 45 cm, d2 = 30 cm.
Area of each tile = \(\frac{1}{2}\) × d1 d2
= \(\frac{1}{2}\) × 45 × 30
= 675 sq.cm.
∴ Area of floor
= 3000 × 675
= 2025000 sq.cm
= \(\frac{2025000}{10000}\) sq m
(∵ 1 sq.m. = 10000 sq.cm) 2025
= \(\frac{2025}{10}\) sq.m.
= 202.5 sq.m.
The cost of tile per square meter = ₹ 20
∴ The cost of flooring = ₹ 202.5 × 20
= ₹ 4050
![]()
Question 8.
There is a pentagonal shaped parts as shown in figure. For finding its area Jyothi and Rashida divided it in two different ways. Find the area in both ways and what do you
observe?
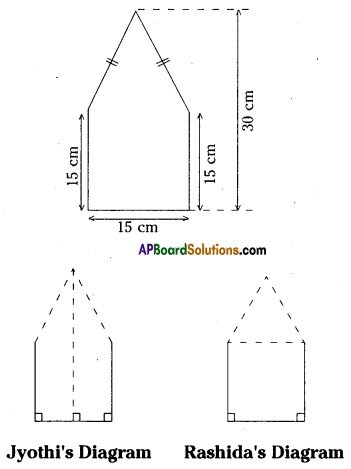
Solution:
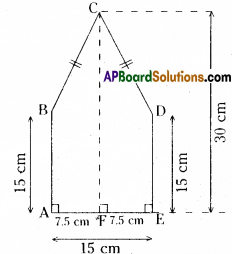
Area of pentagon ABCDE
![]()
= \(\frac{1}{2}\) × AF × (AB + CF) + \(\frac{1}{2}\) FE x (ED + CF)
= \(\frac{1}{2}\) × 7.5 × (15+30) + \(\frac{1}{2}\) x 7.5 x (15+30)
= \(\frac{1}{2}\) × 7.5 × 45 + \(\frac{1}{2}\) x 7.5 x 45
= 2 × (\(\frac{1}{2}\) × 7.5 × 45)
= 7.5 × 45 = 337.50 sq.cm.
Rashida’s Method :
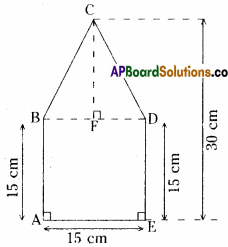
Area of square ABDE = side × side
= AE × ED = 15 × 15 = 225 sq.cm.
Area of ABDC =\(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × BD × CF
= \(\frac{1}{2}\) × 15 × 15
( ∵ CF = 30 – 15 = 15 )
= \(\frac{225}{2}\) = 112.50 sq.cm
∴ Area of pentagon ABCDE
= ar □ ABDE + ar ΔBDC
= 225 + 112.50 = 337.50 sq.cm
The area of a polygon can’t changed if its procedures are changed.