AP Board 8th Class Maths Solutions Chapter 6 Square Roots and Cube Roots Ex 6.5

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 6 Square Roots and Cube Roots Ex 6.5 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 6th Lesson Square Roots and Cube Roots Exercise 6.5

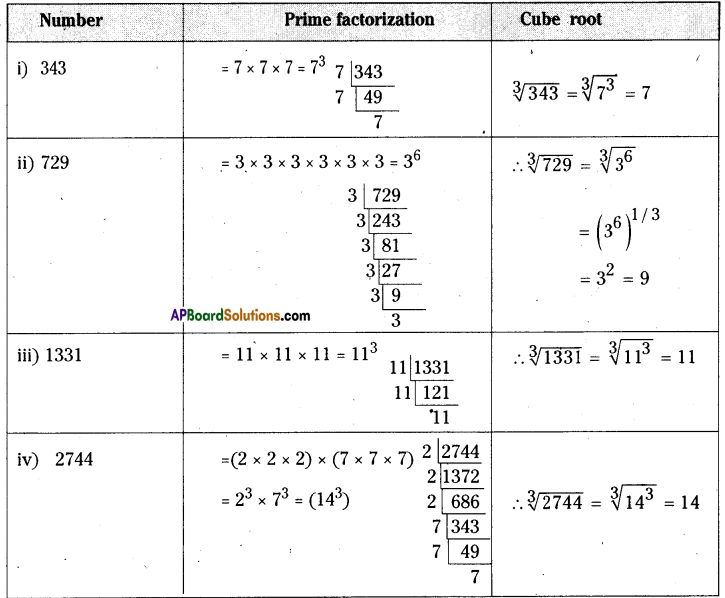
Question 1.
Find the cube root of the following numbers by prime factorization method.
(i) 343
(ii) 729
(iii) 1331
(iv) 2744
Solution:
AP Board 8th Class Maths Solutions Chapter 6 Square Roots and Cube Roots Ex 6.5 1

Question 2.
Find the cube root of the following numbers through estimation’?
(i) 512
(ii) 2197
(iii) 3375
(iv) 5832
Solution:
Step 1: Start making groups of three digits starting from the unit place.
i.e, \(\overline{512}\) First group is 512

Step 2: First group i.e 512 will give us the units digit of the cube root. As 512 ends with 2, then its cube root ends with 8 (2 x 2 x 2) So the units place of the cube root will be 8.

Step 3: Now take the second group i.e. 0. Which is 0³ < 1 < 2³.
So the least number is ‘0′.
∴ Tens digit of a cube root of a number be 0.
∴ \(\sqrt[3]{512}\) = 08 = 8

(ii) 2197
Step 1: Start making groups of three digits starting from the unit place.
AP Board 8th Class Maths Solutions Chapter 6 Square Roots and Cube Roots Ex 6.5 2

Step 2: First group i.e., 197 will give us the units digit of the cube root.
As 197 ends with 7, its cube root ends with 3. ‘
[∵ 3 x 3 x 3 = 27]
∴ Its units digit is 7.

Step 3: Now take the second group i.e.,2
We know that i3 < 2 < 2
∴ The least number be 1.
∴ The required number is 13.
∴ \(\sqrt[3]{2197}=\sqrt[3]{13 \times 13 \times 13}=\sqrt[\not]]{(13)^{8}}\)
= 13

(iii) 3375
Step 1: Start making groups of three digits starting from the unit place.
i.e.;
AP Board 8th Class Maths Solutions Chapter 6 Square Roots and Cube Roots Ex 6.5 3

Step 2: First group is 375. Its units digit is 5.
∴ The cube root is also ends with 5.
∴ The units place of the cube root will be 5.

Step 3: Now take the second group,
i.e., 3 we know that 1³ < 3³ <2³
∴ The least number is 1.
∴ The tens digit of a cube root will be 1.
∴ The required number = 15
\(\sqrt[3]{3375}=\sqrt[3]{15 \times 15 \times 15}=\sqrt[\not]{15^{\not 3}}=15\)

(iv) 5832
Step 1: Start making groups of three digits starting from the unit place.
AP Board 8th Class Maths Solutions Chapter 6 Square Roots and Cube Roots Ex 6.5 4

Step 2: The units digit of 832 is 2.
∴ The cube root of the number ends with units digit 8.
[∵ 8 x 8 x 8 = 512]

Step 3: In the second group i.e., 5 lie between 1 and 6
i.e., 1³ < 5 < 2³
∴ The tens digit of a number will bel.
∴ The required number is 18.
∴ \(\sqrt[3]{5832}=\sqrt[3]{18 \times 18 \times 18}=\sqrt[3]{(18)^{3}}\)
= 18

Question 3.
State true or false?
(i) Cube of an even number is an odd number
(ii) A perfect cube may end with two zeros
(iii) If a number ends with 5, then its cube ends with 5
(iv) Cube of a number ending with zero has three zeros at its right
(v) The cube of a single digit number may be a single digit number.
(vi) There is no perfect cube which ends with 8
(vii) The cube of a two digit number may be a three digit number.
Solution:
(i) Cube of an even number is an odd number (F)
(ii) A perfect cube may end with two zeros (F)
(iii) If a number ends with 5, then its cube ends with 5. (T)
(iv) Cube of a number ending with zero has three zeros at its right. (T)
(v) The cube of a single digit number may be a single digit number. (F)
(vi) There is no perfect cube which ends with 8(F)
(vii) The cube of a two digit number may be a three digit number. (F)

Question 4.
Find the two digit number which is a square number and also a cubic number.
Solution:
The two digited square and cubic
number is 64
∴ 64 = 8 x 8 = 8² ⇒ \(\sqrt{64}\) = 8
64 = 4 x 4 x 4 = 4³ ⇒ \(\sqrt[3]{64}\) = 4