AP Board 7th Class Maths Solutions Chapter 8 ఘాతాంకాలు మరియు ఘాతాలు InText Questions

SCERT AP 7th Class Maths Solutions Pdf Chapter 8 ఘాతాంకాలు మరియు ఘాతాలు InText Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 8th Lesson ఘాతాంకాలు మరియు ఘాతాలు InText Questions

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 56]

ప్రశ్న 1.
కింది వాటిని భూమి 10గా ఉండే విధంగా ఘాతాంక రూపంలో వ్రాయండి.
(i) 10,00,00,000
(ii) 100,00,00,000
సాధన.
(i) 10,00,00,000 = 10⁸
(ii) 100,00,00,000 = 10⁹

అన్వేషిద్దాం [ఆపే నెం. 58]

ప్రశ్న 1.
కింది పట్టికను గమనించి పూరించండి. మొదటిది మీ కోసం చేయబడినది.

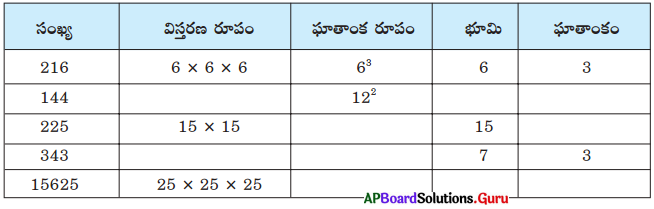
సాధన.

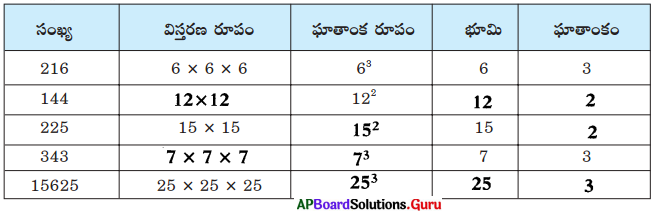
ప్రశ్న 2.
కింది సంఖ్యలను ఘాతాంక రూపంలో రాయండి. వాటి – భూమి, ఘాతాంకం మరియు ఎలా చదువుతారో సూచించండి.
(i) 16
సాధన.
16 = 4² భూమి 4, ఘాతాంకం 2
4 యొక్క 2వ ఘాతం (లేదా)
4 యొక్క వర్గం.
16 = 2⁴ భూమి 2, ఘాతాంకం 4
2 యొక్క 4వ ఘాతం.

(ii) 49
సాధన.
49 = 7² భూమి 7, ఘాతాంకం 2
7 యొక్క 2వ ఘాతం (లేదా)
7 యొక్క వర్గం.

(iii) 512
సాధన.
512 = 2⁹ భూమి 2, ఘాతాంకం 9
2 యొక్క 9వ ఘాతం
512 = 8³ భూమి 8, ఘాతాంకం 3
8 యొక్క 3వ ఘాతం. (లేదా)
8 యొక్క ఘనం.

(iv) 243
సాధన.
243 = 3⁵ భూమి 3, ఘాతాంకం 5 .
3 యొక్క 5వ ఘాతం.

ప్రశ్న 3.
కింది వాటిని గణించి పెద్ద దానిని రాయండి.
(i) 4³ లేదా 3⁴
సాధన.
4³ = 4 × 4 × 4 = 64
3⁴ = 3 × 3 × 3 × 3 = 81
81 > 64 (లేదా) 64 < 81 .
కావున, 3⁴ > 4³, 3⁴ పెద్దది.

(ii) 5³ లేదా 3⁵
సాధన.
5³ = 5 × 5 × 5 = 125
3⁵ = 3 × 3× 3 × 3 × 3 = 243
243 > 125
3⁵ > 5³, 3⁵ పెద్దది.

ప్రశ్న 4.
3² అనేది 2³ కు సమానమా ? మీ జవాబును సమర్ధించండి.
సాధన.
3² = 3 × 3 = 9
2³ = 2 × 2 × 2 = 8
9 ≠ 8 కావున 3² ≠ 2³
∴ 3² అనేది 2³ కు సమానం కాదు.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 60]

ప్రశ్న 1.
కింది సంఖ్యలను ప్రధాన కారణాంక పద్దతిని ఉపయోగించి ఘాత రూపంలో రాయండి.

(i) 432
సాధన.

432 = 2 × 216
= 2 × 2 × 108
= 2 × 2 × 2 × 54
= 2 × 2 × 2 × 2 × 27
= 2 × 2 × 2 × 2 × 3 × 9
= 2 × 2 × 2 × 2 × 3 × 3 × 3
= 24 × 33
∴ 432 = 2⁴ × 3³

(ii) 1296
సాధన.

1296 = 2 × 648
= 2 × 2 × 324
= 2 × 2 × 2 × 162
= 2 × 2 × 2 × 2 × 81
= 2 × 2 × 2 × 2 × 3 × 27
= 2 × 2 × 2 × 2 × 3 × 3 × 9
= 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
= 2⁴ × 3⁴
∴ 1296 = 2⁴ × 3⁴

(iii) 729
సాధన.

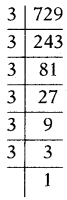
729 = 3 × 243
= 3 × 3 × 81
= 3 × 3 × 3 × 27
= 3 × 3 × 3 × 3 × 9
= 3 × 3 × 3 × 3 × 3 × 3
= 3⁶
∴ 729 = 3⁶

(iv) 1600
సాధన.

1600 = 2 × 800
= 2 × 2 × 400
= 2 × 2 × 2 × 200
= 2 × 2 × 2 × 2 × 100
= 2 × 2 × 2 × 2 × 2 × 50
= 2 × 2 × 2 × 2 × 2 × 2 × 25
= 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5
= 2⁶ × 5²
∴ 1600 = 2⁶ × 5²

అన్వేషిద్దాం. [పేజి నెం. 64]

ప్రశ్న 1.
క్రింది వాటిలో ఖాళీ గడి లో తగిన సంఖ్యను రాయండి.
‘b’ ఏదైనా ఒక శూన్యేతర పూర్ణసంఖ్యగా తీసుకోండి.
(i)

సాధన.

= b² × b³
= b × b × b × b × b = b⁵
∴ b² × b³ = b⁵

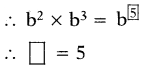
(ii)

సాధన.

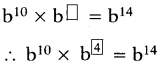
ప్రశ్న 2.
కింది వాటిని a^m × aⁿ = a^{m + n} సూత్రాన్ని ఉపయోగించి సూక్ష్మీకరించండి.
(i) 5⁷ × 5⁴
సాధన.
5⁷ × 5⁴
5⁷ × 5⁴= 5^{7 + 4} = 5¹¹
∴ 5⁷ × 5⁴ = 5¹¹

(ii) p³ × p²
సాధన.
p³ × p²
p³ × p² = p^{3 + 2} = p⁵
∴ p³ × p² = p⁵

(iii) (- 4)¹⁰ × (- 4)³ × (- 4)²
సాధన.
(- 4)¹⁰ × (- 4)³ × (- 4)²
= (- 4)^{10 + 3} × (- 4)²
= (- 4)¹³ × (- 4)²
= (- 4)^{13 + 2}
= (- 4)¹⁵
(లేదా)
= (- 4)^{10 + 3 + 2} = (- 4)¹⁵

అన్వేషిద్దాం [సంకలనం పేజి నెం. 66]

ప్రశ్న 1.
కింది వాటిని (a^m)ⁿ = a^mn సూత్రాన్ని ఉపయోగించి ఘాతరూపంలో రాయండి.
(i) (6²)⁴
సాధన.
(6²)⁴
(6²)⁴ = 6^{2 × 4} = 6⁸ [∵ (a^m)ⁿ = a^mn]
∴ (6²)⁴ = 6⁸

(ii) (2²)¹⁰⁰
సాధన.
(2²)¹⁰⁰
(2²)¹⁰⁰ = 2^{2 × 100} = 2²⁰⁰
∴ (22)100 = 2200

(iii) (20⁶)²
సాధన.
(20⁶)²
(20⁶)² = 20^{6 × 2} = 20¹²
∴ (20⁶)² = 20¹²

(iv) [(- 10)³]⁵
సాధన.
[(- 10)³]⁵
[(- 10)³]⁵ = (- 10)^{3 × 5} = (- 10)¹⁵
∴ [(- 10)³]⁵ = (- 10)¹⁵

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 68]

కింది వాటిని a^m × b^m = (ab)^m న్యాయాన్ని ఉపయోగించి సూక్ష్మీకరించండి.

(i) 7⁶ × 3⁶
సాధన.
7⁶ × 3⁶
7⁶ × 3⁶ = (7 × 3)⁶ = (21)⁶ [∵ a^m × b^m = (ab)^m]
∴ 7⁶ × 3⁶ = 21⁶

(ii) (3 × 5)⁴
సాధన.
(3 × 5)⁴
3⁴ × 5⁴ = (3 × 5)⁴ = 15⁴
∴ (3 × 5)⁴ = 15⁴

(iii) a⁴ × b⁴
సాధన.
a⁴ × b⁴
a⁴ × b⁴ = (a × b)⁴ = (ab)⁴
∴ a⁴ × b⁴ = (ab)⁴

(iv) 3² × a²
సాధన.
3² × a²2
3² × a² = (3 × a)² = (3a)²
∴ 3² × a² = (3a)²

అన్వేషిద్దాం [పేజి నెం. 74]

ప్రశ్న 1.
కింది వాటిని సూక్ష్మీకరించి a^{m – n} లేదా \(\frac{1}{a^{n-m}}\) రూపంలో రాయండి.

(i) \(\frac{10^{8}}{10^{4}}\)
సాధన.
\(\frac{10^{8}}{10^{4}}\) = 10^{8 – 4} = 10⁴ [∵ \(\frac{a^{m}}{a^{n}}\) = a^{m – n}(m > n)]
∴ \(\frac{10^{8}}{10^{4}}\) = 10⁴

(ii) \(\frac{(-7)^{13}}{(-7)^{10}}\)
సాధన.
\(\frac{(-7)^{13}}{(-7)^{10}}\) = (- 7)^{13 – 10}
= (- 7)³ = – 7 × – 7 × – 7 = – 343
∴ \(\frac{(-7)^{13}}{(-7)^{10}}\) = (- 7)³ (లేదా) – 343

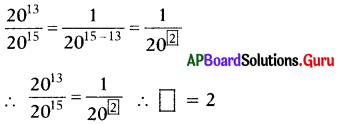
(iii) \(\frac{12^{5}}{12^{8}}\)
సాదన.

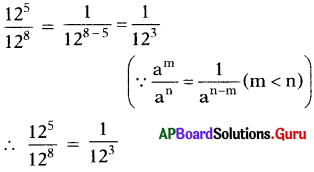
(iv) \(\frac{3^{4}}{3^{7}}\)
సాదన.
\(\frac{3^{4}}{3^{7}}\) = \(\frac{1}{3^{7-4}}\) = \(\frac{1}{3^{3}}\)
∴ \(\frac{3^{4}}{3^{7}}\) = \(\frac{1}{3^{3}}\)

ప్రశ్న 2.
ఖాళీ గడిని సరైన సంఖ్యతో నింపండి.

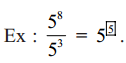
(i)

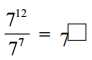
సాధన.

(ii)

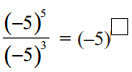
సాధన.

(iii)

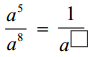
సాధన.

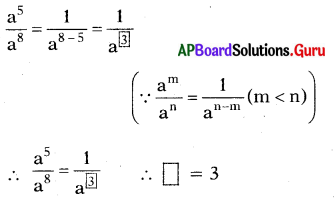
(iv)

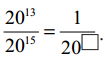
సాధన.

ప్రశ్న 3.
కింది వాటిని సూక్ష్మీకరించండి.
(i) \(\frac{6^{8}}{6^{8}}\)
సాదన.
\(\frac{6^{8}}{6^{8}}\) = 6^{8 – 8} = 6⁰ = 1 (∵ a⁰ = 1)

(ii) \(\frac{\mathbf{t}^{10}}{\mathbf{t}^{10}}\)
సాదన
\(\frac{\mathbf{t}^{10}}{\mathbf{t}^{10}}\) = t^{10 – 10} = t¹⁰ = 1 (∵ a⁰ = 1)

(iii) \(\frac{12^{7}}{12^{7}}\)
సాదన
\(\frac{12^{7}}{12^{7}}\) = 12^{7 – 7} = 12⁰ = 1 (∵ a⁰ = 1)

(iv) \(\frac{p^{5}}{p^{5}}\)
సాదన
\(\frac{p^{5}}{p^{5}}\) = p^{5 – 5} = p⁰ = 1 (∵ a⁰ = 1)

నీ ప్రగతిని సరిచూసుకో మన [పేజి నెం. 76]

ప్రశ్న 1.
క్రింది ఖాళీ గడులను పూరించండి.
(i)

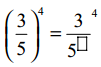
సాధన.

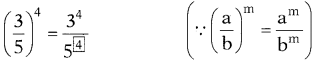
(ii)

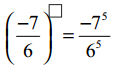
సాధన.

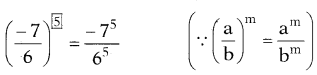
(iii)

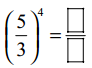
సాధన.

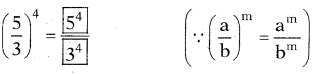
(iv)

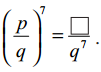
సాధన.

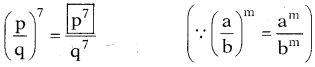
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 78]

ప్రశ్న 1.
కింది వాటిని ఘాత రూపంలో వ్యక్తపరచండి.
(i) \(\frac{-27}{125}\)
షాధన.

(ii) \(\frac{-32}{243}\)
సాధన.

(iii) \(\frac{-125}{1000}\)
సాధన.

(iv) \(\frac{-1}{625}\)
సాధన.

ఆలోచించండి [పేజి నెం. 78]

ప్రశ్న 1.
దీక్షిత మరియు హర్ష 4(3)² ను వేరువేరు విధాలుగా లెక్కించారు. దీక్షిత ఇలా చేసింది.
4(3)2 = (4 × 3)²
= 12²
= 144
హర్ష ఇలా చేశాడు.
4(3)² = 4 × (3 × 3)
= 4 × 9
= 36
ఎవరు సమస్యను తప్పుగా చేశారు ? మీ స్నేహితులతో తప్పు చేయుటకు కారణాలను చర్చించండి.
సాధన.
దీక్షిత తప్పుగా చేసినది.
4(3)² = (4 × 3)² = 12² = 144 గా దీక్షిత తప్పు చేసినది. ఇక్కడ భూమి 3, ఘాతాంకం 2, గుణకం 4.
దీక్షిత గుణకంను కూడా భూమిగా పరిగణించి సమస్యను సాధించింది. కావున తప్పు అయినది.

ఇవి చేయండి కృత్యం [పేజి నెం. 80]

జతను కనుగొనడం: తరగతి గదిని రెండు గ్రూపులుగా విభజించండి. ప్రతి గ్రూపు కూడా కార్డుల కట్టను కలిగి ఉన్నాయి. గ్రూప్-1లోని ప్రతి విద్యార్థి గ్రూపు-2 లోని తగిన విద్యార్థితో జత కూడి సరైన కారణం చెప్పాలి.

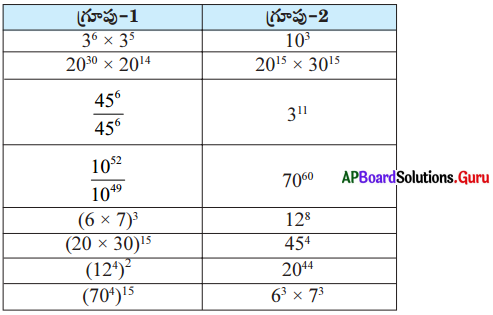
గమనిక: తరగతిలోని విద్యార్థులందరికి ఘాతాంక న్యాయాల పట్ల అవగాహన అయ్యేవరకు ఈ కృత్యాన్ని కొనసాగించవచ్చు.
సాధన.

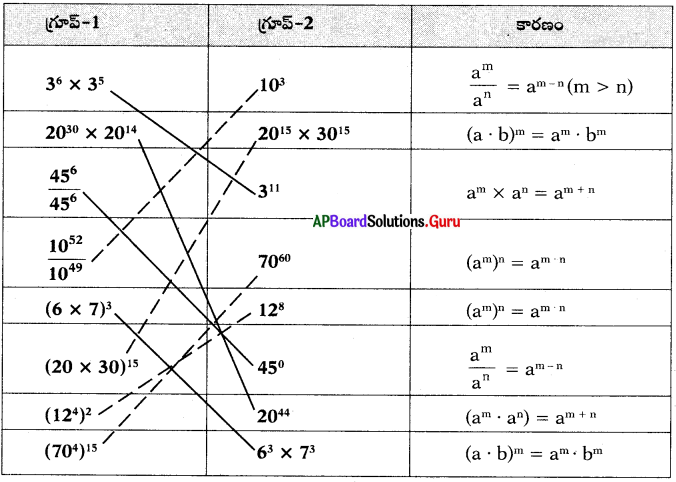
ప్రాజెక్టు పని [పేజి నెం. 84]

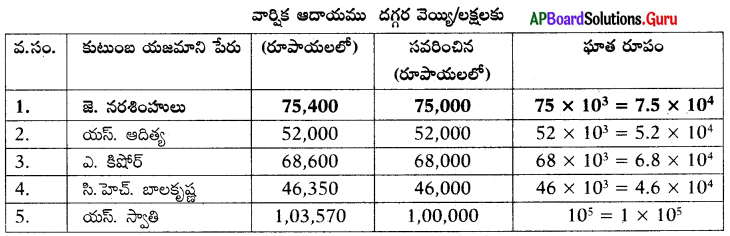
మీ ప్రాంతములోని 5 కుటుంబాల వార్షిక ఆదాయ వివరాలను వారి రేషన్ కార్డును పరిశీలించి దగ్గర వెయ్యి / లక్షలకు సవరించి ఘాత రూపంలో వ్యక్తపరచుము. ఒకటి మీ కోసం చేయబడినవి.

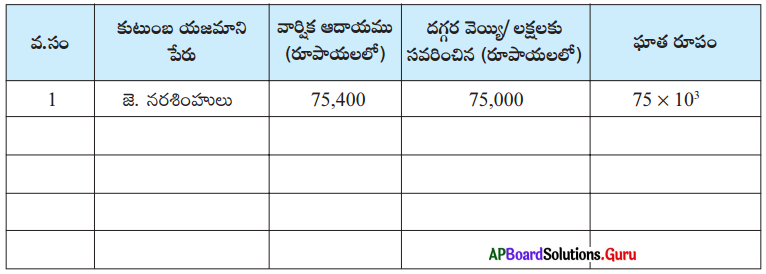
సాధన.

తార్కిక విభాగం

సంఖ్యలలో భిన్నమైన దానిని గుర్తించడం [పేజి నెం. 90]

క్రింద ఇవ్వబడిన ప్రతి ప్రశ్నలో 4 సంఖ్యలు ఇవ్వబడ్డాయి. అందులో 3 ఒకే విధంగా సంబంధాన్ని కలిగి ఉన్నాయి. కాని ఒకటి మాత్రం మిగిలిన మూడు సంఖ్యలకు భిన్నంగా ఉన్నది. మూడింటి మధ్య సంబంధాన్ని కనుగొని భిన్నంగా ఉన్న సంఖ్యను గుర్తించి సమాధానంగా వ్రాయుము.
సంఖ్యలు బేసి / సరి / వరుస సంఖ్యలు, ప్రధాన సంఖ్యలు, ఏదో ఒక సంఖ్య యొక్క గుణిజాలు వర్గాలు లేదా ఘనాలు, కూడిక లేదా తీసివేతలలో ఏదైనా ఒక సంబంధాన్నిగాని విభిన్న సంబంధాల కలయికగానైనా ఉండవచ్చు. ప్రశ్నలు
సమాధానాలు సూచనలు

ప్రశ్న 1.
(a) 12
(b) 25
(c) 37
(d) 49
జవాబు
(c) 37

వివరణ:
ప్రధాన సంఖ్య.

ప్రశ్న 2.
(a) 13
(b) 63
(c) 83
(d) 43
జవాబు
(b) 63

వివరణ:
ప్రధాన సంఖ్య కాదు.

ప్రశ్న 3.
(a) 21
(b) 49
(c) 56
(d) 36
జవాబు
(d) 36

వివరణ:
7 తో భాగింపబడదు.

ప్రశ్న 4.
(a) 112
(b) 256
(c) 118
(d) 214
జవాబు
(b) 256

వివరణ:
వర్గ సంఖ్య.

ప్రశ్న 5.
(a) 42
(b) 21
(c) 84
(d) 35
జవాబు
(d) 35

వివరణ:
3 తో భాగింపబడదు.

ప్రశ్న 6.
(a) 11
(b) 13
(c) 15
(d) 17
జవాబు.
(c) 15

వివరణ:
ప్రధాన సంఖ్య కాదు.

ప్రశ్న 7.
(a) 10
(b) 11
(c) 15
(d) 16
జవాబు
(b) 11

వివరణ:
ప్రధాన సంఖ్య.

ప్రశ్న 8.
(a) 49
(b) 63
(c) 77
(d) 81
జవాబు
(d) 81

వివరణ:
7 తో భాగింపబడదు.

ప్రశ్న 9.
(a) 28
(b) 65
(c) 129
(d) 215
జవాబు
(a) 28

వివరణ:
సరి సంఖ్య.

ప్రశ్న 10.
(a) 51
(b) 144
(c) 64
(d) 121
జవాబు
(a) 51

వివరణ:
వర్గ సంఖ్య కాదు.

ఉదాహరణ

ప్రశ్న 1.
8² లేక 2⁸ లలో ఏది పెద్దది ? సమర్థించండి.
సాధన.
8² = 8 × 8 = 64
2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
256 > 64
∴ 28 > 89.

ప్రశ్న 2.
కింది వాటిని am × an = am + n సూత్రాన్ని ఉపయోగించి సూక్ష్మీకరించండి.
(i) (- 5)⁷ × (- 5)⁴
సాధన.
(- 5)⁷ × (- 5)⁴ = (- 5)^{7 + 4} (∵ a^m × aⁿ = a^{m + n})
= (- 5)¹¹
∴ (- 5)⁷ × (- 5)⁴ = (- 5)¹¹

(ii) 3³ × 3² × 3⁴
సాధన.
3³ × 3² × 3⁴ = 3^{3 + 2 + 4} (∵ a^m × aⁿ = a^{m + n})
= 3⁹
∴ 3³ × 3² × 3⁴ = 3⁹

ప్రశ్న 3.
కింది వాటిని (a^m)ⁿ = a^mn సూత్రాన్ని ఉపయోగించి సూక్ష్మీకరించండి.
(i) (8³)⁴
సాధన.
(8³)⁴ = 8^{3 × 4} [∵ a^m)ⁿ = a^mn
= 8¹²
∴ (8³)^{4</sup = 812}

(ii) [(- 11)⁵]²
సాధన.
[(- 11)⁵]² = (- 11)^{5 × 2}
= (- 11)¹⁰
∴ [(- 11)⁵]² = (- 11)¹⁰

(iii) (7⁵⁰)²
సాధన.
(7⁵⁰)² = 7^{50 × 2}
= 7¹⁰⁰
∴ (7⁵⁰)² = 7¹⁰⁰

ప్రశ్న 4.
కింది వాటిని a^m× b^m = (ab)^m న్యాయాన్ని ఉపయోగించి సూక్ష్మీకరించండి.
(i) 5² × 3²
సాధన.
5² × 3² = (5 × 3)² [∵ a^m × b^m = (ab)^m]

(ii) p³ × q³
సాధన.
p³ × q³ = (p × q)³

(iii) (7 × 8)⁴
సాధన.
(7 × 8)⁴ = 7⁴ × 8⁴ [∵ (ab)^m = a^m × b^m]

ప్రశ్న 5.
కింది వాటిని సూక్ష్మీకరించి \(\frac{a^{m}}{a^{n}}\) = a^{m – n} లేదా \(\) = \(\frac{1}{a^{n-m}}\) రూపంలో రాయండి.

(i) \(\frac{2^{9}}{2^{3}}\)
సాధన.
\(\frac{2^{9}}{2^{3}}\) = 2^{9 – 3} [∵ \(\frac{a^{m}}{a^{n}}\) = a^{m – n}]
= 2⁶

(ii) \(\frac{(-9)^{11}}{(-9)^{7}}\)
సాధన.
\(\frac{(-9)^{11}}{(-9)^{7}}\) = (- 9)^{11 – 7} = (- 9)⁴

(iii) \(\frac{7^{10}}{7^{13}}\)
సాధన.
\(\frac{7^{10}}{7^{13}}\) = \(\frac{1}{7^{13-10}}\) (∵ \(\frac{a^{m}}{a^{n}}\) = \(\left.=\frac{1}{a^{n-m}}\right)\)]
= \(\frac{1}{7^{3}}\)

(iv) \(\frac{6^{2}}{6^{5}}\)
సాధన.
\(\frac{6^{2}}{6^{5}}\) = \(\frac{1}{6^{5-2}}\) = \(\frac{1}{6^{3}}\)

ప్రశ్న 6.
కింది వాటిని \(\frac{a^{m}}{b^{m}}\) = \(\left(\frac{\mathrm{a}}{\mathrm{b}}\right)^{\mathrm{m}}\)సూత్రాన్ని ఉపయోగించి సూక్ష్మీకరించండి.

(i) \(\frac{5^{3}}{2^{3}}\)
సాదన.
\(\frac{5^{3}}{2^{3}}\) = \(\left(\frac{5}{2}\right)^{3}\) (∵ \(\frac{a^{m}}{b^{m}}\) = \(\left(\frac{\mathrm{a}}{\mathrm{b}}\right)^{\mathrm{m}}\))

(ii) \(\left(\frac{8}{5}\right)^{4}\)
సాదన.
\(\left(\frac{8}{5}\right)^{4}=\frac{8^{4}}{5^{4}}\) = \(\frac{8^{4}}{5^{4}}\) (∵ \(\frac{a^{m}}{b^{m}}\) = \(\left(\frac{\mathrm{a}}{\mathrm{b}}\right)^{\mathrm{m}}\))

ప్రశ్న 7.
(1)⁴, (1)⁵, (1)⁷, (- 1)², (- 1)³, (- 1)⁴, (- 1)⁵ విలువలను లెక్కించండి.
సాధన.
(1)⁴ = 1 × 1 × 1 × 1 = 1
(1)⁵ = 1 × 1 × 1 × 1 × 1 = 1
(1)⁷ = 1 × 1 × 1 × 1 × 1 × 1 × 1 = 1
(- 1)² = (- 1) × (- 1) = 1
(- 1)³ = (- 1) × (- 1) × (- 1) = – 1
(- 1)⁴ = (- 1) × (- 1) × (- 1) × (- 1) = 1
(- 1)⁵ = (- 1) × (- 1) × (- 1) × (- 1) × (- 1) = – 1
పై ఉదాహరణల నుండి మనం కింది విషయాలు గమనించవచ్చు.
(i) 1 యొక్క ఏ ఘాతంకైనా దాని విలువ 1.
(ii) (- 1) యొక్క సరి ఘాతం 1 మరియు (- 1) యొక్క బేసి ఘాతం – 1 అగును.
కాబట్టి (- 1)^m = 1 ‘m’ సరిసంఖ్య అయిన
(- 1)^m = – 1 ‘m’ బేసిసంఖ్య అయిన

ప్రశ్న 8.
\(\frac{-8}{27}\) ను ఘాత రూపంలో వ్యక్తపరచండి.
సాధన.
– 8 = (- 2) × (- 2) × (- 2) = (- 2)³
27 = 3 × 3 × 3 = (3)³
∴ \(\frac{-8}{27}\) = \(\frac{(-2)^{3}}{3^{3}}\) = \(\left(\frac{-2}{3}\right)^{3}\)

ప్రశ్న 9.
అభిలాష్ a³ ∙ a² ను a⁶ గా లెక్కించాడు. అతడు చేసినది సరియైనదేనా ?
సాధన.
అభిలాష్ చేసినది సరికాదు. ఎందుకనగా
a³ ∙ a² = a^{3 + 2} = a⁵
[∵ a^m – aⁿ = a^{m + n}]
కావున, a³ ∙ a² = a⁵ అనునది సరియైనది.

ప్రశ్న 10.
రియాజ్ \(\frac{a^{8}}{a^{2}}\) ను a⁴ గా లెక్కించాడు. అతడు చేసినది సరియైనదేనా ? మీ జవాబును సమర్థించండి.
సాధన.
రియాజ్ చేసినది సరికాదు. ఎందుకనగా
\(\frac{a^{8}}{a^{2}}\) = a^{8 – 2} = a⁶ (∵ \(\frac{a^{m}}{a^{n}}\) = a^{m – n}]
∴ \(\frac{a^{8}}{a^{2}}\) = a⁶ అనునది సరియైనది.

ప్రశ్న 11.
కింది వాటిని ప్రామాణిక రూపంలో రాయండి.
(i) 7465
సాధన.
7465 = 7.465 × 1000 (దశాంశం మూడు స్థానాలు ఎడమ వైపుకు మార్చబడుతుంది.)
= 7.465 × 103

(ii) ఎవరెస్ట్ శిఖరం ఎత్తు 8848 మీ.
సాధన.
ఎవరెస్ట్ శిఖరం ఎత్తు = 8848 మీ.
= 8.848 × 1000 మీ. (దశాంశం మూడు స్థానాలు ఎడమ వైపుకు మార్చబడుతుంది.)
= 8.848 × 103 మీ.

(iii) సూర్యుడు మరియు భూమి మధ్య దూరం 149,600,000,000 మీ.
సాధన.
సూర్యుడు మరియు భూమి మధ్య దూరం
= 149,600,000,000 మీ.
= 1.496 × 100000000000 మీ.
= 1.496 × 10¹¹ మీ.

సాధనా ప్రశ్నలు [పేజి నెం. 90]

క్రింద ఇవ్వబడిన వాటిలో భిన్నమైన సంఖ్యను గుర్తించండి.

ప్రశ్న 1.
(a) 3
(b) 9
(c) 5
(d) 7
జవాబు
(b) 9

వివరణ:
3, 5, 7 లు ప్రధాన సంఖ్యలు, 9 సంయుక్త సంఖ్య.

ప్రశ్న 2.
(a) 6450
(b) 1776
(c) 2392
(d) 3815
జవాబు
(d) 3815

వివరణ:
3815 బేసి సంఖ్య, మిగిలినవన్నీ సరిసంఖ్యలు.

ప్రశ్న 3.
(a) 24
(b) 48
(c) 42
(d) 12
జవాబు
(c) 42

వివరణ:
42 తప్ప మిగిలిన అన్ని సంఖ్యలు 12చే భాగింపబడును.

ప్రశ్న 4.
(a) 616
(b) 252
(c) 311
(d) 707
జవాబు
(c) 311

వివరణ:
311 తప్ప మిగిలిన అన్ని సంఖ్యలు పాలిండ్రోమ్ సంఖ్యలు.
(లేదా)
311 తప్ప మిగిలిన అన్ని సంఖ్యలు 7 చే భాగింపడును.

ప్రశ్న 5.
(a) 18
(b) 12
(c) 30
(d) 20
జవాబు
(d) 20

వివరణ:
20 తప్ప మిగిలిన అన్ని సంఖ్యలు 3 చే భాగింపబడుతాయి
(లేదా)
20 తప్ప మిగిలిన అన్ని సంఖ్యలు 6 చే భాగింపబడుతాయి.

ప్రశ్న 6.
(a) 3730
(b) 6820
(c) 5568
(d) 4604
జవాబు
(c) 5568

వివరణ:
ఇచ్చిన సంఖ్యలలో (c) 5568 తప్ప మిగిలిన సంఖ్యలు 3 చే భాగింపబడవు.
(లేదా)
ఇచ్చిన సంఖ్యలలో. (c) 5568 మాత్రమే 6 చే భాగింపబడుతుంది.

ప్రశ్న 7.
(a) 2587
(b) 7628
(c) 8726
(d) 2867
జవాబు
(a) 2587

వివరణ:
(a) 2587 తప్ప మిగిలిన అన్ని సంఖ్యలు 2, 6, 7, 8 అనే అంకెలతో ఏర్పడినవి.
(లేదా)
2587 లో తప్ప మిగిలిన సంఖ్యల అంకమూలం 23 (Digit root).
7628 అంక మొత్తం = 7 + 6 + 2 + 8 = 23 అలాగే,
8726 అంక మొత్తం = 8 + 7 + 2 + 6 = 23
2867 అంక మొత్తం = 2 + 8 + 6 + 7 = 23

ప్రశ్న 8.
(a) 63
(b) 29
(c) 27
(d) 25
జవాబు
(d) 25

వివరణ:
(a) : 25 వర్గ సంఖ్య.

ప్రశ్న 9.
(a) 23
(b) 37
(c) 21
(d) 31
జవాబు
(c) 21

వివరణ:
21 సంయుక్త సంఖ్య, మిగిలిన అన్ని సంఖ్యలు ప్రధాన సంఖ్యలు.

ప్రశ్న 10.
(a) 18
(b) 9
(c) 21
(d) 7
జవాబు
(d) 7

వివరణ:
7 ప్రధాన సంఖ్య, మిగిలిన అన్ని సంఖ్యలు సంయుక్త సంఖ్యలు.
(లేదా)
7 తప్ప మిగిలిన అన్ని సంఖ్యలు ‘3’ చే భాగింప బడతాయి.