SCERT AP 7th Class Maths Solutions Pdf Chapter 7 Ratio and Proportion Review Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 7th Lesson Ratio and Proportion Review Exercise
Question 1.
Find the ratio of the following :
(i) 5,8
Answer:
5 : 8
(ii) ₹ 10, ₹ 15
Answer:
10 : 15
2 : 3
∴ ₹ 10 : ₹15 = 2 : 3
(iii) 25 kg., 20. kg.
Answer:
25 kg : 20 kg
25 : 20
5 : 4
∴ 25 kg : 20 kg = 5 : 4
(iv) 5l, 500ml
Answer:
5l : 500 ml
5000 ml: 500 ml (∵ 1l = 1000 ml, 5l = 5000 ml)
5000 : 500
10 : 1
∴ 5l : 500 ml = 10 : 1
(v) 2 km. 500 m, 1 km. 750 m
Answer:
2 km. 500 m : 1 km. 750 m
2000 m + 500 m : 1000 m + 750 m (∵ 1 km = 1000m; 2 km = 2000 m)
2500 : 1750
10 : 7 (∵ HCF = 25)
∴ 2 km. 500 m : 1 km. 750 m = 10 : 7
(vi) 3 hrs, 1 hr. 30 min.
Answer:
3 hrs : 1 hr. 30 min
3 × 60 : (1 × 60) + 30 (∵ 1 hr = 60 min; 3h = 3 × 60 = 180 min)
180 min : 60 + 30 min
![]()
2 : 1
∴ 3 hrs : 1 hr. 30 min = 2:1
(vii) 40 days, 1 year
Answer:
40 days : 1 year
40 days : 365 days (∵ 1 year = 365 days)
40 : 365 (∵ HCF = 5)
8 : 73
∴ 40 days : 1 year = 8 : 73
(Or)
40 days : 366 days (∵ 1 year = 366 days for leap year)
20 : 183 (∵ HCF = 2)
![]()
Question 2.
Express the following ratios in the simplest form:
(i) 120 : 130
Answer:
Given 120 : 130
![]()
12 : 13
∴ 120 : 130 = 12 : 13
(ii) 135:90
Answer:
Given 135 : 90
27 : 18
3 : 2
∴ 135 : 90 = 3 : 2
(iii) 48 : 144
Answer:
Given 48: 144
12 : 36
1 : 3
∴ 48 : 144 = 1:3
(iv) 81 : 54
Answer:
Given 81 : 54
9 : 6
3 : 2
∴ 81 : 54 = 3 : 2
(v) 432 : 378
Answer:
Given 432 : 378
216 : 189
24 : 21
8 : 7
∴ 432 : 378 = 8 : 7
![]()
Question 3.
Check whether the two ratios given below are in proportion.
(i) 10 : 20, 25 : 50
Answer:
Given 10 : 20, 25 : 50
a :b = 10 : 20
So, a : b = 1 : 2
c : d = 25 : 50
also, c : d = 1 : 2
If a : b = c: d, then a, b, c, d are in proportion.
a : b = c : d = 1 : 2
Therefore, 10 : 20, 25 : 50 are in proportion.
(ii) 18 : 12, 15 : 10
Answer:
Given 18 : 12, 15 : 10
a : b = 18 : 12
= 6 : 4
c : d = 15 : 10
also c : d = 3 : 2
So, a : b = 3 : 2
If a : b = c : d, then a, b, c, d are in proportion.
a : b = c : d = 3 : 2
Therefore, 18 : 12, 15 : 10 are in proportion.
(iii) 25 : 20, 16 : 14
Answer:
Given 25 : 20, 16 : 14
a : b = 25 : 20
So, a : b = 5 : 4
5 : 4 ≠ 8 : 7
∴ a : b ≠ c : d
c : d = 16 : 14
c : d = 8 : 7
If a : b = c : d, then a, b, c, dare in propottion.
Here a : b ≠ c : d
So, a, b, c, d are not in proportion.
(iv) 54 : 27, 18 : 9
Answer:
Given 54 : 27, 18 : 9
a : b = 54 : 27.
= 6 : 3
So, a : b = 2 : 1
c : d = 18 : 9
also, c : d = 2 : 1
If a : b = c : d, then a, b, c, d are in proportion.
a : b = c : d = 2 : 1
Therefore, 54: 27, 18 : 9 are in proportion.
Question 4.
Find the missing number in each of the following problems:
(i) 15 : 19 = 45 : _______
Answer:
Given 15 : 19 = 45 : x
Let the missing term be ‘x’.
If a : b = c : d, then a, b, c and d are in proportion, then the product of extremes is equal to the product of means that is a . d = b . c
⇒ 15 × x = 19 × 45
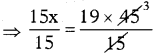
⇒ x = 19 × 3
∴ x = 57
(ii) 9 : 13 = ____ : 65
Answer:
Given 9 : 13 = x : 65
Let the missing term be ‘x’.
If a : b = c : d, then a, b, c and d are in proportion, then the product of extremes is equal to the product of means that is a . d = b . c
⇒ 9 × 65 = 13 × x
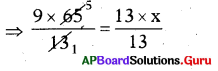
⇒ 45 = x
∴ x = 45
(iii) 8 : ______ = 72 : 63
Answer:
Given 8 : x = 72 : 63
Let the missing term be ‘x’.
If a : b = c : d, then a, b, c and d are in proportion, then the product of extre¬mes is equal to the product of means that is a . d = b . c
⇒ 8 × 63 = x × 72
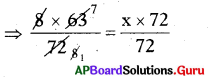
⇒ 7 = x
∴ x = 7
![]()
Question 5.
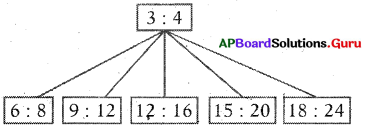
Fill in the boxes with equivalent ratio of 3 : 4.
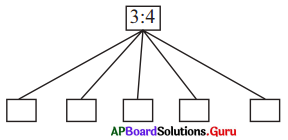
Answer:
Given a : b = 3 : 4 (or) \(\frac{3}{4}\)
\(\frac{a}{b}=\frac{3}{4}\)
Equivalent ratios

Therefore, a : b = 3 : 4 = 6 : 8
= 9 : 12 = 12 : 16 = 15 : 20 = 18 : 24
Question 6.
Pick out any four numbers from below and arrange them so that they are in proportion 2, 3, 10, 12> 15, 18.
Ex : 2 : 10 = 3 : 15
(i) : __________
Answer:
2 : 3; 12 : 18
a : b = 2 : 3, c : d = 12: 18
If a, b, C, d are in proportion, then the product of extremes is equal to the pro¬duct of means.

a . d = b . c
2 × 18 = 3 × 12
36 = 36
So, 2 : 3 = 12 : 18
(ii) : __________
Answer:
10 : 12 = 15 : 18
a : b = 10 : 12
c : d = 15 : 18
If a, b, c, d are in proportion, then the product of extremes is equal to the product of means.

a . d = b . c
10 × 18 = 15 × 12
180 = 180
So, 10 : 12 = 15 : 18
Question 7.
Divide ₹ 1500 into two parts such that they are in the ratio of 7 : 3.
Answer:
Given amount to be divide = ₹ 1500 .
Ratio to be divide = 7:3
Sum of the terms in the ratio = 7 + 3 = 10

[Or 1500 – 1050 = 450]
![]()
Question 8.
If there are 20 chocolates in a packet, Rajani and Ragini share them and Rajani takes 12 chocolates, then what is the ratio of chocolates taken by Rajani to Ragini?
Answer:
Total number of Chocolates = 20
Number of chocolates Rajani taken = 12
Number of chocolates Ragini taken = 20 – 12 = 8
Ratio of Rajani to Ragini = 12 : 8
Ratio of chocolates taken by Rajani to Ragini = 3 : 2
Question 9.
A pipe is cut into two parts in such a ratio that the first part to second part is 7:8. If the length of the 2nd part is 48cm, then what is the length of the first part? What is the total length of the pipe before cutting?
Answer:
Given ratio of two parts of pipe = 7:8
Length of the second part = 48 cm
Length of the first part = x cm
Ratio of the two parts = x : 48

Product of extremes = Product of means
⇒ 8 × x = 48 × 7
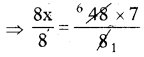
⇒ x = 42
∴ Length of first part of the pipe = x = 42 cm
Length of the pipe = 42 + 48 = 90 cm