SCERT AP 7th Class Maths Solutions Pdf Chapter 7 నిష్పత్తి మరియు అనుపాతం InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 7th Lesson నిష్పత్తి మరియు అనుపాతం InText Questions
[పేజి నెం. 2]
క్రింది చిత్రాలను చూసి ఇచ్చిన ప్రశ్నలకు సమాధానాలను చెప్పండి.
ప్రశ్న1.
చిరుత పులి వేగానికి, మనిషి వేగానికి గల నిష్పత్తి చెప్పగలమా ? ఎంత ?

సాధన :
చిరుతపులి వేగం = 120 కి.మీ./గం.
మనిషి వేగం = 20 కి.మీ./గం.
∴ చిరుత పులి వేగానికి, మనిషి వేగానికి గల నిష్పత్తి
= 120 : 20 = 6:1
![]()
ప్రశ్న2.
హేమ ఎత్తునకు, అమీర్ ఎత్తునకు గల నిష్పత్తి ఎంత ?
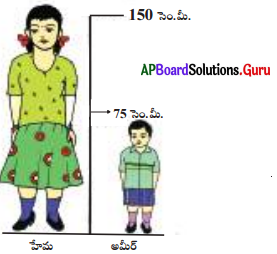
సాధన :
హేమ ఎత్తు = 150 సెం.మీ.
అమీర్ ఎత్తు = 75 సెం.మీ.
∴ ఎత్తుల నిష్పత్తి = 150 : 75 = 2 : 1
ప్రశ్న3.

సాధన :
2 హస్తాల అరటి పండ్ల ధర = ₹ 80
∴ 3 హస్తాల అరటి పండ్ల ధర
= \(\frac{3}{2}\) × 80
= ₹ 120
ప్రశ్న4.
ఏ కారక నిష్పత్తి, కట్టడాలను మరింత అందంగా ఆకర్షణీయంగా తయారు చేస్తుందో మీకు తెలుసా ?
సాధన :
బంగారు నిష్పత్తి మరింత అందంగా, ఆకర్షణీయంగా కట్టడాలను తయారు చేస్తుంది. ఎందుకనగా, అది రెండు వేరు వేరు (కట్టడాల) పొడవులను రెండు రేఖాభాగాలుగా విభజిస్తుంది. మొత్తం నిష్పత్తి పెద్దదైన రేఖాభాగం మరియు చిన్నదానికి కూడా సమానం.
నీ ప్రగతిని సరిచూసుకో [పే నెం.8]
ప్రశ్న1.
క్రింది ఇచ్చిన నిష్పత్తుల బహుళ నిష్పత్తిని కనుగొనండి.
(i) 3 : 5 మరియు 4 : 3
సాధన:
3:5 మరియు 4 : 3 ల బహుళ నిష్పత్తి
![]()
(ii) 8 : 3 మరియు 6:5
సాధన:
8 : 3 మరియు 6 : 5 ల బహుళ నిష్పత్తి
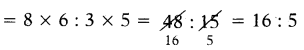
(iii) 2 : 1 మరియు 8 : 7
సాధన :
2 : 1 మరియు 8 : 7 ల బహుళ నిష్పత్తి
2 × 8 : 1 × 7 = 16 : 7
![]()
ప్రశ్న2.
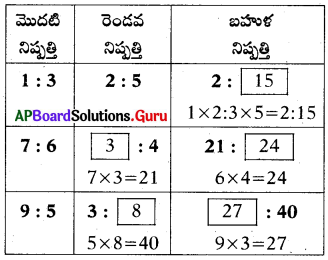
ఈ క్రింది ఖాళీలను సరైన సమాధానాలతో పూరించండి.
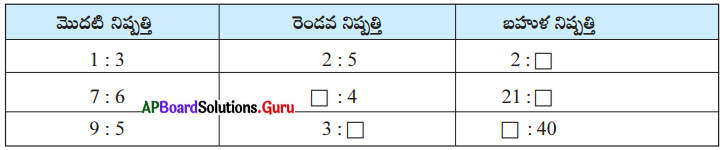
సాధన :
అన్వేషిద్దాం [పేజి నెం. 12]
→ ఒక ఇల్లు కట్టడానికి అవసరమైన కూలి పనివాళ్ళ సంఖ్య, వాళ్ళకి రోజువారి ఇచ్చే మొత్తం వేతనాన్ని క్రింద ఇవ్వబడింది.

సాధన:

ఆలోచించండి [పేజి నెం. 14]
→ 4 నోటు పుస్తకాల వెల ₹ 80 అయిన 7 నోటు పుస్తకాల వెల ఎంత ? పై సమస్యను ఏకవస్తు పద్ధతిని ఉపయోగించి సాధించ గలం. మీరు చేయగలరా ? ఎలా ? ఆలోచించు.
సాధన :
4 నోటు పుస్తకాల వెల = ₹ 80
ఒక నోటు పుస్తకము వెల = 80 ÷ 4 = ₹ 20
7 నోటు పుస్తకముల వెల = ₹ 20 × 7
= ₹ 140
![]()
నీ ప్రగతిని సరిచూసుకో, [పేజి నెం. 14]
→ క్రింద ఇవ్వబడిన పట్టికలో రాశులు అనులోమాను పాతంలో ఉంటే ఖాళీలను పూరించండి :

సాధన :

ఇవి చేయండి కృత్యం [పేజి నెం. 16]
ఒక గడియారంని తీసుకుని నిమిషాల ముల్లు ఏదైనా ఒక సంఖ్య దగ్గర ఉంచండి. (ఇది 12 దగ్గర అయితే సులభం అవుతుంది) అప్పటి నుండి ప్రతి 15 నిమిషాల వ్యవధిలో ఆ ముల్లు చేసిన కోణాన్ని కనుక్కొని, నమోదు చేయండి.
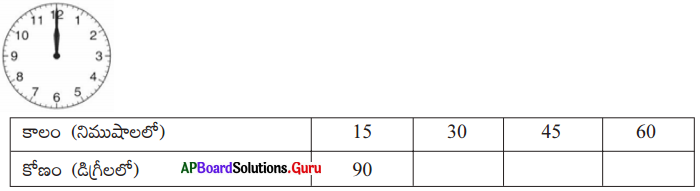
పై రాశులు అనులోమానుపాతంలో ఉన్నాయో, లేదో పరీక్షించండి.
సాధన.

అన్ని సందర్భాలలో x : y సమానంగా కలదు. కావున ఇచ్చిన రాశులు అనులోమానుపాతంలో కలవు.
![]()
ఆలోచించండి [పేజి నెం. 16]
ప్రశ్న 1.
నిమిషాల ముల్లు ఒక నిముషంలో చేయు కోణం ఎంత?
సాధన.
నిమిషాల ముల్లు ఒక నిముషంలో చేయు కోణం:
1 గంటలో నిమిషాల ముల్లు చేయు కోణం = 360°
(1 గంటకు ఒక భ్రమణాన్ని పూర్తి’ చేస్తుంది.)
60 నిమిషాలలో నిమిషాల ముల్లు చేయు కోణం = 360°
నిమిషాల ముల్లు తిరుగు సమయం మరియు అది చేయు కోణము అనులోమానుపాతంలో ఉంటాయి.
నిమిషాల ముల్లు ఒక నిమిషంలో చేయు కోణం = x° అనుకొందాం.
∴ 60 : 360° = 1 : x
అంత్యముల లబ్దం = మధ్యమముల లబ్దం
⇒ 60 = 60 × x = 360 × 1
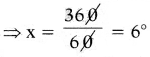
∴ నిమిషాల ముల్లు ఒక నిమిషములో చేయు కోణం = 6°
ప్రశ్న 2.
గంటల ముల్లు ఒక నిముషంలో చేయు కోణం ఎంత?
సాధన.
గంటల ముల్లు ఒక నిమిషంలో చేయు కోణం:
12 గంటలలో గంటల ముల్లు చేయు కోణం = 360°
(గంటల ముల్లు 12 గంటలలో ఒక భ్రమణం పూర్తిచేస్తుంది.)
12 × 60 = 720 నిమిషాలలో గంటల ముల్లు చేయు కోణము = 360°
గంటల ముల్లు తిరుగు సమయం మరియు అది చేయు కోణము అనులోమానుపాతంలో ఉంటాయి.
గంటల ముల్లు ఒక నిమిషములో చేయు కోణం = x° అనుకొందాం.
∴ 720 : 360° = 1 : x°
అంత్యముల లబ్దం = మధ్యమముల లబ్దం
720 × x° = 360 × 1
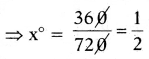
∴ గంటల ముల్లు ఒక నిమిషములో చేయు కోణం = \(\frac{1}{2}^{\circ}\)
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 18]
ప్రశ్న 1.
క్రింద ఇవ్వబడిన రాశులు విలోమానుపాతంలో ఉంటే, ఖాళీలను పూరించండి:

సాధన.

గమనిక: x, y లు విలోమానుపాతంలో ఉంటే
x × y = k కావాలి.
2 × 90 = 180 అలాగే 3 × 60 = 180,
6 × 30 = 180, 5 × 36 = 180,
9 × 20 = 180
లబ్దం 180 అయ్యే విధంగా పట్టికను పూర్తి చేయాలి.
![]()
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 26]
ప్రశ్న 1.
ఈ క్రింద ఇవ్వబడిన పట్టికలో రాశులు ఏ విధమైన సంబంధాన్ని కలిగి ఉన్నాయో విశ్లేషించి ‘x’ విలువను కనుగొనండి.
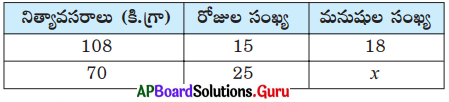
సాధన.
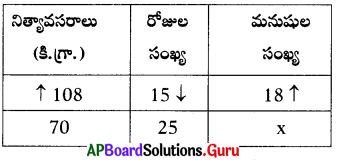
(i) మనుషుల సంఖ్య, రోజుల సంఖ్య విలోమాను పాతంలో ఉంటాయి. (విలోమ నిష్పత్తి తీసుకోవాలి)
(ii) మనుషుల సంఖ్య, నిత్యావసరాల బరువు అనులోమానుపాతంలో ఉంటాయి.
∴ 18 : x = 108 : 70 మరియు 25 : 15 ల బహుళ నిష్పత్తి,
18 : x = 108 × 25 : 70 × 15
మధ్యమముల లబ్దం = అంత్యముల లబ్దం
⇒ x × 108 × 25 = 18 × 70 × 15
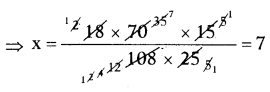
∴ x = 7
ఆలోచించండి [పేజి నెం. 36]
ప్రశ్న 1.
ఒక వ్యక్తి ₹10 కి 10 చాక్లెట్లు కొని, ₹12 కి 10 చాక్లెట్లు అమ్మాడు. అతనికి లాభమా ? నష్టమా ? ఎంత శాతం ?
సాధన.
10 చాక్లెట్లు కొన్నవెల (కొ.వె) = ₹ 10
10 చాక్లెట్లు అమ్మినవెల (అ.వె) = ₹ 12
అ.వె > కొ.వె. కావున లాభం వస్తుంది.
లాభం = S.P – C.P = 12 – 10 = ₹2
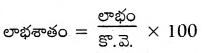
= \(\frac{2}{10}\) × 100 = 20%
(లేదా)
లాభశాతం = x అనుకొనుము.
కొ.వె., లాభం అనులోమానుపాతంలో ఉంటాయి.
10 : 2 = 100 : x
⇒ 10 × x = 2 × 100
⇒ x = \(\frac{2 \times 100}{10}\) = 20%
∴ లాభం = 20%
![]()
ప్రశ్న 2.
ఒక వర్తకుడు తను కొన్న సోఫాలను 50% ధరలను పెంచి, ఆ తర్వాత 50% తక్కువ ధరకు అమ్ముతున్నచో, అది లాభమా ? నష్టమా ?
సాధన.
సోఫా కొన్న వెల = ₹ 100 అనుకొనుము.
![]()
మొత్తం ధర = ₹ 100 + ₹ 50 = ₹ 150
నష్ట శాతం = 50%
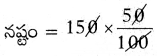
నష్టం = ₹75
అ.వె. = మొత్తం ధర – నష్టం
= 150 – 75 = ₹ 75
కొ.వె. = ₹100; అ.వె. = ₹75
మరియు కొ.వె. > అ.వె.
కనుక, వర్తకుడు 25% నష్టాన్ని పొందాడు.
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 40]
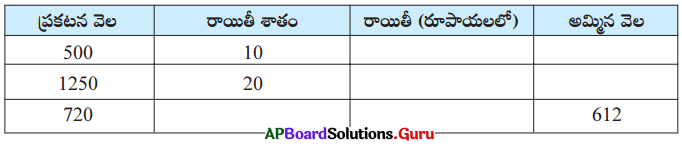
సాధన.
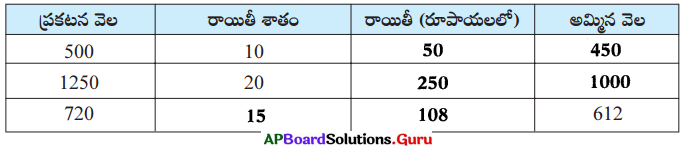
(i) ప్రకటన వెల ₹500, రాయితీ 10%
రాయితీ = ₹500 పై 10%
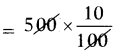
= ₹50
అమ్మిన వెల = ₹500 – ₹50 = ₹450
(ii) ప్రకటన వెల ₹1250, రాయితీ 20%
రాయితీ = ₹1250 పై 20%
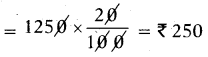
అమ్మిన వెల = ₹1250 – ₹250 = ₹ 1000.
(iii) ప్రకటన వెల ₹720, అమ్మిన వెల = ₹612
రాయితీ = ప్రకటన వెల – అమ్మిన వెల
= ₹720 – ₹612 = ₹ 108
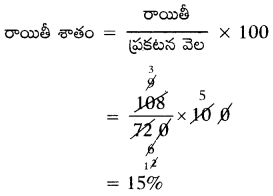
![]()
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 48]

సాధన.
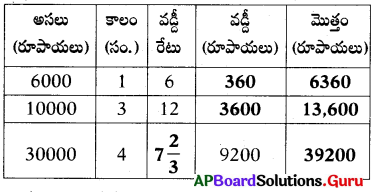
(i). అసలు (P) = 6000; కాలం (T) = 1,
వడ్డీరేటు (R) = 6
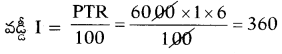
మొత్తం = 6000 + 360 = ₹6360
(ii) అసలు (P) = 10,000, కాలం (T) = 3,
వడ్డీరేటు (R) = 12
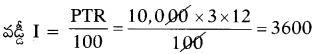
మొత్తం A = P + I
= 10,000 + 3,600 = ₹13,600
(iii) అసలు (P) = 30,000, కాలం ‘ (T) = 4,
వడ్డీరేటు (R) = ?

![]()
ఆలోచించండి [పేజి నెం. 48]
ప్రశ్న 1.
ఎంత వడ్డీ రేటుతో అసలు పది సంవత్సరాలలో రెట్టింపవుతుంది ?
సాధన.
అసలు (P),
కాలం (T) = 10,
వడ్డీరేటు (R) = ?
మొత్తం A = 2P
(అసలు రెట్టింపు కావలెనన్న వడ్డీ అసలుకు సమానం కావాలి. P = I)
∴ I = \(\frac{\text { PTR }}{100}\)
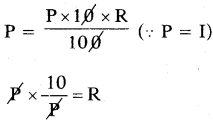
∴ R = 10%
10% వడ్డీరేటుతో అసలు పది సంవత్సరాలలో రెట్టింపు అవుతుంది.
(లేదా)
అసలు (P) = 100 అనుకొనుము.
కాలం (T) = 10 సంవత్సరాలు
వడ్డీరేటు (R) = ?
అసలు P = 100 రెట్టింపు కావలెనంటే
మొత్తం A = 200 కావలెను.
అనగా వడ్డీ I = 100 కావలెను.
I = \(\frac{\text { PTR }}{100}\)
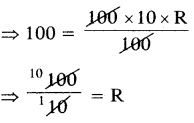
∴ R = 10
10% వడ్డీరేటుతో అసలు పది సంవత్సరాలలో రెట్టింపు అవుతుంది.
![]()
ప్రశ్న 2.
ఎంత వడ్డీ రేటుతో 15 సంవత్సరాలలో అసలు నాలుగు రెట్లు అవుతుంది ?
సాధన.
అసలు (P)
కాలం (T) = 15
వడ్డీరేటు (R) = ?
మొత్తం A = 4P
అసలు నాలుగు రెట్లు కావలెనన్న వడ్డీ అసలుకు 3 రెట్లు కావాలి. అనగా I = 3P కావలెను.
I = \(\frac{\text { PTR }}{100}\)
⇒ 3P = \(\frac{P \times 15 \times R}{100}\)
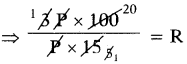
∴ R = 20%
(లేదా)
అసలు (P) = 100 అనుకొనుము.
కాలం (T) = 15 సంవత్సరాలు
వడ్డీరేటు (R) = ?
అసలు నాలుగు రెట్లు కావలెనన్న మొత్తం 400 కావలెను. అనగా వడ్డీ I = 300 కావలెను.
I = \(\frac{\text { PTR }}{100}\)
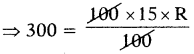
⇒ \(\frac{300}{15}\) = R
∴ R = 20%
∴ 20% వడ్డీ రేటున అసలు 15 సంవత్సరాలలో 4 రెట్లు అవుతుంది.
ఉదాహరణ
ప్రశ్న 1.
8 : 7 మరియు 9 : 13ల బహుళ నిష్పత్తిని కనుగొనుము.
సాధన.
దత్త నిష్పత్తి = 8 : 7 : 9 : 13
(బహుళ నిష్పత్తి = పూర్వ పదాల లబ్ధం : పర పదాల లబ్ధం)
బహుళ నిష్పత్తి = 8 × 9 : 7 × 13 = 72 : 91
![]()
ప్రశ్న 2.
ఇద్దరు స్నేహితులు ప్రభు, సురేష్ ఒక్కొక్కరు ₹1,00,000 తో ఒక వ్యాపారాన్ని ప్రారంభించారు. మూడు నెలల తర్వాత సురేష్ వ్యాపారం నుండి వైదొలిగాడు. సంవత్సరాంతమున వారికి ₹20,000 లాభం వచ్చిన, దానిలో సురేష్ మరియు ప్రభుల లాభాల వాటాలు లెక్కించండి.
సాధన.
ఇక్కడ సురేష్, ప్రభులు ఇద్దరూ ఒక్కొక్కరు
₹1,00,000తో వ్యాపారాన్ని ప్రారంభించారు. ప్రభు సంవత్సరమంతా వ్యాపారంలో కొనసాగాడు.
సురేష్ వ్యాపారంలో మూడు నెలలు మాత్రమే కొనసాగాడు.
వారి యొక్క పెట్టుబడుల నిష్పత్తి
= 1,00,000 : 1,00,000 = 1 : 1
ప్రభు, సురేషన్లు వ్యాపారంలో కొనసాగిన కాలాల నిష్పత్తి
= 12 : 3 = 4 : 1
అందువల్ల, వారి యొక్క లాభాన్ని వారి యొక్క పెట్టుబడులు మరియు కాలాల యొక్క బహుళ నిష్పత్తి ఆధారంగా పంచుకోవాలి.
బహుళ నిష్పత్తి = 1 × 4 : 1 × 1 = 4 : 1
లాభం = ₹20,000
మొత్తం భాగాలు = 4 + 1 = 5
సురేష్ యొక్క లాభం = 20,000 × \(\frac{1}{2}\) = ₹4,000
ప్రభు యొక్క లాభం = 20,000 – 4,000
= ₹ 16,000
ప్రశ్న 3.
రాణి ఒక బ్యూటీపార్లర్ ను ₹ 75,000 పెట్టుబడితో ప్రారంభించింది. నాలుగు నెలల తరువాత వాణి, రాణితో అదే వ్యాపారంలో ₹ 50,000 పెట్టుబడి పెట్టింది. సంవత్సరాంతమున వారిరువురు ₹52,000 లాభాన్ని సంపాదించారు. అయిన రాణి, వాణి లాభాల వాటాలు ఎంతెంత ?
సాధన.
రాణి యొక్క పెట్టుబడి = ₹75,000
రాణి యొక్క వ్యాపార కాలం = 1 సంవత్సరం
= 12 నెలలు
వాణి యొక్క పెట్టుబడి = ₹50,000
వాణి యొక్క వ్యాపార కాలం = 8 నెలలు
రాణి మరియు వాణిల పెట్టుబడుల నిష్పత్తి
= 75,000 : 50,000 = 3 : 2
రాణి మరియు వాణిల వ్యాపార కాలాల నిష్పత్తి
= 12 : 8 = 3 : 2
కావున, వారి యొక్క లాభాన్ని వారి యొక్క పెట్టుబడులు మరియు కాలాల యొక్క బహుళ నిష్పత్తి ఆధారంగా పంచుకోవాలి.
బహుళ నిష్పత్తి = 3 × 3 : 2 × 2 = 9 : 4
లాభం = ₹ 52,000
మొత్తం భాగాలు = 9 + 4 = 13 .
రాణి యొక్క లాభం = 52000 × \(\frac{9}{13}\)
= ₹ 36000
వాణి యొక్క లాభం = 52000 – 36000
= ₹ 16,000
![]()
ప్రశ్న 4.
3 : 4 మరియు 9 : x లు అనులోమానుపాతంలో ఉంటే x విలువ ఎంత?
సాధన.
3 : 4 మరియు 9 : x అనులోమానుపాతంలో ఉంటే వాటి నిష్పత్తి స్థిరము.
∴ \(\frac{3}{4}\) = \(\frac{9}{x}\)
⇒ 3 × x = 4 × 9
⇒ x = \(\frac{4 \times 9}{3}\) = 12
ప్రశ్న 5.
4 నోటు పుస్తకాల వెల ₹80 అయిన 7 నోటు పుస్తకాల వెల ఎంత ?
సాధన.

ఇక్కడ నోటు పుస్తకాల సంఖ్య పెరిగిన, వాటి వెల కూడా పెరుగుతుంది. అదే విధంగా నోటు పుస్తకాల సంఖ్యకు, వాటి వెలకు గల నిష్పత్తి స్థిరము. అనగా ఇక్కడ నోటు పుస్తకాల సంఖ్య, వాటి వెల అనులోమాను పాతంలో ఉన్నాయి.
ఆ ఏడు నోటు పుస్తకాల వెల ‘x’ అనుకున్నచో,
అప్పుడు 4 : 80 = 7 : x
నిష్పత్తులు సమానం అయినప్పుడు,
అంత్యముల లబ్దం = మధ్యమముల లబ్దం –
4 × x = 80 × 7
⇒ x = \(\frac{80 \times 7}{4}\)
= ₹ 140
∴ 7 నోటు పుస్తకాల వెల = ₹ 140
ప్రశ్న 6.
ఒక పటాన్ని 1 : 30000 స్కేలు (పరిమాణం)తో గీయబడింది. పటంలో రెండు పట్టణాల మధ్య దూరం 20 సెం.మీ. అయిన, రెండు పట్టణాల మధ్య వాస్తవ దూరం ఎంత ?
సాధన.
పటంలో ఉన్న దూరానికి, వాస్తవ దూరం అనులోమాను
పాతంలో ఉంటుందని మనం గమనించవచ్చు. రెండు పట్టణాల మధ్య వాస్తవ దూరం ‘X’ అనుకున్నచో,
1 : 30000 = 20 : x
నిష్పత్తులు సమానం కావున, అంత్యముల లబ్దం = మధ్యమముల లబ్దం
∴ 1 × X = 30,000 × 20
⇒ x = 6,00,000 సెం.మీ. = 6 కి. మీ.
[1,00,000 సెం.మీ. = 1000 మీ. = 1 కి.మీ.]
పటంలో 20 సెం.మీ. దూరంలో ఉన్న పట్టణాల మధ్య వాస్తవ దూరం = 6 కి. మీ.
![]()
ప్రశ్న 7.
4, 7 మరియు 2, x లు విలోమానుపాతంలో ఉంటే, x విలువ ఎంత?
సాధన.
4, 7 మరియు 2, x లు విలోమానుపాతంలో ఉన్నాయి.
అందువల్ల, 4 × 7 = 2 × x
⇒ x = \(\frac{4 \times 7}{2}\) = 14
ప్రశ్న 8.
18 మంది పనివాళ్ళు ఒక గోడను 12 రోజులలో కట్టగలరు. అయిన ఎనిమిది మంది పనివాళ్ళు, అలాంటి గోడను ఎన్ని రోజులలో నిర్మించగలరు ?

సాధన.
పనివాళ్ళ సంఖ్య తగ్గుతూ ఉంటే, గోడ కట్టడానికి పట్టే రోజుల సంఖ్య పెరుగుతుంది. కావున, పనివాళ్ళ సంఖ్య మరియు గోడ కట్టడానికి పట్టే రోజుల సంఖ్య విలోమానుపాతంలో ఉంటాయి.
గోడ కట్టడానికి పట్టే రోజుల సంఖ్య ‘X’ అనుకొనుము.
| పనివాళ్ళ సంఖ్య | రోజుల సంఖ్య |
| 18 | 12 |
| 8 | x |
విలోమానుపాతాన్ని తీసుకుంటే,
18 : 8 = x : 12
అప్పుడు, 18 × 12 = 8 × x
= 8 × x = 18 × 12
⇒ x = \(\frac{18 \times 12}{8}\) = 27 రోజులు
∴ కావున, ఎనిమిది మంది పనివాళ్ళు 27 రోజులలో గోడను నిర్మించగలరు.
ఇది పరిశీలించండి:
విలోమానుపాతంలో ఉంటే, లబ్దం ఎల్లప్పుడూ స్థిరం.
18 × 12 = 8 × X
⇒ 8 × x = 18 × 12
⇒ x = \(\frac{18 \times 12}{8}\)
= 27 రోజులు
ప్రశ్న 9.
ఒక పెద్ద నీళ్ళ తొట్టెను నాలుగు పంపులు 1 గం. 30ని. లలో నింపగలవు. అదే తొట్టెను 3 పంపులు ఎంత సమయంలో నింపగలవు?

సాధన.
సమయం ‘X’ అనుకుంటే
1 గం. 30 ని. = 60 + 30 = 90 ని.
పంపుల సంఖ్య తగ్గుతూ ఉంటే, నీళ్ళ తొట్టె నిండడానికి పట్టే సమయం పెరుగుతూ ఉంటుంది.
కనుక పంపుల సంఖ్య, తొట్టె నిండే సమయం విలోమానుపాతంలో ఉండును.
| పైపుల సంఖ్య | నింపడానికి పట్టే కాలం (ని.) |
| 4 | 90 |
| 3 | x |
విలోమానుపాతాన్ని తీసుకుంటే:
4 : 3 = x : 90
అప్పుడు, 4 × 90 = 3 × x
⇒ 3 × x = 4 × 90
⇒ x = \(\frac{4 \times 90}{3}\) = 120 ని.
∴ కావున, మూడు పంపులు కలిపి ఆ నీళ్ళ తొట్టెను 120 ని. లేదా 2 గం.లలో నింపగలవు.
ఇది పరిశీలించండి:
విలోమానుపాతంలో ఉంటే, లబ్దం ఎల్లప్పుడూ స్థిరం.
4 × 90 = 3 × x
⇒ 3 × x = 4 × 90
⇒ x = \(\frac{4 \times 90}{3}\) = 120 ని.
![]()
ప్రశ్న 10.
30 మంది వ్యక్తులు 40 కి.గ్రా. చక్కెరను పది రోజులలో వాడిన, 80 మంది వ్యక్తులు 320 కి.గ్రా.ల చక్కెరను ఎన్ని రోజులలో వినియోగిస్తారు? ఎలా సాధిస్తాం?
సాధన.
ఇక్కడ 3 రాశులు ఉన్నాయి. అవి మనుషుల సంఖ్య, చక్కెర బరువు మరియు రోజుల సంఖ్యలు.
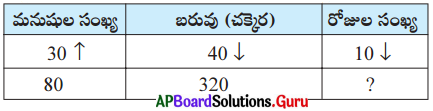
పై పట్టిక నుండి తెలియని రాశిని తెలిసిన రాశులతో వేర్వేరుగా పోల్చగలరు.
→ రోజుల సంఖ్య మరియు వ్యక్తుల సంఖ్య రెండు రాశులు విలోమానుపాతంలో ఉంటాయి. దీనిని ↑ గుర్తుతో సూచించాం.
→ రోజుల సంఖ్య మరియు చక్కెర బరువు రెండు రాశు లు అనులోమానుపాతంలో ఉంటాయి. దీనిని ↓ గుర్తుతో సూచించాం.
ఇక్కడ రోజుల సంఖ్య, వ్యక్తుల సంఖ్య మరియు చక్కెర బరువులు రెండింటిపై ఆధారపడుతుంది. కావున, మనం 80 : 30 మరియు 40 : 320 బహుళ నిష్పత్తులను తీసుకోవాలి.
∴ 10 : x = 80 × 40 : 30 × 320
= 3200 : 9600
నిష్పత్తులు సమానం కావున, అంత్యముల లబ్దం, మధ్యమముల లబ్దానికి సమానం.
10 : x = 3200 : 9600
⇒ 10 × 9600 = x × 3200
⇒ x × 3200 = 10 × 9600
⇒ x = \(\frac{10 \times 9600}{3200}\) = 30
ప్రశ్న 11.
8 మంది రంగులు వేసేవారు 160 మీ. పొడవు గల ఒక గోడకు, 5 రోజులలో రంగులు వేయగలరు. 240మీ. పొడవు గల గోడకు, 10 రోజులలో రంగు వేయుటకు ఎంత మంది పనివాళ్ళు కావలెను ?
సాధన.
ఇక్కడ మూడు రాశులు అనగా రంగులు వేసేవారి సంఖ్య, గోడ పొడవు మరియు రోజుల సంఖ్య గలవు.

రంగులు వేసేవారి సంఖ్య, గోడ పొడవు అనులోమాను పాతంలో ఉంటాయి.
రంగులు వేసేవారి సంఖ్య, రోజుల సంఖ్యకు విలోమాను పాతంలో ఉంటాయి.
రంగులు వేసేవారి సంఖ్య, గోడ పొడవు మరియు రోజుల సంఖ్య రెండింటిపైనా ఆధారపడి ఉండడం వల్ల మనం 160 : 240 మరియు 10 : 5 నిష్పత్తుల బహుళ నిష్పత్తిని తీసుకోవాలి.
∴ 8 : x = 160 × 10 : 240 × 5
నిష్పత్తులు సమానం. కావున, అంత్యముల లబ్దం, మధ్యమముల లబ్దానికి సమానం.
8 : x = 160 × 10 : 240 × 5
⇒ x × 160 × 10 = 8 × 240 × 5
⇒ x = \(\frac{8 \times 240 \times 5}{160 \times 10}\) = 6
రంగులు వేయుటకు కావల్సినవారి సంఖ్య = 6
![]()
ప్రశ్న 12.
195 మంది పురుషులు రోజుకి పది గంటలు చొప్పున పనిచేసిన, 20 రోజులలో ఒక పనిని పూర్తి చేయగలరు. అదే పనిని రోజుకి 13 గంటల చొప్పున పనిచేస్తూ, 15 రోజులలో పూర్తి చేయుటకు ఎంత మంది పురుషులు అవసరమవుతారు ?
సాధన.
ఇక్కడ 3 రాశులు అనగా పురుషుల సంఖ్య, రోజుల సంఖ్య మరియు రోజుకి పనిచేసిన గంటలు కలవు.

ఇక్కడ పురుషుల సంఖ్య, రోజుకి పనిచేసిన గంటల సంఖ్య విలోమానుపాతంలో ఉంటాయి.
పురుషుల సంఖ్య, రోజుకి పని చేసిన గంటలు మరియు రోజుల సంఖ్య రెండింటిపై ఆధారపడి ఉండడం వల్ల మనం 13 : 10 మరియు 15: 20 నిష్పత్తుల బహుళ నిష్పత్తిని తీసుకోవాలి.
కావున 195 : x = 13 × 15 : 20 × 10
నిష్పత్తులు సమానం. కావున, అంత్యముల లబ్దం, మధ్యమముల లబ్దానికి సమానం.
⇒ x × 13 × 15 = 195 × 20 × 10
⇒ x = \(\frac{195 \times 20 \times 10}{13 \times 15}\) = 200
కావున, అవసరమైన పురుషుల సంఖ్య = 200
ప్రశ్న 13.
క్రింది శాతాలను భిన్నాలుగా, దశాంశాలుగా మరియు నిష్పత్తులుగా రాయండి.
(i) 45%
సాధన.
45% = \(\frac{45}{100}\) = \(\frac{9}{20}\) (భిన్నం)
= 0.45 (దశాంశం)
= 9:20 (నిష్పత్తి)
(ii) 62%
సాధన.
62% = \(\frac{62}{100}\) = \(\frac{31}{50}\) (భిన్నం)
= 0.62 (దశాంశం)
= 31:50 (నిష్ప త్తి)
ప్రశ్న 14.
150 లో 24% కనుక్కోండి మరియు ఆ సంఖ్యలో మిగిలిన సంఖ్యను కనుక్కోండి.
సాధన.
150 లో 24% = \(\frac{24}{100}\) × 150 = 36
ఆ సంఖ్యలో మిగిలిన సంఖ్య
= 150 – 36 = 114
![]()
ప్రశ్న 15.
రఘు పెన్నులను ₹ 400 కొని, ₹ 480 కి అమ్మిన, అతని లాభం లేదా నష్టశాతాన్ని కనుగొనండి.
సాధన.
తరగతిలోని జ్యోతి అనే విద్యార్థి ఈ విధంగా సాధించింది:
రఘు పెన్ను కొన్నవెల = ₹ 400,
అమ్మినవెల = ₹480
అమ్మినవెల > కొన్నవెల కావున రఘుకి లాభం వస్తుంది.
లాభం = 480 – 400 = ₹80
లాభ శాతం = \(\frac{80}{400}\) × 100 = 20%
విద్యార్థి అన్వర్ ఈ క్రింది విధంగా సాధించాడు:
రఘు పెన్ను కొన్నవెల = ₹ 400,
అమ్మినవెల = ₹480
లాభం = అమ్మినవెల – కొన్నవెల
= 480 – 400 = ₹80
లాభానికి, కొన్నవెలకి గల నిష్పత్తి లేదా భిన్నం \(\frac{80}{400}\).
∴ లాభ శాతం = \(\frac{80}{400}\) × 100 = 20%
విద్యార్ధి సురేష్ అనుపాతాన్ని ఉపయోగించి ఇలా చేశాడు:
రఘు కొన్నవెల ₹400 అయితే లాభం ₹80, కొన్నవెల ₹100 అయితే లాభం ‘X’ అనుకొనుము. ఇక్కడ కొన్నవెల మరియు లాభం అనులోమాను పాతంలో ఉన్నాయి.
x : 80 = 100 : 400
⇒ \(\frac{x}{80}\) = \(\frac{100}{400}\)
⇒ x × 400 = 100 × 80
⇒ x = \(\frac{100 \times 80}{400}\) = 20%
లాభం = 100 కి 20
లాభ శాతం = 20%
ప్రశ్న 16.
రమణ ఒక సైకిలును ₹1200 కి కొని, తన స్నేహితుడు రెహమానకు ₹900 కి అమ్మాడు. అయితే రమణ యొక్క లాభం లేదా నష్టశాతాన్ని కనుక్కోండి.
సాధన.
రమణ యొక్క కొన్న వెల = ₹1200
అమ్మిన వెల = ₹ 900
ఇక్కడ అ.వె. < కొ.వె. కావున రమణకి నష్టం వస్తుంది.
నష్టం = కొ.వె. – అ.వె. ఆ
= 1200 – 900 = ₹ 300
నష్టశాతం = \(\frac{300}{1200}\) × 100 = 25%
![]()
ప్రశ్న 17.
జాన్ ఒక కారును ₹ 1,50,000 కొన్నాడు. 10% లాభానికి అతను కారును అమ్మిన వెల కనుక్కోండి.

సాధన.
కొన్న వెల = ₹1,50,000
లాభం % = 10%
అనగా లాభం = ₹1,50,000 లో 10%
= \(\frac{10}{100}\) × 150000
= ₹ 15000
అ.వె. = కొ.వె. + లాభం
= ₹1,50,000 + ₹ 15000
= ₹1,65,000
ఈ సమస్యను అనుపాతాన్ని ఉపయోగించి సాధించవచ్చు:
లాభం 10% అనగా,
కొ.వె. ₹ 100 అయితే లాభం ₹ 10
అప్పుడు అ.వె. = ₹100 + ₹ 10
= ₹110
ప్రస్తుత సమస్యలో కొ.వె. = ₹ 1,50,000
అ.వె. = x అనుకుంటే
కొ.వె. మరియు అ.వె. అనులోమానుపాతంలో ఉంటాయి.

![]()
ప్రశ్న 18.
కిరణ్ ఒక రిఫ్రిజిరేటర్ను ₹16800కి అమ్మితే అతనికి లాభం వచ్చిన, ఆ రిఫ్రిజిరేటర్ కొన్నవెల ఎంత ?

సాధన.
రూప ఈ సమస్యను ఏకవస్తు పద్ధతిని ఉపయోగించి చేసింది.
అ.వె. = 16,800
లాభం % = 12%
కొ.వె ₹ 100 అయితే, లాభం ₹12
కావున అ.వె = ₹ 112
అనగా కొ.వె ₹ 100 అయితే అ.వె ₹ 112
అ.వె కనుక ₹ 1 అయితే, కొ.వి = \(\frac{100}{112}\)
ఇక్కడ అ.వె ₹ 16,800
కనుక, \(\frac{100}{112}\) × 16,800
కొ.వె = ₹ 15,000
స్నేహ ఈ సమస్యను అనుపాతాన్ని ఉపయోగించి క్రింది విధంగా సాధించింది:
లాభం % = 12%, అ.వె. = ₹ 16800
కొ.వె ₹100 అయితే, లాభం ₹12.
అప్పుడు ఆ.వె. = ₹112
ఇక్కడ అ.వె₹ 16,800
కొ.వె = ‘x’ అనుకుంటే
కొ.వె మరియు అ.వే లు అనులోమానుపాతంలో ఉంటాయి.
∴ \(\frac{x}{16800}\) = \(\frac{100}{112}\)
⇒ x = \(\frac{100 \times 16800}{112}\) = ₹15000
ప్రశ్న 19.
ఒక వస్తువు యొక్క ధర ప్రతి సంవత్సరం, దాని ముందు సంవత్సరం కంటే 10% తగ్గుతూ ఉంటుంది. 2 సంవత్సరాల తర్వాత ఆ వస్తువు వెల ₹ 32,400 అయిన, దాని అసలు వెల ఎంత ?
సాధన.
ఒక వస్తువు వెల మొదటి సంవత్సరం ప్రారంభమున ₹ 100 అయితే, రెండవ సంవత్సరం ప్రారంభానికి అనగా మొదటి సంవత్సరం పూర్తయ్యేసరికి 10% తగ్గుతుంది. అనగా దాని వెల ₹ 90 అవుతుంది. రెండవ సంవత్సరం పూర్తయ్యేసరికి అనగా 3వ సంవత్సరం ప్రారంభానికి దాని వెల 10% తగ్గుతుంది. అనగా 90 లో 10% తగ్గుతుంది.
90 – 9 = ₹ 81
₹ 100 వెల కలిగిన ఒక వస్తువు, 2 సంవత్సరాల తర్వాత దాని వెల ₹81 అవుతుంది.
వస్తువు వెల ప్రారంభంలో ₹ ‘x’ అనుకుంటే
2 సంవత్సరాల తర్వాత దాని వెల ₹ 32,400
కావున, ప్రారంభపు వెలల నిష్పత్తి = 2 సంవత్సరాల తర్వాత వెలల నిష్పత్తి అవుతుంది.
⇒ x : 100 = 32400 : 81
⇒ \(\frac{x}{100}\) = \(\frac{32400}{81}\)
⇒ x = \(\frac{32400 \times 100}{81}\) = ₹ 40000
![]()
ప్రశ్న 20.
రాయితీలను కనుక్కోండి.
(i) ప్రకటన వెల ₹450, అమ్మిన వెల = ₹415
(ii) ప్రకటన వెల ₹810, అమ్మిన వెల = ₹ 765
సాధన.
(i) రాయితీ = ప్రకటన వెల – అమ్మిన వెల
= 450 – 415 = ₹35.
(ii) రాయితీ = ప్రకటన వెల 7 అమ్మిన వేల
= 810 – 765 = ₹45.
ప్రశ్న 21.
ఒక వస్తువు యొక్క ప్రకటన వెల ₹ 400, రాయితీ ₹40 అయిన రాయితీ శాతాన్ని కనుక్కోండి.
సాధన.
రాయితీ = ₹40; ప్రకటన వెల = ₹400
రాయితీ శాతం = \(\frac{40}{400}\) × 100 = 10
ప్రశ్న 22.
ఒక వర్తకుడు వస్తువులను, తను కొన్న వెల కంటే 20% అదనంగా పెంచి, తర్వాత 10% రాయితీపై వస్తువులను అమ్ముతున్నాడు. అతని యొక్క లాభశాతం ఎంత ?
సాధన.
కొన్నవెల వంద రూపాయలు అనుకుంటే
ప్రకటన వెల = 100 + 20 = ₹ 120
రాయితీ = 10%
రాయితీ = \(\frac{10}{100}\) × 120 = 12%
అమ్మిన వెల = ప్రకటన వెల – రాయితీ
= ₹120 – ₹ 12 = ₹108
లాభం = 108 – 100 = ₹8
లాభ శాతం = \(\frac{8}{100}\) × 100 = 8%
రాయితీ తర్వాత వర్తకుడు 8% లాభాన్ని పొందుతాడు.
ప్రశ్న 23.
సాధారణ వడ్డీ మరియు మొత్తాలను లెక్కించండి. –
(i) అసలు ₹5000, కాలం 2 సంవత్సరాలు, వడ్డీ 10%
(ii) అసలు ₹25000, కాలం 3 సంవత్సరాలు, వడ్డీ 12%
సాధన.
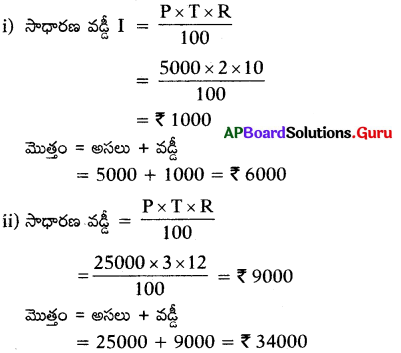
![]()
ప్రశ్న 24.
రహీం ₹25000 ను, సంవత్సరానికి 10% వడ్డీతో అప్పు తీసుకున్నాడు. అయితే మూడు సంవత్సరాలకి అయ్యే సాధారణ వడ్డీ ఎంత ?
సాధన.
పై సమస్యను రాజేష్ క్రింది విధంగా చేశాడు :
అసలు = ₹25000; కాలం = 3 సంవత్సరాలు
వడ్డీ రేటు = 10%
సాధారణ వడీ I = \(\frac{\mathrm{P} \times \mathrm{T} \times \mathrm{R}}{100}\)
= \(\frac{25000 \times 3 \times 10}{100}\) = ₹ 7500
మొత్తం = అసలు + వడ్డీ
= ₹ 25000 + ₹ 7500 = ₹ 32500
సంగీత ఈ క్రింది విధంగా చేసింది:
ఒక సంవత్సరానికి మనం చెల్లించవలసింది 10% మూడు సంవత్సరాలకి వడ్డీ = 3 × 10 = 30%
సాధారణ వడ్డీ = \(\frac{30}{100}\) × 25000 = ₹ 7500
మొత్తం = ₹ 25000 + ₹ 7500 = ₹ 32500
ప్రశ్న 25.
ఎంత సొమ్ముపై సంవత్సరానికి 9% వడ్డీతో, 3 సంవత్సరాల 4 నెలల కాలానికి, సాధారణ వడ్డీ ₹6000 అవుతుంది ?
సాధన.
సాధారణ వడ్డీ = ₹6000

![]()
ప్రశ్న 26.
ఎంత శాతం వడ్డీ రేటుతో, అసలు ₹70000కి \(2^{1 / 2}\) సంవత్సరాలలో సాధారణ వడ్డీ₹14000 అవుతుంది?
సాధన.
అసలు = ₹ 70000
కాలం = \(2^{1 / 2}\) సంవత్సరాలు = \(\frac{5}{2}\) సంవత్సరాలు
సాధారణ వడ్డీ = ₹ 14000
