AP State Syllabus AP Board 7th Class Maths Solutions Chapter 6 Ratio – Applications Ex 5 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 6th Lesson Ratio – Applications Exercise 5
![]()
Question 1.
A shopkeeper bought a suit case for ₹ 480 and sold it for ₹ 540. Find his gain percent?
Solution:
C.P of the suitcase = ₹ 480
SP of the suitcase = ₹ 540
∴ gain=S,P-C.P = 540 – 480 = ₹ 60
∴ gain percent = \(\frac { 60 }{ 450 }\) × 100% = 12.5%
Question 2.
Ajay bought a TV for ₹ 15000 and sold it for ₹141 00. Find the loss percent?
Solution:
C.P of the TV = ₹ 15,000
S.P of the TV = ₹ 14100
As S.P < C.P
Loss = C.P – S.P= 15,000 – 14,100 = ₹ 900
∴ Loss percent = \(\frac { 900 }{ 15000 }\) × 100 = 6%
![]()
Question 3.
Ramu sold a plot of land for ₹ 2,40,000 gaining 20%. For how much did he purchase the plot?
Solution:
Let the cost price of the land = ₹ x
gain percent = 20% of the C.P
∴ S.P of the land = 120% of C.P
By problem, 120% of x = 2,40,000
\(\frac { 120. x }{ 100 }\) = 2,40,000
x = 2.40000 × \(\frac {100 }{ 120 }\)
= ₹ 2,00,000
(OR)
Let the C.P of the land = ₹ x
gain percent = 20% of C.P = 20% of x = \(\frac{20 \mathrm{x}}{100}\)
∴ S.P of the land = C.P + gain
= x + \(\frac{20 \mathrm{x}}{100}\)
= \(\frac{100 x+20 x}{100}=\frac{120 x}{100}\)
By problem, \(\frac{20 \mathrm{x}}{100}\) = 2,40.000
∴ x = 24000 x \(\frac { 100 }{ 120 }\)
= ₹ 2,00,000
![]()
Question 4.
On selling a mobile for ₹ 750, a shop keeper looses 10%. For what amount should he sell it to gain 5%?
Solution:
Let the C.P of the mobile be x
Losspercent = 10% of C.P = 10% of x = \(\frac{10 \mathrm{x}}{100}\)
∴ Loss = \(\frac{10 x}{100}\)
∴ S.P = C.P – Loss
= \(x – \frac{10 x}{100}=\frac{100 x-10 x}{100}=\frac{90 x}{100}\)
By problem, \(\frac{90 \mathrm{x}}{100}\) = 750
x = 750 × \(\frac { 100 }{ 90 }\) = ₹ \(\frac { 2500 }{ 3 }\)
Now to gain by 5% the S.P = C.P + 5% of C.P
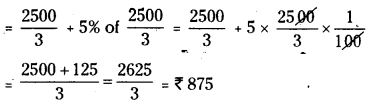
Question 5.
A farmer sold 2 bullocks for ₹ 24000 each. On one bullock he gained 25% and on the other he lost 20%. Find his total profit or loss percent?
Solution:
Let the C.P of first bullock be x
gain = 25% of x = 25 × \(\frac{x}{100}=\frac{25 x}{100}\)
S.P = C.P + gain = x + \(\frac{25 x}{100}=\frac{100 x+25 x}{100}=\frac{125 x}{100}\)
Selling price of first bullock 24,000 (given)
\(\frac{125 x}{100}\) = 24000
x = \(\frac{24000}{125}\) × 100
∴ C.P of first bullock = ₹ 19.200
Let the C.P of second bullock be y
Loss percent = 20%
∴Loss = \(\frac{20 \times \mathrm{y}}{100}=\frac{20 \mathrm{y}}{100}\)
S.P = C.P – loss
= \(y-\frac{20 y}{100}=\frac{100 y-20 y}{100}=\frac{80 y}{100}\)
But S.P = ₹ 24,000 (given)
\(\frac{80 \mathrm{y}}{100}\) = 24,000
∴ y = 24000 x \(\frac{100}{80}\) = 30,000
∴ C.P of second bullock = ₹ 30,000
C.P of 2 bullocks = ₹19,200 + ₹30,000
= ₹ 49,200
S.P of 2 bullocks ₹24,000 × 2 = ₹48,000
Loss = C.P – S.P = 49,200 – 48,000 = ₹1200
Loss % = \(\frac{\text { loss }}{\text { CP }}\) × 100
= \(\frac{1200}{49200}\) × 100 = 2.4
∴ Loss% = 2.4%
![]()
Question 6.
Sravya bought a watch for ₹480. She sold it to Ridhi at a gain of 6\(\frac { 1 }{ 4 }\) %. Ridhi sold it to Divya at a gain of 10%. How much did Divya pay for it?
Solution:
CF of the watch = ₹ 480
Gain% = \(6 \frac{1}{4} \%=\frac{25}{4} \%\)
Gain = 480 × \(\frac{25}{4}\) x \(\frac{1}{100}\) = 30
C.P of the watch for Ridhi = 480 + 30 = ₹ 510
Gain% = 10%
∴ Gain= 51% × \(\frac{10}{100}\) = 51
S.P of the watch for Ridhi = 510 + 51 = ₹561
∴ Amount paid for Divya for the watch = ₹561
Question 7.
The marked price of a book is ₹225.Thc publisher allows a discount of ₹10% on it. Find the selling price of it?
Solution:
The marked price of the book = ₹ 225
Discount 10%
∴ Discount = 225 × \(\frac{10}{100}\)= ₹ 22.5
S.P = M.P – discount
= 225 – 22.5 = ₹202.5
∴ Selling price of the book = ₹ 202.5
![]()
Question 8.
A carpenter allows 15% discount on his goods. Find the marked price of a chair which is sold by him for ₹680?
Solution:
Let the marked price of chair be ₹x
Discount = 15% = x × \(\frac{15}{100}=\frac{15 x}{100}\)
S.P = M.P – discount
\(x-\frac{15 x}{100}=\frac{100 x-15 x}{100}=\frac{85 x}{100}\)
S.P = ₹ 680 (given)
∴ \(\frac{85 \mathrm{x}}{100}\) = 680
x = \(\frac{680 \times 100}{85}\) = 800
Marked price of the chair = ₹ 800
![]()
Question 9.
A dealer allows a discount of ₹ 10% and still gains by 10%. What should be the marked price if the cost price is ₹900?
Solution:
Given that C.P = 900
There is a gain of 10% on C.P
∴ Gain = 10% of ₹ 900
= \(\frac{10 \times 900}{100}\) = ₹ 90
∴ S.P = C.P . gain
= 900 + 90
S.P = ₹990 …………….. (1)
Let the marked price = ₹ x
Discount on it = 10% on M.P = \(\frac{10 \mathrm{x}}{100}\)
∴ Selling Price = MP – Discount
= x – \(\frac{10 \mathrm{x}}{100}\)
= \(\frac{100 x-10 x}{100}\)
∴ S.P = \(\frac{90 \mathrm{x}}{100}\) …………….(2)
From (1) & (2) \(\frac{90 \mathrm{x}}{100}\) = 990
∴ x = 990 x \(\frac{100}{90}\)
∴ M.P = x = ₹1100