AP State Syllabus AP Board 7th Class Maths Solutions Chapter 6 Ratio – Applications Ex 2 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 6th Lesson Ratio – Applications Exercise 2
![]()
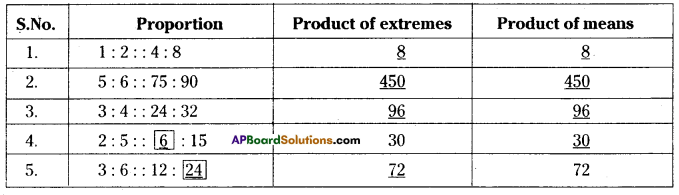
Question 1.
Find the missing in the following proportion in the table given below.
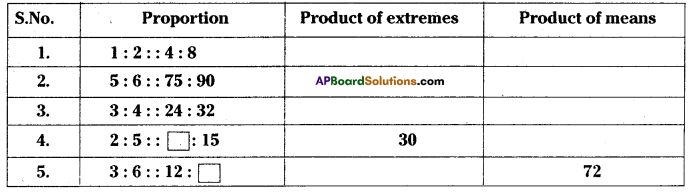
Solution:
Question 2.
Write true or false.
(i) 15 : 30 : : 30 : 40
(ii) 22 : 11 : : 12 : 6
(iii) 90 : 30 : : 36 : 12
(iv) 32 : 64 : : 6 : 12
(v) 25 : 1 : : 40 : 160
Solution:
i) Product of extremes = 15 x 40 600
Prod uct of means 30 x 30 = 900
600 ≠ 900
ii) 22 11:; 12:6 -True
Product oi extremes 22 x 6 = 132
Product of means = 11 x 12 = 132
iii) 90 : 30 :: 36 : 12 -True
Product oi extremes = 90 x 12 = 1080
(5 x 2 = 10 M)
Product of means = 30 x 36 = 1080
1080 = 1080
iv) 32 : 64 :: 6 : 12 -True
Product of extremes = 32 x 12 = 384
Product of means = 64 x 6 = 384
v) 25 : 1 :: 40 : 1.60 – True
Product of extremes = 25 x 1.60 = 40.00
Product of means = 1 x 40 = 40
![]()
Question 3.
Madhu buys 5 kg of potatoes at the market. If the cost of 2 kg is ₹ 36, how much will Madhu pay?
Solution:
Cost of 2 kg potatoes = ₹.36
∴ Cost of 1 kg potatoes = \(\frac{36}{2}\) = ₹.18
Cost of 5kg potatoes @ ₹.18 = 5 × ₹.18 = ₹.90
∴ Madhu pays ₹.90
(OR)
Let Madhu pays ₹.x
2 : 36 :: 5 : x
x = \(\frac{36 \times 5}{2}\) = ₹ 90
Question 4.
Physics tells us that weights of an object on the moon is proportional to its weight on Earth.
Suppose a 90 kg man weighs 15 kg on the moon what will a 60 kg woman weigh on the moon?
Solution:
Man’s weight on earth = 90 kg
Man’s weight on moon = 15 kg
Woman’s weight on earth = 60 kg
Let the womans weight on moon = x kg
then 90 : 15 :: 60 : x
Product of means Product of extremes
90x = 15 × 60
x = \(\frac{15 \times 60}{90}\) = 10
∴ Womans weight on the moon = 10 kg
![]()
Question 5.
A disaster relief team consists of engineers and doctors in the ratio of 2 : 5.
(i) If there are 18 engineers, find the number of doc tors.
(ii) If there are 65 doctors, find the number of engineers.
Solution:
i) Ratio of engineers and doctors= 2 : 5
The number of engineers = 18
Let the number of doctors = x
Now 2 : 5 :: 18 : x .
By the rule of proportion
2x = 5 × 18
= \(\frac{5 \times 18}{2}\) = 45
∴ The number of doctors 45
ii) Numbers of doctors = 65
Let the number of engineers = x
then 2 : 5 :: x : 65
By the rule of proportion
5x = 2 × 65
x = \(\frac{2 \times 65}{2}\) = 26
∴ The number of engineers = 26
![]()
Question 6.
The ratio of two angles is 3: 1. Find the
(i) larger angle if the smaller is 180°
(ii) smaller angle if the larger is 63°.
Solution:
i) Given that the ratio of angles = 3 : 1
Smaller angle is given as = 180°
Let the larger angle be x°
then 3: 1 :: x : 180
∴ By rule of proportion
1 . x = 180° × 3
x = 540°
∴ The required larger angle = 540°
ii) The larger angle is given as = 63°
Let the smaller angle be y°
then 3 : 1 :: 63°: y
∴ By rule of proportion
3 × y = 63 × 1
y = \(\frac{63}{3}\) = 21°
∴ The required smaller angle = 21°