SCERT AP 7th Class Maths Solutions Pdf Chapter 5 Triangles Unit Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 5th Lesson Triangles Unit Exercise
Question 1.
How many right angles exist in a triangle?
Answer:
Only one right angle can exist in a triangle.
Question 2.
Which is the longest side in ∆XYZ having right angle at ‘Z’?
Answer:
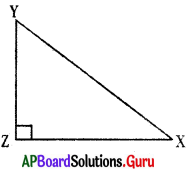
In ∆XYZ, z = 90°
In triangle, the side opposite to the largest angle is longest side. .
So, XY is the longest side in ∆XYZ.
![]()
Question 3.
Is the sum of any two angles of a tri-angle always greater than the third angle? Give examples to justify your answer.
Answer:
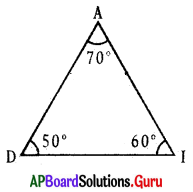
In ∆ADI, ∠A = 70°, ∠D = 50°, ∠I = 60°
∠A + ∠D = 70° + 50° =120° > 60° ∴ ∠A + ∠D > ∠I.
∠D + ∠I = 50° + 60° = 110° > 70° ∴ ∠D + ∠I > ∠A.
∠A + ∠I = 70° + 60° = 130° > 50° ∴ ∠A + ∠I > ∠D.
Yes, sum of any two angles of a triangle always greater than the third angle.
Question 4.
Choose any three measures from the following to make three different triangular wooden frames.
11 m, 9 m, 3 m, 7 m and 5 m.
Answer:
We know that in a triangle sum of any two sides is greater than the third side.
(i) 3m, 7m, 5m
(ii) 3m, 9m, 11m
(iii) 3m, 7m, 9m
Question 5.
Write any two possible measurements to be suitable for the following triangles.
(i) Right angled triangle.
Answer:
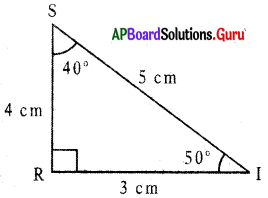
In ∆SRI,
∠S = 40°, ∠R = 90°, ∠I = 50°
SR = 4 cm, RI = 3 cm and SI = 5 cm
(ii) Obtuse angled triangle.
Answer:
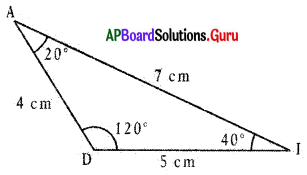
In ∆MDI, .
∠A = 200, ∠D = 1200, ∠I = 40°
AD = 4 cm, DI = 5 cm and AI = 7cm
(iii) Acute angled triangle.
Answer:
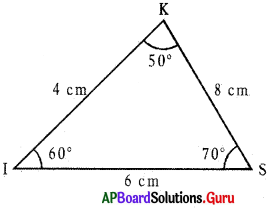
In ∆KIS,
∠K = 50°, ∠I – 60°, ∠S = 70°
KI = 4 cm, IS = 6 cm, KS = 8 cm
![]()
Question 6.
Find the value of ‘x’ and ‘y’ in the adjacent figure.
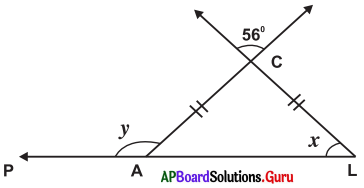
Answer:
In ∆ACL, AC = CL
So, ∆ACL is an isosceles triangle.
In isosceles triangle, the angles which are opposite to equal sides are also equal.
So, ∠A = ∠L = x°
∠C = 56° (Vertically opposite angle)
In ∆ACL,
we know ∠A + ∠C + ∠L = 180°
⇒ x + 56° + x = 180°
⇒ 2x + 56° – 56° = 180° – 56°
⇒ 2x =124°
⇒ \(\frac{2 x}{2}=\frac{124^{\circ}}{2}\)
∴ x = 62°
Exterior angle at A = ∠C + ∠L
⇒ y = 56 + 62
⇒ y = 118°
Question 7.
In ∆ABC, ∠A is four times to ∠B and ∠C is five times to ∠B. Find the three angles.
Answer:
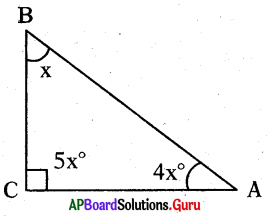
In ∆ABC, let ∠B = x°
then ∠A 4 times of ∠B = 4x°
∠C = 5 times of ∠B = 5x°
In ∆ABC, we know
∠A + ∠B + ∠C = 180°
⇒ 4x + x + 5x = 180°
⇒ 10x = 180°
x = 18°
∠B = 18°,
∠A = 4x° = 4 × 18° = 72°,
∠C = 5x° = 5 × 18° = 90°
∴ Three angles are 18°, 72° and 90°.
![]()
Question 8.
Ladder was faced to a wall, One end of the ladder was making 70° with the floor. Find the angle of the other end of the ladder with the wall.
Answer:
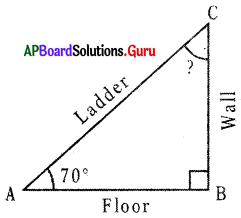
Let A be the one end of the ladder.
C is other end of the ladder.
B is the foot of the wall.
So, ∆ABC is formed.
In ∆ABC, ∠A = 70°, ∠B = 90°
We know, in ∆ABC,
∠A + ∠B + ∠C = 180° ‘
70° + 90° + ∠C = 180°
160° + ∠C = 180°
160° + ∠C – 160° = 180° – 160°
∠C = 20°
So, angle of the other end of the ladder is 20°.
Question 9.
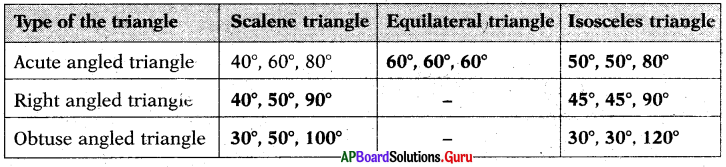
Write the possible measurements of angles in the following table. One example is given for you.
Answer: