SCERT AP 7th Class Maths Solutions Pdf Chapter 4 Lines and Angles Unit Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 4th Lesson Lines and Angles Unit Exercise
Question 1.
Find the complementary, supplementary and conjugate angle of 36°.
Answer:
Complementary angle of 36° is 90° – 36° – 54°
Supplementary angle of 36° is 180° – 36° = 144°
Conjugate angle of 36° is 360° – 36° = 324°
Question 2.
Observe the figure and write any 4 pairs of adjacent angles.
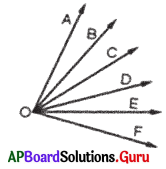
Answer:
Adjacent angle of ∠AOB is ∠BOC.
Adjacent angle of ∠BOC is ∠COD.
Adjacent angle of ∠COD is ∠DOE.
Adjacent angle of ∠DOE is ∠EOF.
Question 3.
In the given figure the lines l and m intersect at O. Find x.
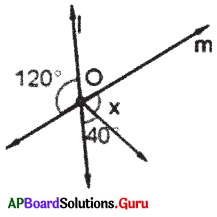
Answer:
Given l and m intersecting at O.
x° + 40° = 120° (vertically opposite angles)
x + 40° – 40°= 120° – 40°
∴ x = 80°
![]()
Question 4.
In the given figure \(\overline{\mathbf{A E}}\) is a straight line. If the ratio of angles ∠1, ∠2, ∠3, ∠4 in the given figure is 1:2 :3 : 4, then find the angles.
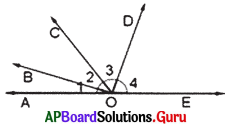
Answer:
Given \(\overline{\mathbf{A E}}\) is a straight line.
Ratio of angles ∠1, ∠2, ∠3, ∠4 is 1 : 2 : 3 : 4 that is 1x: 2x: 3x: 4x
The sum of the angles at a point on the same side of the line is 180°
∠1 + ∠2 + ∠3 + ∠4 = 180°
⇒ 1x + 2x + 3x + 4x = 180°
⇒ 10x = 180
⇒ \(\frac{10 x}{10}=\frac{180}{10}\)
∴ x = 18°
2x = 2 × 18° = 36°
3x = 3 × 18° = 54°
4x = 4 × 18° = 72°
Therefore the angles are 18°, 36°, 54°, 72°.
Question 5.
Write any two examples for linear pair of angles in your surroundings.
Answer:
Electric pole, Tree/Pen stand, etc.
Question 6.
Mani said, “Two obtuse angles can form a pair of conjugate angles.” Do you agree? Justify your answer.
Answer:
Obtuse angle is always less than 180°. Sum of two obtuse angles is less than 360°.
So, I do not agree, that two obtuse angles cannot form a pair of conjugate angles.
Question 7.
Draw a pair of adjacent angles which are not supplementary to each other.
Answer:
(i)
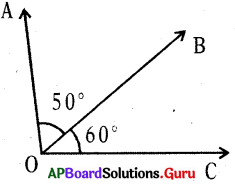
∠AOB and ∠BOC are adjacent angles.
∠AOB + ∠BOC = 50° + 60°
= 110° ≠ 180°
∠AOB and ∠BOC are not supplementary.
(ii)
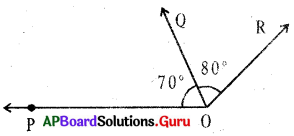
∠POQ and ∠QOR are adjacent angles.
∠POQ + ∠QOR = 70° + 80°
= 150° ≠ 180°
∠POQ and ∠QOR are not supplementary.
Question 8.
In the figure, if l ∥ m, t is a transversal. Find ∠1 and ∠2.
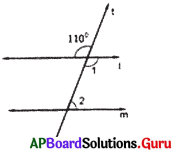
Answer:
Given l ∥ m and t is a transversal.
∠1 = 110° (vertically opposite angles)
∠1 + ∠2 = 180° (co-interior angles are supplementary)
110° + ∠2 = 180°
110° + ∠2 – 110° = 180° – 110°
∠2 – 70°
∠1 = 110° and ∠2 = 70°
![]()
Question 9.
A line p intersects two lines l and m at two distinct points. Observe the figure and fill in the blanks :
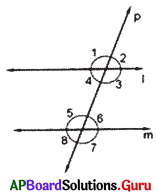
(i) The line ‘p’ is known as ________, ________
(ii) ∠1 and ∠5 is a pair of ________ angles.
(iii) ∠4 and ∠6 is a pair of ________ angles.
(iv) ∠3 and ∠6 is a pair of ________ angles.
Answer:
(i) transversal line,
(ii) corresponding
(iii) alternate interior
(iv) co-interior
Question 10.
In the given figure \(\overrightarrow{\mathbf{C F}} \| \overrightarrow{\mathbf{B D}}, \overrightarrow{\mathbf{B E}}\) is transversal. ∠CAE = 135°, then find ∠ABD
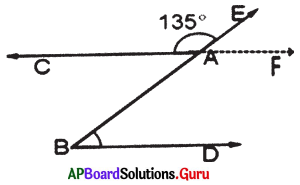
Answer:
Given \(\overrightarrow{\mathrm{CF}} \| \overrightarrow{\mathrm{BD}}\) and \(\overrightarrow{\mathrm{BE}}\) is transversal, ∠CAE — 135°
∠BAF = ∠CAE = 135° (vertically opposite angles)
∴ ∠BAF = 135°
∠BAF + ∠ABD = 180° (co-interior angles are supplementary)
135° + ∠ABD = 180°
135° + ∠ABD – 135° =180°- 135°
∴ ∠ABD = 45°