SCERT AP 7th Class Maths Solutions Pdf Chapter 4 రేఖలు మరియు కోణాలు InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 4th Lesson రేఖలు మరియు కోణాలు InText Questions
నీ ప్రగతిని సరిచూసుకో [పజి నెం. 132]
ప్రశ్న 1.
ఇచ్చిన కోణాలకు పూరక కోణాలను కనుగొనండి.
(i) 27°
సాధన.
27°లకు పూరక కోణం = 90 – 27 = 63°
(ii) 43°
సాధన.
43°లకు పూరక కోణం = 90 – 43 = 47°
![]()
(iii) k°
సాధన.
k°లకు పూరక కోణం = (90 – k)°
(iv) 2°
సాధన.
2° లకు పూరక కోణం = 90 – 2 = 88°
ప్రశ్న 2.
ఇచ్చిన కోణాలకు సంపూరక కోణాలను కనుగొనండి.
(i) 13°
సాధన.
13°లకు ‘సంపూరక కోణం = 180 – 13 = 167°
(ii) 97°
సాధన.
97° లకు సంపూరక కోణం = 180 – 97 = 83°
(iii) a°
సాధన.
a° లకు సంపూరక కోణం = (180 – a°)
(iv) 46°
సాధన.
46°లకు సంపూరక కోణం = 180 – 46 = 134°
ప్రశ్న 3.
ఇచ్చిన కోణాలకు సంయుగ్మ కోణాలను కనుగొనండి.
(i) 74°
సాధన.
74°లకు సంయుగ్మ కోణం = 360 – 74 = 286°
![]()
(ii) 180°
సాధన.
180° లకు సంయుగ్మ కోణం = 360 – 180 = 180°
(iii) m°
సాధన.
m° లకు సంయుగ్మ కోణం = (360 – m)°
(iv) 300°
సాధన.
300° లకు సంయుగ్మ కోణం = 360 – 300 = 60°
[పేజి నెం. 132]
(i) “రెండు అల్పకోణాలు, సంపూరక కోణాల జతను ఏర్పరచ లేవు” అని ఉమేష్ అన్నాడు. మీరు అంగీకరిస్తారా? కారణం తెల్పండి.
సాధన.
“రెండు అల్పకోణాలు, సంపూరక కోణాల జతను ఏర్పరచలేవు” అన్న ఉమేష్ వాదనతో అంగీకరిస్తాను.
కారణం: అల్పకోణము 90° కన్నా తక్కువ. 90° కన్నా తక్కువ అయిన రెండు కోణాల మొత్తం 180° కన్నా తక్కువగా ఉంటుంది. కాబట్టి ఉమేష్ అన్నట్లు “రెండు
అల్పకోణాలు, సంపూరక కోణాల జతను ఏర్పరచలేవు”.
(ii) “పూరక కోణాల జతలో ప్రతికోణం ఎల్లప్పుడూ అల్ప కోణమే” అని లోకేష్ అన్నాడు. మీరు అంగీకరిస్తారా? మీ సమాధానాన్ని సమర్థించండి.
సాధన.
“పూరక కోణాల జతలో ప్రతికోణం ఎల్లప్పుడూ అల్ప కోణమే” అన్న లోకేష్ వాదనతో నేను అంగీకరిస్తాను.
కారణం: పూరక కోణాల జతలోని ప్రతి కోణము అల్పకోణము అయినప్పుడు మాత్రమే వాని మొత్తం 90° అవుతుంది. పూరక కోణాల జతలో ఏదేని కోణం అల్పకోణం కాకపోతే వాని మొత్తం 90° కన్నా ఎక్కువ అవుతుంది. కాబట్టి, లోకేష్ అన్నట్లు “పూరక కోణాల జతలో ప్రతి కోణము ఎల్లప్పుడూ అల్పకోణమే”.
![]()
ఆలోచించండి [పేజి నెం. 138]
ప్రశ్న 1.
పటంలో, ∠AOB మరియు ∠BPC లు ఆసన్న కోణాలు కావు. ఎందుకు ? కారణం తెల్పండి.
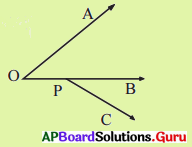
సాధన.
∠AOB మరియు ∠BPCలు ఆసన్న కోణాలు కావు. ఎందుకనగా, రెండు కోణాలకు ఉమ్మడి శీర్షం లేదు.
ప్రశ్న 2.
పటంలో, ∠AOB మరియు ∠COD లకు ఉమ్మడి శీర్షం O. కాని ∠AOB, ∠COD ఆసన్న కోణాలు కావు. ఎందుకు ? కారణం తెల్పండి.
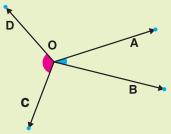
సాధన.
∠AOB మరియు ∠COD లకు ఉమ్మడి శీర్షం ‘O’ ఉన్నప్పటికి అవి ఆసన్న కోణాలు కావు. ఎందుకనగా, ఈ రెండు కోణాలకు ఉమ్మడి భుజం లేదు.
ప్రశ్న 3.
పటంలో, ∠POQ మరియు ∠POR లకు ఉమ్మడి శీర్షం 0 మరియు ఉమ్మడి భుజం OP గా కలవు. కానీ ∠POQ మరియు ∠PORలు ఆసన్నక్ కాలు కావు. ఎందుకు ? కారణం తెల్పండి.
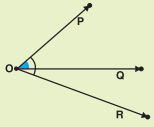
సాధన.
∠POQ మరియు ∠POR లకు ఉమ్మడి శీర్షం ‘O’ మరియు ఉమ్మడి భుజం OP గా కలవు. కాని ఇవి ఆసన్న కోణాలు కావు. ఎందుకనగా ఈ రెండు కోణాలు ఉమ్మడి భుజానికి చెరొక వైపు లేవు.
![]()
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 140]
క్రిందిపటం \(\overleftrightarrow{P R}\) ఒక సరళ రేఖ మరియు సరళ రేఖ \(\overleftrightarrow{P R}\) పై 0 ఒక బిందువు. \(\overleftrightarrow{O Q}\) ఒక కిరణం.
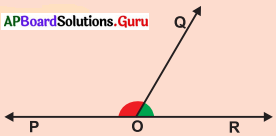
(i) ∠QOR = 50° అయిన ∠POQ విలువ ఎంత ?
సాధన.
∠QOR + ∠POQ = 180° (రేఖీయ ద్వయం)
⇒ 50° + ∠POQ = 180°
⇒ ∠POQ = 180° – 50° = 130°
∴ ∠POQ = 130°
(ii) ∠QOP = 102° అయిన ∠QOR విలువ ఎంత?
సాధన.
∠QOP + ∠QOR = 180° (రేఖీయ ద్వయం)
⇒ 102° + ∠QOR = 180°
⇒ ∠QOR = 180° – 102°
∴ ∠QOR = 78°
అన్వేషిద్దాం [పేజి నెం. 140]
ప్రశ్న 1.
రేఖీయద్వయం ఎల్లప్పుడూ ఆసన్నకోణాలు అవుతాయి. కానీ ఆసన్నకోణాలు ఎల్లప్పుడూ రేఖీయద్వయం కావలసిన అవసరం లేదు. మీరు అంగీకరిస్తారా ? మీ సమాధానాన్ని సమర్థించుటకు ఒక పటాన్ని గీయండి.
సాధన.
అంగీకరిస్తాను.
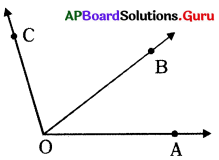
∠AOB, ∠BOC లు ఆసన్న కోణాలు కాని అవి రేఖీయద్వయం కావు.
ప్రశ్న 2.
రెండు కోణాలు 30° మరియు 150°ల మొత్తం 180° కనుక అవి రేఖీయద్వయం అవుతాయి అని మహేష్ చెప్పాడు. దీనిని నీవు అంగీకరిస్తావా ? మీ సమాధానాన్ని సమర్థించండి.
సాధన.
మహేష్ వాదనను అంగీకరించను.
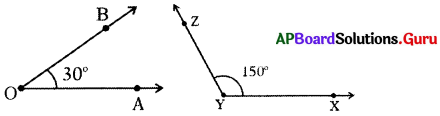
పై పటంలో ∠AOB = 309, ∠XYZ = 150° కాని అవి రేఖీయద్వయం కావు. కావున రెండు కోణాలు 30° మరియు 150°ల మొత్తం 180° కనుక అవి రేఖీయం అవుతాయి అని అంటున్న మహేష్ వాదనను అంగీకరించను.
![]()
ఆలోచించండి [పేజి నెం. 140]
(i) క్రింది పటంలో, \(\overleftrightarrow{A B}\) ఒక సరళరేఖ, సరళరేఖ \(\overleftrightarrow{A B}\) పై
0ఒక బిందువు. \(\overrightarrow{\mathrm{OC}}\) ఒక కిరణం. ∠AOC అంతరంలో బిందువు D ని తీసుకొని, OD కలపండి.
∠AOD + ∠DOC + ∠COB ను కనుగొనండి.
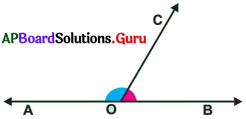
సాధన.
∠AOC మరియు ∠COB లు రేఖీయ జత.
కాని, ∠AOC = ∠AOD + ∠DOC
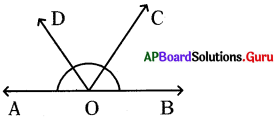
⇒ ∠AOC + ∠COB = 180° (రేఖీయ జత)
⇒ ∠AOD + ∠DOC + ∠COB = 180°
(ii) క్రింది పటంలో AG ఒక సరళరేఖ, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 విలువ కనుగొనండి.
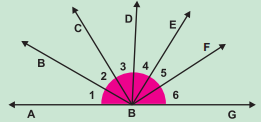
సాధన.
∠AOC మరియు ∠COG లు రేఖీయ జత.
∠AOC + ∠COG = 180° (రేఖీయ జత)
కాని, ∠AOC = ∠AOB + ∠BOC
= ∠1 + ∠2
∠COG = ∠COD + ∠DOE + ∠EOF + ∠FOG
= ∠3 + ∠4 + ∠5 + ∠6 7
⇒ (∠AOB + ∠BOC) + (∠COD + ∠DOE + ∠EOF + ∠FOG) = 180°
⇒ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6
= 180°
ఇవి చేయండి కృత్యిం [పేజి నెం. 144]
ఒక తెల్ల కాగితం తీసుకోండి. ఈ కాగితంపై 3 విభిన్న జతల ఖండన రేఖలను గీయండి. అలా ఏర్పడిన కోణాలను కొలిచి, పట్టికలో నింపండి.
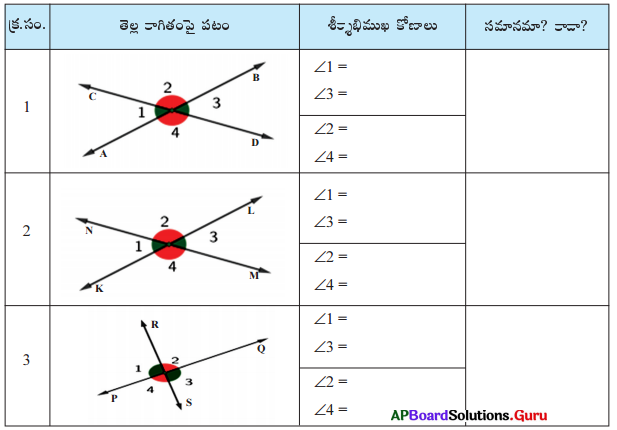
పై పట్టిక నుండి “శీర్షాభిముఖ కోణాలు సమానం” అని గమనించగలరు.
సాధన.
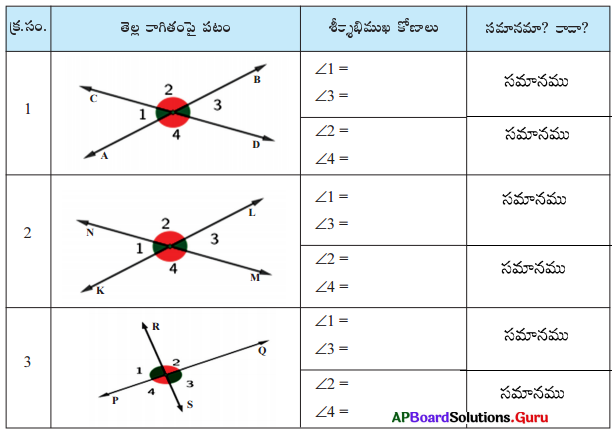
![]()
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 146]
పటంలో మూడు సరళరేఖలు p, q మరియు r లు ఒక బిందువు 0 వద్ద ఖండించుకొనినవి. పటంలో కోణాలను పరిశీలించండి. క్రింది ప్రశ్నలకు సమాధానాలు రాయండి.
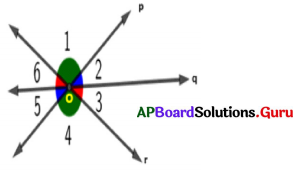
(i) ∠1 కి శీర్షాభిముఖ కోణం ఏది ?
సాధన.
∠1 కి శీర్షాభిముఖ కోణం ∠4.
(ii) ∠6కి శీర్షాభిముఖ కోణం ఏది?
సాధన.
∠6 కి శీర్షాభిముఖ కోణం ∠3.
(iii) ∠2 = 50° అయిన ∠5 విలువ ఎంత ?
సాధన.
∠2 = 50° అయిన ∠5 = 50°. (∠2 మరియు ∠5 లు శీర్షాభిముఖ కోణాలు కావున ∠2 = ∠5)
ఆలోచించండి [పేజి నెం. 150]
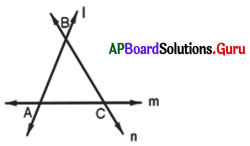
(i) పటంలో సరళరేఖ l మిగిలిన రెండు సరళరేఖలు m, n లను వరుసగా A మరియు B బిందువుల వద్ద ఖండించినది. అందువల్ల l ఒక తిర్యగ్రేఖ అవుతుంది. పటంలో ఇంకా ఏమైనా తిర్యగ్రేఖలు ఉన్నాయా? కారణం తెల్పండి.
సాధన.
m, n లు కూడా తిర్యగ్రేఖలు అవుతాయి.
కారణం: m సరళరేఖ, మిగిలిన రెండు సరళరేఖలు l, nలను A, C అనే బిందువుల వద్ద ఖండించుచున్నది. కావున, m ఒక తిర్యగ్రేఖ అవుతుంది. అలాగే సరళరేఖ n, మిగిలిన రెండు సరళరేఖలు l, m లను B, C బిందువుల వద్ద ఖండించుచున్నది. కావున n ఒక తిర్యగ్రేఖ అవుతుంది.
(ii) ఒక జత సరళరేఖలకు ఎన్ని తిర్యగ్రేఖలను గీయవచ్చు?
సాధన. ఒక జత సరళరేఖలకు అనంత తిర్యగ్రేఖలను గీయ వచ్చును.
![]()
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 152]
పటం (i) మరియు (ii) లను గమనించి, పట్టికను పూరించండి.
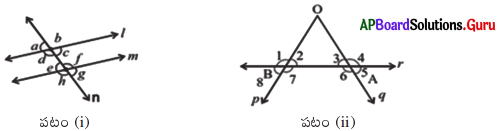
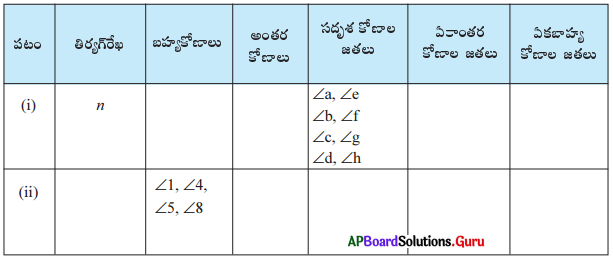
సాధన.
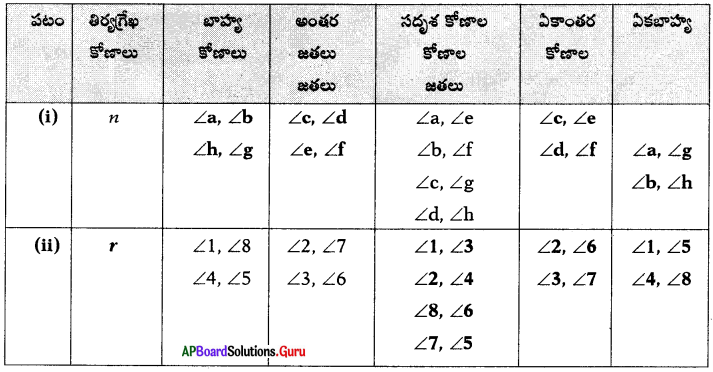
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 156]
పటంలో p || q మరియు t ఒక తిర్యగ్రేఖ.
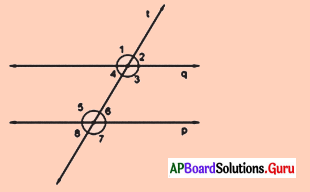
పటంలో కోణాలను పరిశీలించి, క్రింది వానికి జవాబులు రాయండి.
(i) ∠1 = 100° అయిన ∠5 విలువ ఎంత ?
సాధన.
∠1 = 100° అయిన ∠5 = 100° (సదృశ కోణాలు)
(ii) ∠8 = 80° అయిన ∠4 విలువ ఎంత ?
సాధన.
∠8 = 80° అయిన ∠4 = 80° (సదృశ కోణాలు)
(iii) ∠3 = 145° అయిన ∠7 విలువ ఎంత ?
సాధన.
∠3 = 145° అయిన ∠7 = 145° (సదృశ కోణాలు)
(iv) ∠6 = 30° అయిన ∠2 విలువ ఎంత ?
సాధన.
∠6 = 30° అయిన ∠2 = 30° (సదృశ కోణాలు)
ఆలోచించండి [పేజి నెం. 156]
ఒక జత సమాంతర రేఖలను తిర్యగ్రేఖ ఖండించినప్పుడు ఏర్పడే ఏక బాహ్య కోణాల మధ్య గల సంబంధం ఏమిటి?
సాధన.
ఒక జత సమాంతర రేఖలను తిర్యగ్రేఖ ఖండించినపుడు ఏర్పడే ఏక బాహ్య కోణాలు సమానాలు.
![]()
నీ ప్రగతిని సరిచూసుకో, [పేజి నెం. 160]
ప్రశ్న 1.
పటంలో m || n మరియు l ఒక తిర్యగ్రేఖ.
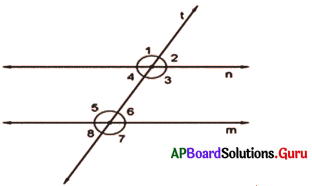
(i) ∠3 = 116° అయిన ∠5 విలువ ఎంత అవుతుంది?
సాధన.
∠3 = 116° అయిన ∠5 = 116° (ఏకాంతర కోణాలు)
(ii) ∠4 = 51° అయిన ∠5 విలువ ఎంత అవుతుంది?
సాధన.
∠4 + ∠5 = 180°
(తిర్యగ్రేఖకు ఒకే వైపు గల అంతరంగా గల కోణము సంపూరకాలు)
⇒ 51° + ∠5 = 180°
⇒ ∠5 = 180° – 51° = 129°
(iii) ∠1 = 123° అయిన ∠7 విలువ ఎంత అవుతుంది?
సాధన.
∠1 = 123° అయిన ∠7 = 123° (సదృశ కోణాలు)
(iv) ∠2 = 66° అయిన ∠7 విలువ ఎంత అవుతుంది?
సాధన.
∠2 = 66° అయిన ∠7 = 114°
(తిర్యగ్రేఖకు ఒకే వైపు గల బాహ్యంగా గల కోణాలు సంపూరకాలు)
∴ ∠2 + ∠7 = 180°
∠7 = 180° – 66° = 114°
ఆలోచించండి [పేజి నెం. 160]
ఒక జత సమాంతర రేఖలను తిర్యగ్రేఖ ఖండించినప్పుడు ఏర్పడే సహబాహ్య కోణాల మధ్య గల సంబంధం ఏమిటి?
సాధన.
ఒక జత సమాంతర రేఖలను తిర్యగ్రేఖ ఖండించినపుడు ఏర్పడే సహబాహ్య కోణాలు సంపూరకాలు.
![]()
ఇవి చేయండి కృత్యం [పేజి నెం. 160]
ఒక తెల్ల కాగితాన్ని తీసుకొనుము. పటం 1 లో చూపిన విధంగా దానిపై సమాంతరంగా లేని రెండు సరళరేఖలు p మరియు q లను గీయండి. వాటిని ఖండించేటట్లు ఒక తిర్యగ్రేఖ r ను గీయండి. అప్పుడు ఏర్పడిన సదృశకోణాలు జతలను కొలిచి పట్టికను పూరించండి.
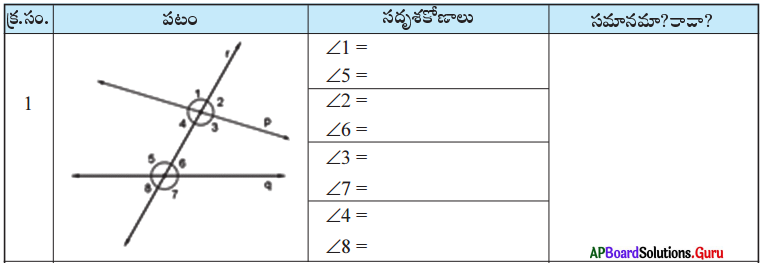
సాధన.
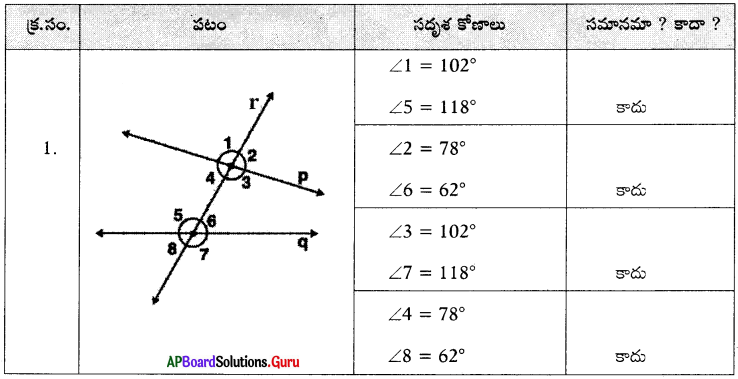
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 162]
పటాన్ని పరిశీలించి, క్రింద ఇచ్చిన ప్రతిదానిలో ఉపయోగించిన న్యాయాన్ని వ్రాయండి.
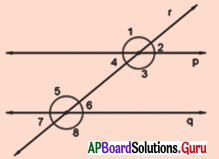
(i) ∠3 = ∠5 అయిన p || q.
సాధన.
ఏకాంతర కోణాల జత సమానము, కనుక ఆ రెండు సరళరేఖలు (p మరియు q) సమాంతరాలు.
(ii) ∠3 + ∠6 = 180° అయిన p || q.
సాధన.
తిర్యగ్రేఖకు ఒకే వైపు గల అంతర కోణాలు సంపూరకాలు. కనుక, ఆ రెండు సరళరేఖలు (p మరియు q) సమాంతరాలు.
![]()
(iii) ∠3 = ∠8 అయిన p || q.
సాధన.
సదృశ కోణాల జత సమానము. కనుక, ఆ రెండు సరళరేఖలు (p మరియు q) సమాంతరాలు.
(iv) p || q అయిన ∠1 = ∠8.
సాధన.
సమాంతర రేఖలను తిర్యగ్రేఖ ఖండించినపుడు ఏర్పడిన ఏక బాహ్య కోణాలు సమానము.
అన్వేషిద్దాం [పేజి నెం. 162]
ప్రశ్న 1.
ఒక జత సరళరేఖలను తిర్యగ్రేఖ ఖండించినపుడు ఏర్పడిన ఏక బాహ్యకోణాల జత సమానం అయిన ఆ రెండు సరళరేఖలు గూర్చి నీవేమి చెప్పగలవు ?
సాధన.
ఆ రెండు సరళరేఖలు సమాంతరాలు.
ప్రశ్న 2.
ఒక జత సరళరేఖలను తిర్యగ్రేఖ ఖండించినపుడు ఏర్పడిన సహబాహ్యకోణాల జత సంపూరకాలు అయినచో ఆ రెండు సరళరేఖలు గూర్చి నీవేమి చెప్పగలవు ?
సాధన.
ఆ రెండు సరళరేఖలు సమాంతరాలు.
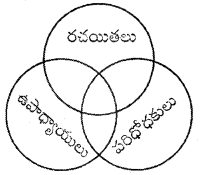
తార్కిక విభాగం , తార్కిక వెన్ చిత్రాలు [పేజి నెం. 170]
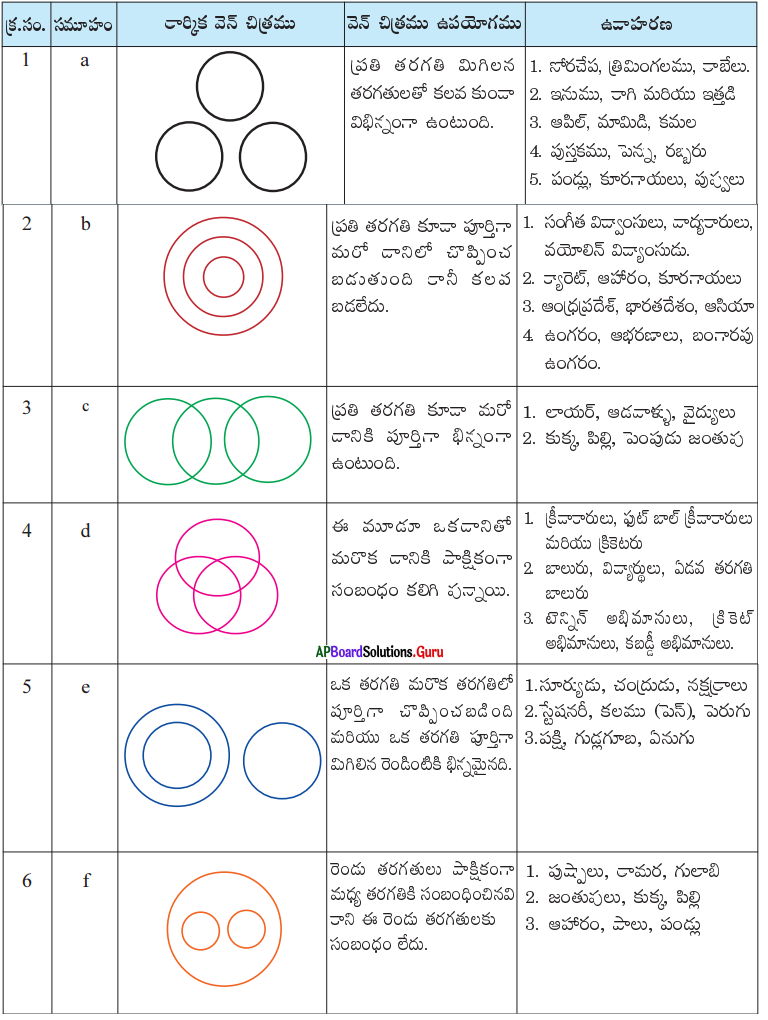
వస్తువుల మధ్య సంబంధాలను లేదా వస్తువుల యొక్క చిన్న సమూహాల మధ్య సంబంధాలను చూపించడానికి ఉపయోగించే వృత్తాలే వెన్ చిత్రం. ఓవర్ ల్యాప్ అయ్యే వృత్తాల లక్షణాలు ఉమ్మడిగా ఉంటూ, ఓవర్ ల్యాప్ కాని వృత్తాలు వాటి లక్షణాలను పంచుకోవు. వెన్ చిత్రాలు మూడు లేదా అంతకంటే ఎక్కువ భావనల మధ్య ఉండే పోలికలు మరియు తేడాలను దృశ్యపరంగా ప్రాతినిధ్యం వహించడానికి సాయపడతాయి
![]()
ఉదాహరణలు
ప్రశ్న 1.
ఇచ్చిన పటంలో ∠B మరియు ∠E లు పూరక కోణాలు అయిన X యొక్క విలువను కనుగొనండి.
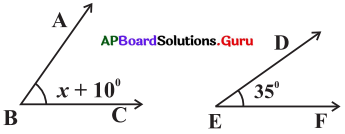
సాధన.
పటం నుండి, ∠B = x + 10° మరియు ∠E = 35°
∠B మరియు ∠E లు పూరక కోణాలు కనుక, ∠B + ∠E = 90°
⇒ x + 10° + 35° = 90°
⇒ x + 45° = 90°
⇒ x = 90°- 45°
∴ x = 45°
ప్రశ్న 2.
సంపూరక కోణాల నిష్పత్తి 4 : 5 అయిన ఆ రెండు కోణాలను కనుగొనండి.
సాధన.
ఇచ్చిన సంపూరక కోణాల నిష్పత్తి = 4 : 5
నిష్పత్తిలో భాగాల యొక్క మొత్తం = 4 + 5 = 9
సంపూరక కోణాల మొత్తం = 180°
మొదటి కోణం = \(\frac{4}{9}\) × 180° = 80°
రెండవ కోణం = \(\frac{5}{9}\) × 180 ° = 100°
ప్రశ్న 3.
ఒకదానితో మరొకటి సమానంగా ఉండే రేఖీయ కోణాల జతను కనుగొనండి.
సాధన.
సమానంగా గల రేఖీయ కోణాల జతను X° మరియు
x° అని అనుకొనుము.
x° + x° = 180°
2x° = 180°
x° = \(\frac{180^{\circ}}{2}\)
x° = 90°
కనుక, ఒక్కొక్క కోణం = 90°
ప్రశ్న 4.
ఇచ్చిన పటంలో \(\overleftrightarrow{P S}\) ఒక సరళరేఖ అయిన x° కనుగొనండి.
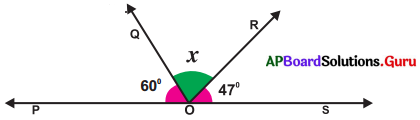
సాధన.
ఇచ్చిన పటం నుండి, ∠POQ = 60°
∠QOR = x°
∠ROS = 47°
కాని, ∠POQ + ∠QOR + ∠ROS = 180°
⇒ 60° + x° + 47° = 180°
⇒ x° + 107° = 180°
⇒ x° = 180° – 107°
∴ x° = 73°
![]()
ప్రశ్న 5.
క్రింది పటాన్ని గమనించి, X, Y మరియు z విలువలను కనుగొనండి.
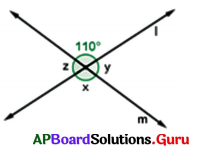
సాధన.
పటం నుండి, x = 110° (శీర్షాభిముఖ కోణాలు సమానం )
y + 110° = 180°
y = 180° – 110° = 70°
z = y
z = 70°
కనుక, x = 110°, y = 70° మరియు z = 70°
ప్రశ్న 6.
ఇచ్చిన పటంలో \(\overrightarrow{\mathbf{A B}}\)||\(\overrightarrow{\mathbf{C D}}\) మరియు \(\overrightarrow{\mathbf{A E}}\) ఒక తిర్యగ్రేఖ. ∠BAC = 120° అయితే X మరియు y లను కనుగొనండి.
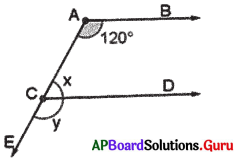
సాధన.
ఇచ్చిన పటంలో \(\overrightarrow{\mathbf{A B}}\)||\(\overrightarrow{\mathbf{C D}}\) మరియు \(\overrightarrow{\mathbf{A E}}\) ఒక తిర్యగ్రేఖ.
∠BAC = 120°
∠ACD = x
∠DCE = y
∠BAC = ∠DCE (సదృశకోణాలు సమానం)
∴ y = 120°
x + y = 180 ° (రేఖీయ ద్వయం సంపూరకాలు)
x + 120° = 180°
x = 180° – 120°
∴ x = 60°
కనుక x = 60°, y = 120°.
![]()
ప్రశ్న 7.
ఇచ్చిన పటంలో, \(\overrightarrow{\mathrm{BA}}\) || \(\overrightarrow{\mathrm{CD}}\) మరియు \(\overrightarrow{\mathrm{BC}}\) ఒక తిర్యగ్రేఖ అయిన X ను కనుగొనండి.
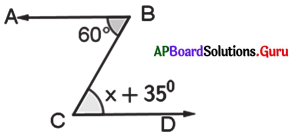
సాధన.
ఇచ్చిన పటంలో, \(\overrightarrow{\mathrm{BA}}\) || \(\overrightarrow{\mathrm{CD}}\) మరియు \(\overrightarrow{\mathrm{BC}}\) ఒక తిర్యగ్రేఖ.
∠C = x + 35° మరియు ∠B = 60°
∠C = ∠B (∵ ఏకాంతర కోణాలు సమానం)
x + 35° = 60°
x = 60° – 35°
∴ x = 25°
ప్రశ్న 8.
పటంలో \(\overrightarrow{\mathrm{MN}}\) || \(\overrightarrow{\mathrm{KL}}\) మరియు \(\overline{\mathrm{MK}}\) ఒక తిర్యగ్రేఖ అయిన X ను కనుక్కోండి.
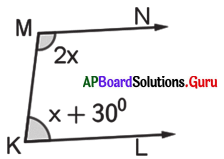
సాధన.
పటంలో \(\overrightarrow{\mathrm{MN}}\) || \(\overrightarrow{\mathrm{KL}}\) మరియు \(\overline{\mathrm{MK}}\) ఒక తిర్యగ్రేఖ.
పటం నుండి, ∠M = 2x మరియు ∠K= x + 30°
∠M + ∠K= 180°
(తిర్యగ్రేఖకు ఒకే వైపున గల అంతర కోణాల జత సంపూరకాలు)
⇒ 2x + x + 30° = 180°
⇒ 3x + 30° = 180°
⇒ 3x = 180° – 30°
⇒ 3x = 150°
⇒ x = \(\frac{150^{\circ}}{3}\)
∴ x = 50°
ప్రశ్న 9.
ఇచ్చిన చిత్రంలో \(\overline{\mathrm{AB}}\)||\(\overline{\mathrm{DE}}\) మరియు వాటి మధ్యలో ఒక బిందువు C. పటాన్ని పరిశీలించి x, y మరియు ∠BCD విలువలను కనుగొనండి.
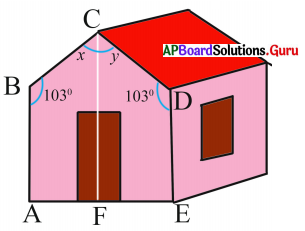
సాధన.
పటం నుండి
ఇచ్చిన చిత్రంలో \(\overline{\mathrm{AB}}\)||\(\overline{\mathrm{DE}}\) మరియు వాటి మధ్యలో ఒక బిందువు C.
\(\overline{\mathrm{AB}}\) కి సమాంతర రేఖ \(\overline{\mathrm{CF}}\) ను C నుండి గీయండి.
\(\overline{\mathrm{AB}}\)||\(\overline{\mathrm{CF}}\) మరియు \(\overline{\mathrm{BC}}\) ఒక తిర్యగ్రేఖ.
x + 103° = 180°
x = 180° – 103°
x = 77°
పటం నుండి,
\(\overline{\mathrm{DE}}\) || \(\overline{\mathrm{CF}}\) మరియు \(\overline{\mathrm{CD}}\) ఒక తిర్యగ్రేఖ.
y + 103° = 180°
y = 180° – 103°
y = 77°
మరియు ∠BCD = x + y
= 77° + 77°
= 154°
![]()
ప్రశ్న 10.
ఇచ్చిన పటంలో m, n లు రెండు సరళరేఖలు. p ఒక తిర్యగ్రేఖ. పటాన్ని పరిశీలించి m || n అవుతుందో, లేదో కనుక్కోండి.
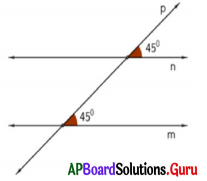
సాధన.
ఇచ్చిన పటంలో ఒక జత సదృశ కోణాలు ఒక్కొక్కటి 45° గా ఇవ్వబడింది. ఇవి సమానాలు. ఒక జత సరళ రేఖలను తిర్యగ్రేఖ ఖండించినపుడు ఏర్పడిన సదృశ కోణాల జత సమానం అయినచో ఆ రెండు సరళరేఖలు సమాంతరంగా ఉంటాయి. కనుక, m || n అవుతుంది.
సాధనా ప్రశ్నలు [పేజి నెం. 174]
పై పట్టికలోని ఏ సమూహం (ఎ, బి, సి, డి, ఇ, ఎఫ్), క్రింద ఇచ్చిన ప్రశ్నలకు చెందినదో సూచించండి.
ప్రశ్న 1.
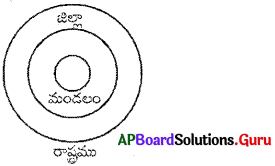
రాష్ట్రము, జిల్లా, మండలం
జవాబు.
సమూహం: బి
వివరణ
ప్రశ్న 2.
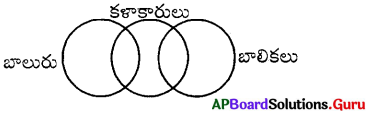
బాలురు, బాలికలు, కళాకారులు
జవాబు.
సమూహం: సి
వివరణ
![]()
ప్రశ్న 3.
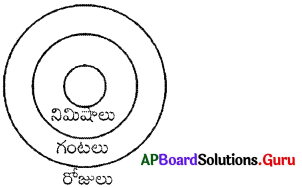
గంటలు, రోజులు, నిమిషాలు
జవాబు.
సమూహం: బి
వివరణ
ప్రశ్న 4.
మహిళలు, ఉపాధ్యాయుడు, వైద్యుడు
జవాబు.
సమూహం: సి
వివరణ

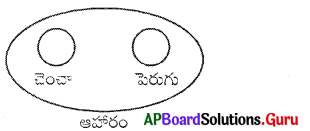
ప్రశ్న 5.
ఆహారము, పెరుగు, చెంచా
జవాబు.
సమూహం: ఎఫ్
వివరణ
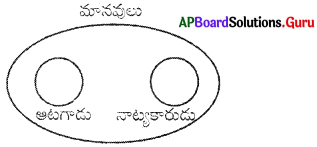
ప్రశ్న 6.
మానవులు, నాట్యకారుడు, ఆటగాడు
జవాబు.
సమూహం: ఎఫ్
వివరణ
ప్రశ్న 7.
భవనము, ఇటుక, వంతెన
జవాబు.
సమూహం: సి
వివరణ
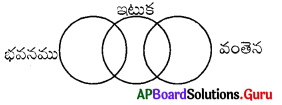
ప్రశ్న 8.
చెట్టు, కొమ్మ, ఆకు
జవాబు.
సమూహం: బీ
వివరణ
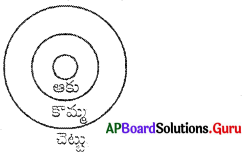
![]()
ప్రశ్న 9.
బంగారం, వెండి, ఆభరణాలు
జవాబు.
సమూహం: ఎఫ్
వివరణ
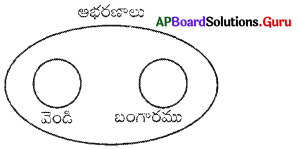
ప్రశ్న 10.
బల్బులు, స్విచ్ లు, ఎలక్ట్రికల్స్
జవాబు.
సమూహం: ఎఫ్
వివరణ
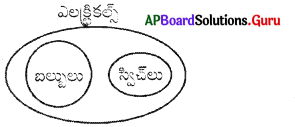
ప్రశ్న 11.
మహిళలు, నిరక్షరాస్యత, పురుషులు
జవాబు.
సమూహం: సి
వివరణ
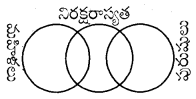
ప్రశ్న 12.
మందులు, మాత్రలు, సిరప్
జవాబు.
సమూహం: ఎఫ్
వివరణ
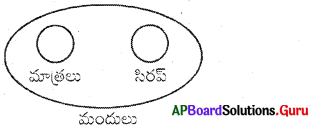
ప్రశ్న 13.
క్యారెట్లు, ఆరెంజ్ లు, కూరగాయలు
జవాబు.
సమూహం: ఇ
వివరణ
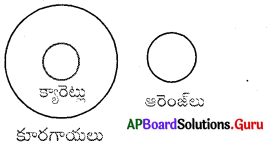
ప్రశ్న 14.
జగ్, పుస్తకం, కుండ
జవాబు.
సమూహం: ఎ
వివరణ
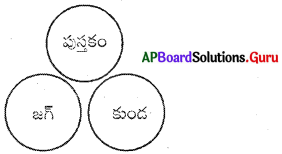
ప్రశ్న 15.
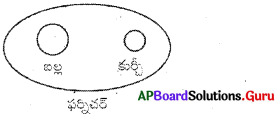
బల్ల, ఫర్నిచర్, కుర్చీ
జవాబు.
సమూహం: ఎఫ్
వివరణ
![]()
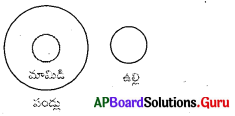
ప్రశ్న 16.
పండ్లు, మామిడి, ఉల్లి
జవాబు.
సమూహం: ఇ
వివరణ
ప్రశ్న 17.
పాఠశాల, ఉపాధ్యాయుడు, విద్యార్థులు
జవాబు.
సమూహం: ఎఫ్
వివరణ

ప్రశ్న 18.
అరటి, చొక్కా, బల్బ్
జవాబు.
సమూహం: ఎ
వివరణ
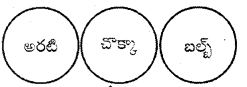
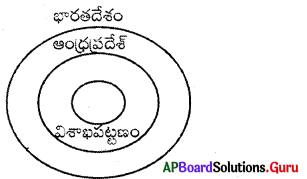
ప్రశ్న 19.
భారతదేశం, ఆంధ్రప్రదేశ్, విశాఖపట్టణం
జవాబు.
సమూహం: బి
వివరణ
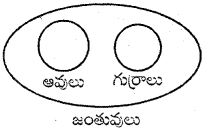
ప్రశ్న 20.
జంతువులు, ఆవులు, గుర్రాలు
జవాబు.
సమూహం: ఎఫ్
వివరణ
![]()
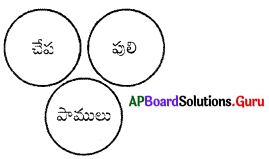
ప్రశ్న 21.
చేప, పులి, పాములు
జవాబు.
సమూహం: ఎ
వివరణ
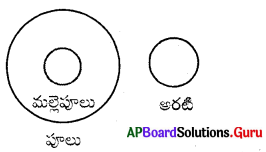
ప్రశ్న 22.
పూలు, మల్లెపూలు, అరటి
జవాబు.
సమూహం: ఇ
వివరణ
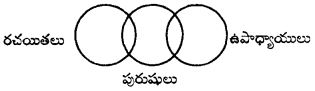
ప్రశ్న 23.
రచయితలు, ఉపాధ్యాయులు, పురుషులు
జవాబు.
సమూహం: సి
వివరణ
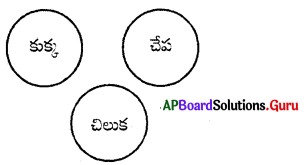
ప్రశ్న 24.
కుక్క, చేప, చిలుక
జవాబు.
సమూహం: ఎ
వివరణ
![]()
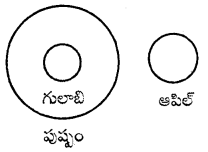
ప్రశ్న 25.
గులాబి, పుష్పం, ఆపిల్
జవాబు.
సమూహం: ఇ
వివరణ
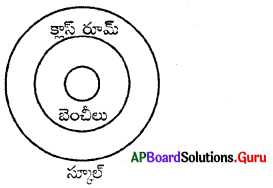
ప్రశ్న 26.
స్కూలు, క్లాస్ రూమ్, బెంచీలు
జవాబు.
సమూహం: బీ
వివరణ
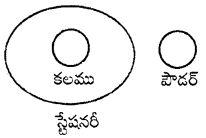
ప్రశ్న 27.
కలము, స్టేషనరీ, పౌడర్
జవాబు.
సమూహం: ఇ
వివరణ
ప్రశ్న 28.
కాకి, పావురం, పక్షులు
జవాబు.
సమూహం: ఎఫ్
వివరణ
ప్రశ్న 29.
క్షీరదాలు, ఏనుగులు, డైనోసార్లు
జవాబు.
సమూహం: ఎఫ్
వివరణ
![]()
ప్రశ్న 30.
రచయితలు, ఉపాధ్యాయులు, పరిశోధకులు
జవాబు.
సమూహం: డి
వివరణ