SCERT AP 7th Class Maths Solutions Pdf Chapter 4 Lines and Angles Ex 4.1 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 4th Lesson Lines and Angles Exercise 4.1
Question 1.
Find which of the following pair of angles are complementary and which are supplementary?
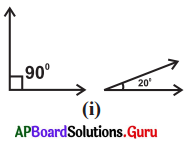
Answer:
90° + 20° = 1 10° ≠ 90° (or) ≠ 180°
So, they are not complementary or not supplementary.
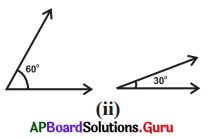
Answer:
6o° + 30° = 90°
So, they are complementary angles.
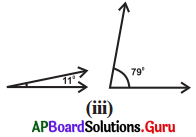
Answer:
11°+ 79° = 90°
So, they arc complementary angles.
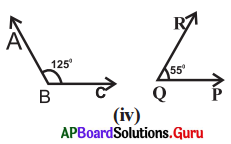
Answer:
125° + 55° = 180°
So, they are supplementary angles.
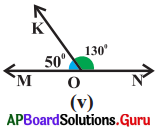
Answer:
50 + 130° = 180°
So, they are supplementary angles.
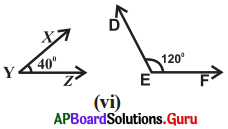
Answer:
40° + 120° = 160° ≠ 90° (or) 180°
So, they are not complementary angles or not supplementary angles.
![]()
Question 2.
If the ratio of two complementary angles is 2:3, then find the two angles.
Answer:
Given the ratio of two complementary angles = 2 : 3 = 2x : 3x
Sum of the complementary angles = 90° So, 2x + 3x = 90°
⇒ 5x = 90°
⇒ \(\frac{5 x}{5}=\frac{90^{\circ}}{5}\)
∴ x = 18°
Then the angles are
2x, 3x = 2(18°), 3(18°) = 36°, 54°
Question 3.
In the figure, ∠A and ∠Q are complementary angles. Find the value of x.
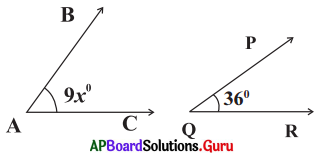
Answer:
Given ∠A = 9x°, ∠Q = 36° and
∠A and ∠Q are complementary angles.
So, ∠A + ∠Q = 90°
⇒ 9x + 36° = 90°
⇒ 9x + 36° – 36° = 90° – 36°
⇒ 9x = 54°
⇒ \(\frac{9 \mathrm{x}}{9}=\frac{54^{\circ}}{9}\)
⇒ x = 6° .
Question 4.
If ∠A and ∠B are conjugate angles and ∠A = ∠B. Find the two angles.
Answer:
Given ∠A and ∠B are conjugate angles and
∠A = ∠B = x°
So, ∠A + ∠B = 360°
⇒ x° + x° – 360°
⇒ 2x° = 360°
⇒ \(\frac{2 x}{2}=\frac{360^{\circ}}{2}\)
⇒ x = 180°
∴ ∠A = ∠B = x° = 180°
Question 5.
Draw a pair of complementary angles and a pair of supplementary angles.
Answer:
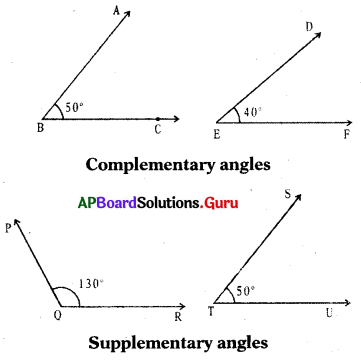
Question 6.
Teacher asked students to draw the complementary angle to the given angle. The students have drawn as follows. Who is correct?
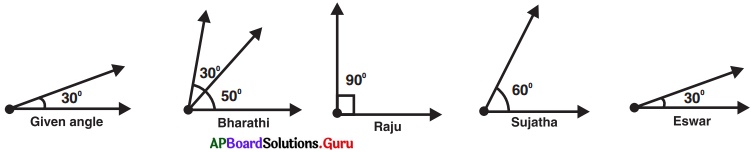
Answer:
Sum of the two angles is 90°, then they are called complementary angles.
Complementary angle of 30° is 60°. So, Sujatha is correct.
Question 7.
In the given figure, ∠B and ∠E are supplementary angles. Find x.
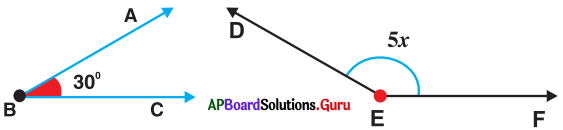
Answer:
Given ∠B and ∠E are supplementary angles.
∠B + ∠E = 180°
⇒ 30° + 5x = 180°
⇒ 30° + 5x – 30° = 180°- 30°
⇒ 5x = 150°
⇒ \(\frac{5 x}{5}=\frac{150^{\circ}}{5}\)
∴ x = 30°
![]()
Question 8.
Ashritha said, “In the pair of supplementary angles, one angle must be obtuse angle.” Do you agree? Give reason.
Answer:
No, two acute angles cannot make supplementary angles. Two right angles (90°) can make supplementary angles. One acute and one obtuse angles can make supplementary angles.
Question 9.
Find the angle which is 40° more than its supplementary angle?
Answer:
Let one angle is x°.
Other angle is (x + 40)°.
Given two angles are supplementary.
So, x + x + 40° = 180°
⇒ 2x + 40° = 180°
⇒ 2x + 40° – 40° = 180° – 40°
⇒ 2x = 140°
⇒ \(\frac{2 x}{2}=\frac{140^{\circ}}{2}\)
Angle x = 70°
Other angle is x + 40° = 70° + 40° = 110°
∴ Angles are 70° and 110°.
Question 10.
Srinu said, “Two obtuse angles cannot be supplementary.” Do you agree? Justify your answer.
Answer:
Yes, sum of two obtuse angles is greater than 180°.