SCERT AP 7th Class Maths Solutions Pdf Chapter 3 Simple Equations InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 3rd Lesson Simple Equations InText Questions
Check your Progress (Page No: 43)
Question 1.
Write simple equations for the following verbal statements.
(i) The sum of five times of x and 3 is 28.
Answer:
Given number = x
Five times of a number = 5 ∙ x
By adding 3 the result = 5x + 3
∴ 5x + 3 = 28
![]()
(ii) Taking away 7 from p gives 21.
Answer:
Given number = p
By subtracting 7 from the number = p – 7
∴ p – 7 = 21
(iii) If you add one third to m, then you get 25.
Answer:
Given number = m
By adding \(\frac{1}{3}\) to m = m + \(\frac{1}{3}\)
then, m + \(\frac{1}{3}\) = 25.
(iv) Sum of angles x, (x + 20) is a straight angle.
Answer:
Given angles are x, x + 20
Sum of angles = x + x + 20
Sum of angles is straight angle (180°).
⇒ x + x + 20 = 180°
∴ 2x + 20 = 180°
(v) Perimeter of a rectangle whose length is 2 cm more than its width is 16 cm.
Answer:
Let width of rectangle = x
Length of rectangle
= 2 more than width = x + 2
Perimeter = 2 (length + width)
= 2(x + 2 + x) = 2(2x + 2)
Given Perimeter = 16 cm
∴ 4x + 4 = 16
Question 2.
Write the following equations in state-ment form.
(i) x + 4 = 9
Answer:
4 is added to a number is 9.
(ii) 2y = 15
Answer:
Two times (twice) a number is 15.
(iii) 3m – 13 = 25
Answer:
13 is taking away from 3 times of m is 25.
(iv) \(\frac{n}{4}\) = 5
Answer:
One fourth of n is 5.
Let’s Do Activity (Page No: 45)
Describe the balances given below in two ways.
(a) Using words (b) Using mathematical symbols.
Answer:
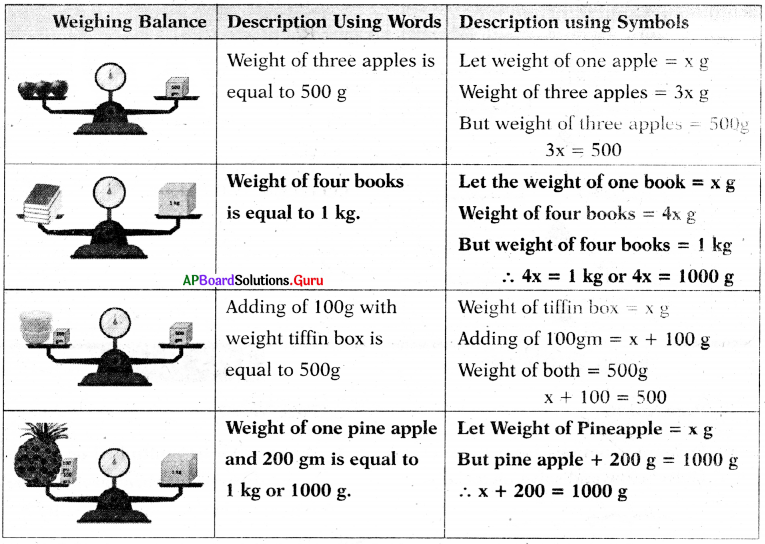
![]()
Lets Explore (Page No: 46)
Develop equations from the pictures given below and solve pictorially.
(i)

Answer:
x + x + x = 5 + 5 + 1 + 1
3x = 12
(ii)

Answer:
y + y + 1 = 5 + 5 + 5
2y + 1 = 15
Let’s Think (Page No: 47)
An equation is multiplied or divided by two different numbers on either side What will happen to the equality?
Answer:
Consider an equation 7x = 14
If we multiply by two different numbers 5 and 8 on either side.
7x × 5 = 14 × 8 ⇒ 35x = 112
So, the equation 7x = 14 is not equal to 35x = 112
(ii) Consider an equation 3x = 15
If we divide by two different numbers 3 and 5 on either side,
3x ÷ 3 = 15 ÷ 5
\(\frac{3 x}{3}\) = \(\frac{15}{5}\) ⇒ x = 3
So, the equation 3x = 15 is not equal to x = 3 either side, the equality will be changes.
Puzzle Time (Page No: 48)
Question 1.
Solve the puzzle using simple equations.
(i)
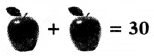
Answer:

![]()
(ii)
![]()
Answer:

(iii)

Answer:

(iv)

Answer:

![]()
Check Your Progress (Page No: 51)
Find three equivalent equations having the same solutions x = – 1.
Answer:

Here x + 5 = 4, 8 – x = 9 and 4x + 5 = 1 are equivalent equations because they have the same solution x = – 1
Puzzle Time (Page No. 52)
Question 1.
Here is a puzzle to reveal the name of great mathematician. Solve the equations and fill the below box with the letter opposite to the solution of the equation and finally it reveals the name of mathematician.
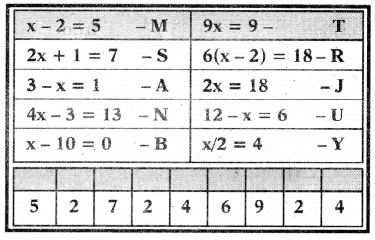
Answer:
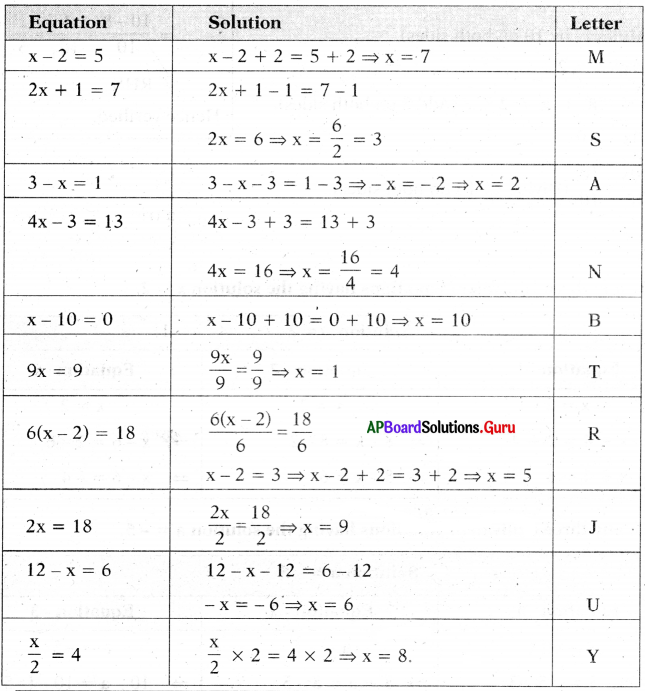

![]()
Check Your Progress (Page No. 53)
Find the value of variable x from the below diagrams.
(i)
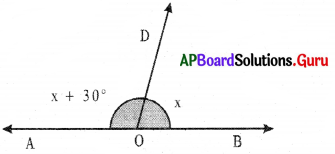
Angle at ‘O’ is straight angle
Answer:
Straight angle = 180°
∠ AOB = 180°
∠ AOB + ∠ BOD = 180°
x + 30° + x = 180°
⇒ 2x + 30° = 180°
⇒ 2x + 30° – 30° – 180°- 30° (Subtract 30° on both sides)
⇒ 2x = 150°
⇒ \(\frac{2 x}{2}\) = \(\frac{150^{\circ}}{2}\) (Divide by 2 on both sides)
∴ x = 75°
(ii)
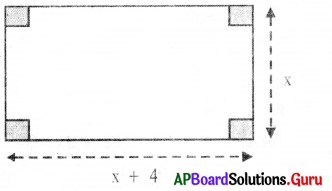
Perimeter = 36 cm
Answer:
Perimeter of rectangle = 36 cm
2(length + breadth) = 36
⇒ 2(x + 4 + x) = 36
⇒ 2(2x + 4) = 36
⇒ \(\frac{2(2 x+4)}{2}\) = \(\frac{36}{2}\) (Divide by 2 on both sides)
⇒ 2x + 4 = 18
⇒ 2x + 4 – 4 = 18 – 4 (Subtract 4 on both sides)
⇒ 2x = 14 .
⇒ \(\frac{2x}{2}\) = \(\frac{14}{2}\) (Divide by 2 on both sides)
∴ x = 7
![]()
Puzzle Time (Page No: 59)
Collect the minimum and maximum temperature (in degrees) of any 5 cities of India of any month and convert the temperature into Fahrenheit and Kelvin Scale.



![]()
Examples
Question 1.
Convert the mathematical statements into simple equations.
(i) 5 added to a number is 9.
Answer:
Let the number = x
By adding 5 to the number = 5 + x
∴ 5 + x = 9
(ii) 4 times a number decreased by 3 is 5.
Answer:
Let the number = m
4 times the number = 4m
By decreasing 3 the result = 4m – 3
∴ 4m – 3 = 5
(iii) The sum of 3 times of n and 7 is 13.
Answer:
Let the number = n
3 times the number = 3n
By adding 7 the result = 3n + 7
∴ 3n + 7 = 13
(iv) Length of rectangle is 3 m more than its breadth and its perimeter is 24 m.
Answer:
Breadth of rectangle = x
Length of rectangle = x + 3
Perimeter = 2(x + 3 + x) = 4x + 6
Given Perimeter = 24 m
∴ 4x + 6 = 24
Question 2.
Convert simple equations into statements.
(i) y – 7 = 11
Answer:
Taking away 7 from ‘y’ is 11.
(ii) 8m = 24
Answer:
8 times of number ‘m’ is 24.
(iii) 2x + 13 = 25
Answer:
If you add 13 to 2 times of number ‘x’ is 25.
(iv) \(\frac{y}{4}\) – 7 = 1
Answer:
7 is subtracted from one fourth of y is 1.
![]()
Question 3.
Check whether the value given in the brackets is a solution to the given equation or not.
2k – 11 = 5 (k = 7)
Answer:
When k = 7
LHS: 2k – 11 = 2(7) – 11 = 14 – 11 = 3
RHS: 5
Here LHS ≠ RHS,
So k = 7 is not a solution.
Question 4.
Solve 6n – 1 = 29 trial and error method.
Answer:
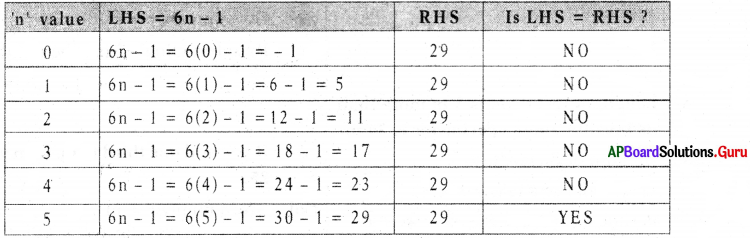
For n = 5, LHS = RHS. So, n = 5 is the solution of given equation.
Question 5.
Solve x + 5 = 8 by using common balance idea.
Answer:

![]()
Question 6.
Solve 2x – 5 = 9 pictorially.
Answer:

Question 7.
Solve: 3k + 4 = 28
Answer:
3k + 4 = 28
⇒ 3k + 4 – 4 = 28 – 4 (Add both sides ‘- 4’)
⇒ 3k = 24
⇒ \(\frac{3 \mathrm{k}}{3}\) = \(\frac{24}{3}\) (Divide both sides by ‘3’)
⇒ k = 8
Check: Substitute k = 8 in the given equation.
LHS = 3k + 4
= 3(8) + 4
= 24 + 4 = 28 = RHS
Hence verified.
Question 8.
Solve: – 4(x – 1) = 16
Answer:
– 4(x – 1) = 16
⇒ 4x + 4 = 16 (Distributive property)
⇒ – 4x + 4 – 4 = 16 – 4 (Subtract both sides ‘4’)
⇒ – 4x = 12
⇒ (- 4x) × (- 1) = 12 × (- 1)
(Multiply with ‘- 1 ‘on both sides)
⇒ 4x = – 12
⇒ \(\frac{4 x}{4}\) = \(\frac{-12}{4}\) (Divide both sides by ‘4’)
⇒ x = – 3
Check: Substitute x = – 3 in the given equation.
LHS = – 4(x – 1)
= – 4(- 3 – 1)
= – 4 (- 4)
= 16
= RHS
Hence verified.
![]()
Question 9.
Solve: 2(b + 3) + 13 = 27
Answer:
2(b + 3) + 13 = 27
⇒ 2b + 6 + 13 = 27 (distributive law)
⇒ 2b + 19 = 27
⇒ 2b = 27 – 19 (∵+ 19 transposed and becomes – 19)
⇒ 2b = 8
⇒ b = \(\frac{8}{2}\) (∵ × 2 transposed and becomes ÷ 2)
⇒ b = 4
Check:
Substitute b = 4
LHS = 2(b + 3) + 13
= 2(4 + 3) + 13
= 2(7) + 13
= 14 + 13
= 27 = RHS
Hence verified.
Question 10.
Solve : 5(x + 1) – 2(x – 7) = 13
Answer:
5(x + 1) – 2(x – 7) = 13
⇒ 5x + 5 – 2x + 14 = 13 (distributive law)
⇒ (5x – 2x) + (5 + 14) = 13 (regrouping like terms)
⇒ 3x +19 = 13
⇒ 3x = 13 – 19 (∵ +19 transposed arid becomes
⇒ 3x = – 6
⇒ x = \(\frac{-6}{3}\) (∵ × 3 transposed and becomes ÷ 3)
⇒ x = – 2
Question 11.
Solve: 12 = 13 + 7 (y-6)
Answer:
12 = 13 + 7 (y – 6)
An equation remains the same,
when LHS, RHS are interchanged.
⇒ 13 + 7(y – 6) = 12 .
⇒ 3 + 7y – 42 = 12 (distributive law)
⇒ 7y – 29 = 12
⇒ 7y = 12 + 29 (∵ – 29 transposed and becomes + 29)
⇒ 7y = 41
⇒ y = \(\frac{41}{7}\) (∵ × 7 transposed and becomes ÷ 7)
Check:
Substitute y = \(\frac{41}{7}\)
RHS = 13 + 7(y – 6)
= 13 + 7(\(\frac{41}{7}\) – 6)
= 13 + 7\(\left(\frac{41-42}{7}\right)\)
= 13 + 7\(\left(\frac{-1}{7}\right)\)
= 13 – 1
= 12 = LHS
Hence verified.
![]()
Question 12.
Solve \(\frac{m}{2}-\frac{2 m}{7}-\frac{m}{10}=\frac{8}{5}\)
Answer:

Check:
Substitute m = 14
LHS = \(\frac{\mathrm{m}}{2}-\frac{2 \mathrm{~m}}{7}-\frac{\mathrm{m}}{10}\)
= 7 – 4 – \(\frac{7}{5}\)
= 3 – \(\frac{7}{5}\)
= \(\frac{15-7}{5}\)
= \(\frac{8}{5}\)
= RHS
Hence verified.
Question 13.
Find the value of variable ‘x’ from the following.
(i) x + 20% of x = 60
Answer:
x + 20% of x = 60
⇒ x + \(\frac{20 x}{100}\) = 60
⇒ x + \(\frac{x}{5}\) = 60
⇒ \(\frac{6x}{5}\) = 60
⇒ 6x = 60 × 5
⇒ x = \(\frac{(60 \times 5)}{6}\)
⇒ x = 50
(ii) If two numbers are in the ratio 2 : 3 and their difference is 5, then find largest number.
Answer:
Let largest number = 3x and smallest number = 2x
Difference = 3x – 2x = x
But as per the problem difference = 5
⇒ x = 5
∴ Largest number = 3x = 3 × 5 = 15
(iii) Find the value of x in the following picture.
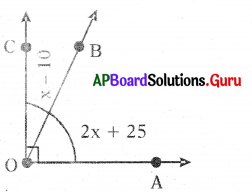
Answer:
Sum of two angles is 90
2x + 25 + x – 10 = 90
⇒ 3x + 15 = 90
⇒ 3x = 90 – 15
⇒ 3x = 75
⇒ x = \(\frac{75}{3}\)
⇒ x = 25
![]()
(iv) If the perimeter of the following tri-angle is 15 cm, then find the value of x.
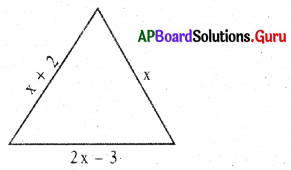
Answer:
Perimeter of a triangle = 15 cm
Perimeter = x + x + 2 + 2x – 3 = 4x – 1
∴ 4x – 1 = 15
⇒ 4x = 15 + 1
⇒ 4x = 16
⇒ x = 4
Question 14.
Find two consecutive natural numbers whose sum is 125.
Answer:
Let the number = x
Consecutive number of x = x + 1
Given that, x + (x + 1) = 125
⇒ 2x + 1 = 125
⇒ 2x = 125 – 1
⇒ 2x = 124
⇒ x = \(\frac{124}{2}\)
x = 62 and x + 1 = 62 + 1 = 63
∴ Required numbers are 62 and 63.
Check:
Numbers: 62, 63
Sum = 62 + 63 = 125
Hence verified.
Question 15.
The sum of two numbers is 35. One of the numbers exceeds the other by 7. Find the numbers.
Answer:
Let the first number = x
Then the second number = x + 7 (exceeds first number by 7)
Sum of two numbers = 35
According to problem, x + x + 7 = 35
⇒ 2x + 7 = 35
⇒ 2x = 35 – 7
⇒ 2x = 28
⇒ x = \(\frac{28}{2}\)
⇒ x = 14
x + 7 = 14 + 7 = 21
∴ The two numbers are 14 and 21
Check:
Numbers: 14, 21
Sum = 14 + 21
= 35
Hence verified.
![]()
Question 16.
A person has ₹ 1400 in denominations of ₹20, ₹10 and ₹5 notes. The number of notes in each denomination is equal, then find the number of notes of each denomination ?

Answer:
Let the number of notes in each denomination be x.
₹20 denomination amount = 20x
₹10 denomination amount = 10x
₹5 denomination amount = 5x
Total amount = ₹ 1400
⇒ 20x + 10x + 5x = 1400
⇒ 35x = 1400
⇒ x = \(\frac{1400}{35}\)
⇒ x = 40
∴ Number of notes in each denomination is 40.
Check:
Number of notes = 40
Amount = (20 × 40 + 10 × 40 + 5 × 40)
= 800 + 400 + 200
= ₹ 1400
Hence Verified.
Question 17.
The length of a rectangle is five meters more than twice of its breadth. If the perimeter is 148 meter, then find the length and breadth of the rectangle.
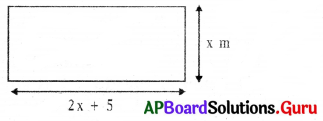
Answer:
Let the breadth of the rectangle = x,
length of a rectangle is five more than twice of its breadth.
Then, length of the rectangle = 2x + 5
Perimeter of the rectangle = 148m
2 (Length + Breadth) = 148
⇒ 2(2x + 5 + x) = 148
⇒ 2(3x + 5) = 148
⇒ 6x + 10 = 148
⇒ 6x = 148 – 10
⇒ 6x = 138
⇒ x = \(\frac{138}{6}\)
⇒ x = 23
∴ Breadth of rectangle = 23 m
Length of the rectangle = 2x + 5 = (2 × 23) + 5
= 46 + 5 = 51 m
Check:
Length = 51 m, Breadth = 23 m
Perimeter = 2(l + b)
= 2(51 + 23)
= 2(74)
= 148 m
Hence Verified.
![]()
Question 18.
On his birthday Yakshith’s grand father has given ₹ 2000. He used some amount for purchasing books for needy children and thrice of that amount for purchasing food items for orphanage children and the remaining ₹ 200 used for purchasing chocolates . for his friends. Find the amount spent for purchasing books and food items for orphanage children.
Answer:
Let the amount spent for purchasing books for needy children = ₹ x
Amount spent for purchasing food items for orphanage children = ₹ 3x
Amount spent for purchasing chocolates for friends = ₹ 200
Total amount spent = ₹ 2000
⇒ x + 3x + 200 = 2000
⇒ 4x + 200 = 2000
⇒ 4x = 2000 – 200
⇒ 4x = 1800
⇒ x = \(\frac{1800}{4}\)
⇒ x = 450
∴ Amount spent for purchasing books for needy children = ₹ 450
Amount spent for purchasing food items for orphanage children = ₹ 3x
= 3 × 450 = ₹ 1350
Check:
Amount = ₹ 450 + ₹ 1350 + ₹ 200
= ₹ 2000
Hence Verified.
Question 19.
A school bus starts with full strength of 40 students. It drops some students at the first bus stop. At the second bus stop, twice the number of students get down from the bus. 8 students get down at the third bus stop and the number of students remaining in the bus is only 5. How many students got down at the first stop and second stop?

Answer:
Let us take the number of students get down at first stop = x
No.of students get down at the second bus stop = 2x
No. of students get down at the third bus stop = 8
Remaining students in the bus = 5
⇒ x + 2x +8 + 5 = 40
⇒ 3x + 13 = 40
⇒ 3x = 40 – 13
⇒ 3x = 27
⇒ x = \(\frac{27}{3}\)
⇒ x = 9
∴ The number of students got down in the first bus stop = 9.
No. of students got down in second stop = 2x = 2 × 9 = 18.
![]()
Practice Questions (Page No: 62)
In the questions given below, equations have become wrong due to wrong order of signs (+, -, ×, ÷, =). Choose the correct order of signs from the alternatives given under each question so that the equation becomes right.
Question 1.
7 + 2 = 2 × 3
(a) = × +
(b) = + ×
(c) = + ÷
(d) + × =
Answer:
(a) = × +
Explaination
Given 7 + 2 = 2 × 3 ,
⇒ 7 = 2 × 2 + 3
⇒ 7 = 4 + 3
∴ 7 = 7
Question 2.
7 + 2 × 6 = 20
(a) = × +
(b) × – =
(c) × + =
(d) ÷ + =
Answer:
(c) × + =
Explaination:
Given 7 + 2 × 6 = 20
⇒ 7 × 2 + 6 = 20
⇒ 14 + 6 = 20
∴ 20 = 20
![]()
Question 3.
15 ÷ 5 = 2 × 1
(a) ÷ × =
(b) ÷ = ×
(c) × = +
(d) ÷ = +
Answer:
(d) ÷ = +
Explaination:
Given 15 ÷ 5 = 2 × 1
⇒ 15 ÷ 5 = 2 + 1
∴ 3 = 3
Question 4.
6 = 3 – 6 ÷ 12
(a) = × +
(b) ÷ = ×
(c) + = –
(d) ÷ × =
Sol.
(d) ÷ × =
Explaination:
Given 6 = 3 – 6 ÷ 12
⇒ 6 ÷ 3 × 6 =12
⇒ 2 × 6 = 12
∴ 12 = 12
Question 5.
3 + 1 ÷ 4 = 16
(a) – = ×
(b) × + =
(c) + × =
(d) = × +
Answer:
(c) + × =
Explaination:
Given 3 + 1 ÷ 4 = 16
⇒3 + 1 × 4 = 16
⇒ 4 × 4 = 16
∴ 16 = 16
![]()
Question 6.
8 ÷ 4 = 2 + 1
(a) ÷ = +
(b) ÷ = ×
(c) ÷ × =
(d) = ÷ ×
Answer:
(b) ÷ = ×
Explaination:
Given 8 ÷ 4 = 2 + 1
⇒ 8 ÷ 4 = 2 × 1
∴ 2 = 2
Question 7.
2 × 2 + 2 = 2
(a) × ÷ =
(b) × = ÷
(c) + × =
(d) × + =
Answer:
(a) × ÷ =
Explaination:
Given 2 × 2 + 2 = 2
⇒ 2 × 2 ÷ 2 = 2
⇒ 2 × 1 = 2
∴ 2 = 2
Question 8.
5 – 6 + 8 = 3
(a) + – =
(b) + = –
(c) – = ×
(d) ÷ × =
Answer:
(a) + – =
Explaination:
Given 5 – 6 + 8 = 3
⇒ 5 + 6 – 8 = 3
⇒ 11 – 8 = 3
∴ 3 = 3
![]()
Question 9.
8 ÷ 2 = 2 × 8
(a) + – =
(b) + ×
(c) ÷ = ×
(d) × = ÷
Answer:
(b) + ×
Explaination:
Given 8 ÷ 2 = 2 × 8
⇒ 8 ÷ 2 × 2 = 8
⇒ 4 × 2 – 8
∴8 = 8
Question 10.
3 = 3 – 7 + 0
(a) – + =
(b) + × =
(c) – × =
(d) = × –
Answer:
(c) – × =
Explaination:
Given 3 = 3 – 7 + 0
⇒ 3 – 3 × 7 = 0
⇒ 0 × 7 = 0
∴ 0 = 0