SCERT AP 7th Class Maths Solutions Pdf Chapter 3 Simple Equations Ex 3.3 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 3rd Lesson Simple Equations Exercise 3.3
Question 1.
Solve the following equations and check the result.
(i) 5x – 17 = 18
Answer:
Given 5x – 17 = 18
⇒ 5x – 17 + 17 = 18 + 17 (Add 17 on both sides)
⇒ 5x = 35
⇒ \(\frac{5 x}{5}\) = \(\frac{35}{5}\) (Divide by 5 on both sides)
⇒ x = 7
Check:
Substitute x = 7 in 5x – 17 = 18
LHS = 5x – 17
= 5(7) – 17
= 35 – 17 = 18 = RHS
Hence verified.
![]()
(ii) 29 – 7y = 1
Answer:
Given 29 – 7y = 1
⇒ 29 – 7y – 29 = 1 – 29 (Subtract 29 on both sides)
⇒ – 7y = -28 .
⇒ \(\frac{-7 y}{-7}\) = \(\frac{-28}{-7}\) (Divide by – 7 on both sides)
⇒ y = 4
Check:
Substitute y = 4 in
29 – 7y = 1
LHS = 29 – 7y
= 29 – 7(4)
= 29 – 28 = 1 = RHS
Hence verified.
(iii) a – 2.3 = 1.5
Answer:
Given a – 2.3 = 1.5
⇒ a – 2.3 + 2.3 = 1.5 + 2.3 (Add 2.3 ort both sides)
⇒ a = 3.8
Check:
Substitute a = 3.8 in a – 2.3 =1.5
LHS = a – 2.3
= 3.8 – 2.3
= 1.5 = RHS
Hence verified.
(iv) b + 3\(\frac{1}{2}\) = \(\frac{7}{4}\)
Answer:

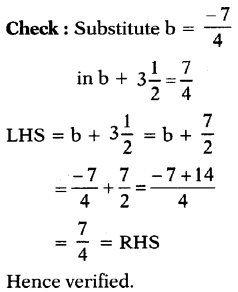
![]()
(v) \(\frac{7 p}{10}\) + 9 = 15
Answer:

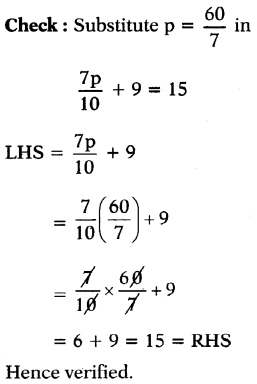
![]()
(vi) 6(q – 5) = 42.
Answer:
Given 6(q – 5) = 42
⇒ \(\frac{6(q-5)}{6}\) = \(\frac{42}{6}\) (Divide by 6 on both sides)
⇒ q – 5 = 7
⇒ q – 5 + 5 = 7 + 5 (Add 5 on both sides)
⇒ q = 12
Check:
Substitute q = 12 in
6(q – 5) = 42
LHS = 6(q – 5)
= 6(12 – 5)
= 6(7) = 42 = RHS
Hence verified.
(vii) – 3(m + 5) + 1 = 13
Answer:
Given – 3(m + 5)4-1 = 13
⇒ – 3(m + 5)+ 1 – 1 = 13 – 1 (Subtract 1 on both sides)
⇒ – 3(m + 5) = 12
⇒ \(\frac{-3(m+5)}{-3}\) = \(\frac{12}{-3}\) (Divide by – 3 on both sides)
⇒ m + 5 = – 4
⇒ m + 5 – 5 = – 4 – 5 (Subtract 5 on both sides)
⇒ m = – 9
Check:
Substitute m = – 9 in – 3(m + 5) + 1 = 13
LHS = – 3(m + 5) + 1
= – 3(- 9 + 5) + 1 = (- 3 × – 4) + 1
= + 12 + 1 = 13 = RHS
Hence verified.
![]()
(viii) \(\frac{n}{2}+\frac{n}{3}+\frac{n}{5}\) = 31
Answer:

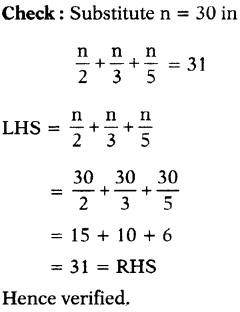
Question 2.
Solve the following equations and check the result.
(i) 3(p – 7) – 4 = 5
Answer:
Given 3(p – 7) – 4 = 5
⇒ 3(p – 7) – 4 + 4 = 5 + 4 (Add 4 on both sides)
⇒ 3(p – 7) = 9
⇒ \(\frac{3(p-7)}{3}\) = \(\frac{9}{3}\) (Divide by 3 on both sides)
⇒ p – 7 = 3
⇒ p – 7 + 7 = 3 + 7 (Add 7 on both sides)
⇒ p = 10
Check:
Substitute p = 10 in
3(p – 7) – 4 = 5
LHS = 3(p – 7) – 4.
= 3(10 – 7) – 4.
= 3 × 3 – 4
= 9 – 4 = 5 = RHS
Hence verified.
(ii) 5(q – 3) – 3(q – 2) = 0
Answer:
Given 5(q – 3) – 3(q – 2) = 0
⇒ 5q – 15 – 3q + 6 = 0 (Distributive property)
⇒ 2q – 9 = 0 .
⇒ 2q – 9 + 9 = 0 + 9 (Add 9 on both sides)
⇒ 2q = 9
⇒ \(\frac{2 \mathrm{q}}{2}\) = \(\frac{9}{2}\) (Divide by 2 on both sides)
⇒ q = \(\frac{9}{2}\)
Check : Substitute q = \(\frac{9}{2}\) in
5(q – 3) – 3(q – 2) = 0
LHS = 5(q – 3) – 3(q – 2)
= 5\(\left(\frac{9}{2}-3\right)\) – 3\(\left(\frac{9}{2}-2\right)\)
= 5\(\left(\frac{9-6}{2}\right)\) – 3\(\left(\frac{9-4}{2}\right)\)
= 5 × \(\frac{3}{2}\) – 3 × \(\frac{5}{2}\)
= \(\frac{15}{2}-\frac{15}{2}\) = 0 = RHS
Hence verified.
![]()
(iii) 4x – 0.3x – 1.2 = 0.6
Answer:
Given 0.4x – 0.3x – 1.2 = 0.6
⇒ 0.1 x – 1.2 = 0.6
⇒ 0.1 x – 1.2 + 1.2 = 0.6 + 1.2 (Add 1.2 on both sides)
⇒ 0.1 x = 1.8
⇒ \(\frac{1 \mathrm{x}}{10}\) = \(\frac{18}{10}\)
![]()
(Multiply by 10 on both sides)
⇒ x = 18
Check:
Substitute x = 18 in
0.4x – 0.3x – 1.2 = 0.6
LHS = 0.4x – 0.3x – 1.2
= 0.4(18) – 0.3(18) – 1.2
= 7.2 – 5.4 – 1.2
= 7.2 – 6.6 = 0.6 = RHS
Hence verified.
(iv) 4(3y + 4) = 7.6
Answer:
Given 4(3y + 4) = 7.6.
⇒ \(\frac{4(3 y+4)}{4}\) = \(\frac{7.6}{4}\) (Divide by 4 on both sides)
⇒ 3y + 4 = 1.9
⇒3y + 4 – 4= 1.9 – 4 (Subtract 4 on both sides)
⇒ 3y = – 2.1
⇒ \(\frac{3 y}{3}\) = – \(\frac{2.1}{3}\) (Divide by 3 on both sides)
⇒ y = – 0.7
Check:
Substitute y = – 0.7 in
4(3y + 4) = 7.6
LHS = 4(3y + 4)
= 4[3 (- 0.7) + 4]
= 4[- 2.1 + 4]
= 4 × 1.9 = 7.6 = RHS
Hence verified.
(v) 20 – (2r – 5) = 25
Answer:
Given 20 – (2r – 5) = 25
![]()
(Subtract 20 on both sides)
⇒ – (2r – 5) = 5
⇒ – (2r -5) × – 1 = 5 × – 1
(Multiply by – 1 on both sides)
⇒ 2r – 5 = 5
⇒ 2r – 5 + 5= – 5 + 5 (Add 5 on both sides)
⇒ 2r = 0
⇒ \(\frac{2 \mathrm{r}}{2}\) = \(\frac{0}{2}\) (Divide by 2 on both sides)
⇒ r = 0
Check:
Substitute r = 0 in
20 – (2r – 5) = 25
LHS = 20 – (2r – 5)
= 20 – [2(0) – 5]
= 20 – [0 – 5]
= 20 – (- 5)
= 20 + 5 = 25 = RHS
Hence verified.
![]()
(vi) 3(5 – t) – 2(t – 2) = – 1
Answer:
Given 3(5 – t) – 2(t – 2) = – 1
⇒ 15 – 3t – 2t + 4 .= – 1 (Distributive property)
⇒ 19 – 5t = – 1
![]()
(Subtract 19 on both sides)
⇒ – 5t = – 20
⇒ \(\frac{-5 t}{-5}\) = \(\frac{-20}{-5}\) (Divide by – 5 on both sides)
⇒ t = 4
Check:
Substitute t = 4 in
3(5 -1) – 2(t – 2) = – 1
LHS = 3(5 – t) – 2(t – 2)
= 3(5 – 4) – 2(4 – 2)
= 3(1) – 2(2)
= 3 – 4 = – 1 = RHS
Hence verified.
(vii) 3(2k + 1) – 2(k – 5) – 5(5 – 2k) = 16
Answer:
Given 3(2k + 1) – 2(k T 5) – 5(5 – 2k) = 16
⇒ 6k + 3-2k + 10-25 + 10k = 16 (Distributive property)
⇒ 14k – 12 = 16
⇒ 14k – 12 + 12 – 16 + 12 (Add 12 on both sides)
⇒ 14k = 28
⇒ \(\frac{14 \mathrm{k}}{14}\) = \(\frac{28}{14}\) (Divide by 14 on both sides)
⇒ k = 2
Check:
Substitute k = 2 in
3(2k + 1) – 2(k – 5) – 5(5 – 2k) = 16
LHS = 3(2k + 1) – 2(k – 5) – 5(5 – 2k)
= 3[2 × 2 + 1] – 2[2 – 5] – 5[5 – 2 × 2]
= 3[4 + 1] – 2(- 3) – 5(5 – 4)
= 15 + 6 – 5 – 16 = RHS
Hence verified.
![]()
(viii) \(\frac{3 \mathrm{~m}}{4}\) – 5m – \(\frac{3}{4}\)
Answer:
 ⇒ – 17m – 3 = 48
⇒ – 17m – 3 = 48
⇒ – 17m – 3 + 3 =48 + 3 (Add 3 on both sides)
⇒ – 17m = 51
⇒ \(\frac{-17 \mathrm{~m}}{-17}\) = \(\frac{51}{-17}\) (Divide by – 17 on both sides)
⇒ m = – 3
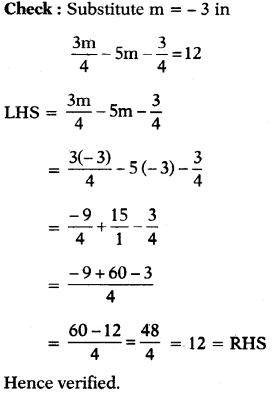
(ix) \(\frac{4 n}{5}+\frac{n}{4}-\frac{n}{2}=\frac{11}{10}\)
Answer:


![]()
(x) \(\frac{x}{2}-\frac{4}{5}+\frac{x}{5}+\frac{3 x}{10}=\frac{1}{5}\)
Answer:

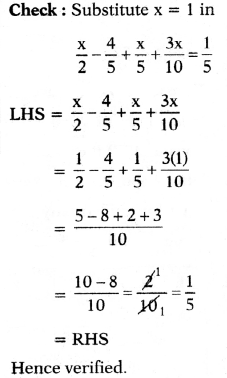
![]()
Question 3.
Write any three equivalent equations having the solution x = 2.
Answer:

Question 4.
Write any three equivalent equations having the solution a = – 5.
Answer:
