AP State Syllabus AP Board 7th Class Maths Solutions Chapter 13 Area and Perimeter InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 13th Lesson Area and Perimeter InText Questions
![]()
Try This
Question 1.
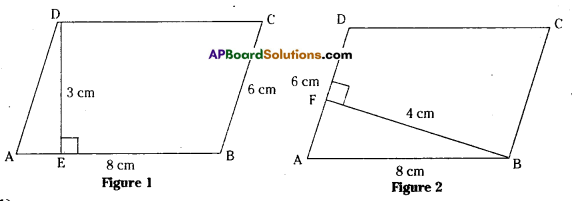
ABCD is a parallelogram with sides 8 cm and 6 cm. In Figure 1, what is the base of the parallelogram? What is the height? What is the area of the parallelogram? In Figure 2, what is the base of the parallelogram? What is the height? What is the area of the parallelogram? Is the area of Figure 1 and Figure 2 the same ? (Page No. 248)
Solution:
In fig (1)
Base of the parallelogram ABCD is 8cm.
Side of the parallelogram ABCD is 6cm.
Height of the parallelogram ABCD is 3cm.
Area of the parallelogram ABCD = base x height = 8×3 = 24cm2
In fig (2)
Base of the parallelogram = 6cm
Side of the.parallelogram = 8cm
Height of the parallelogram = 4cm
Area of the parallelogram = base x height = 6×4 = 24cm2
Yes. Areas of fig (1) & fig (2) are equal.
![]()
Do This
Question 1.
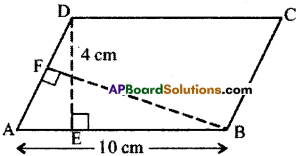
In parallelogram ABCD, AB = 10 cm and DE = 4cm. Find (i) the area of ABCD ii) the length of BF, if AD = 6cm (Page No. 248)
Solution:
Given AB = 10 cm, DE = 4 cm
Area of parallelogram ABCD = Base x Height
= 10 x 4 = 40 cm2
Also area of parallelogram ABCD = Base x Height
40 = AD x BF
40 = 6 x BF
BF = \(\frac{40}{6}=\frac{20}{3}=6 \frac{2}{3}\)= 6.6cm
Do This
Question 1.
Carefully study the following parallelogram. (Page No. 248)
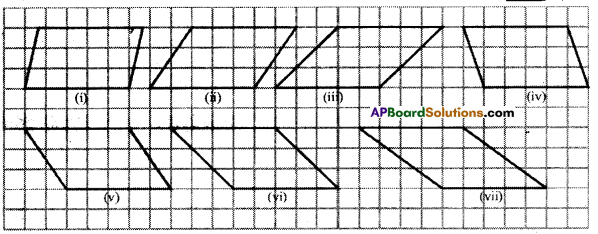
i) Find the area of the each parallelogram by counting the squares enclosed in it. For counting incomplete squares check whether two incomplete squares make a complete square in each parallelogram. Complete the following table accordingly.
Solution:
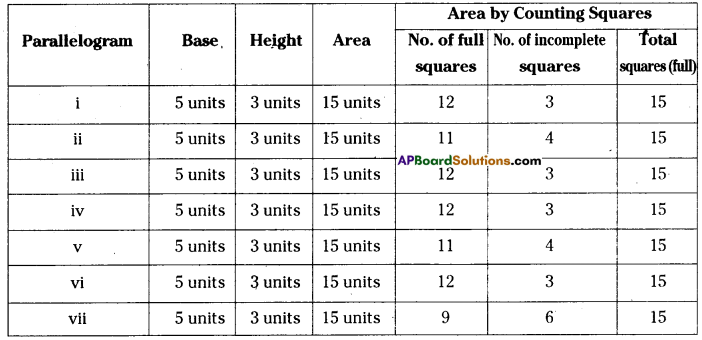
(ii) Do all parallelograms with equal base and equal heights have the same area ?
Solution:
Yes
![]()
Try This
Question
i) Why is the formula for finding the area of a rectangle related to the formula for finding the area of a parallelogram ? (Page No. 249)
Solution:
Any parallelogram can be modelled into a rectangle and hence, area of a parallelogram is related to the area of a rectangle.
ii) Explain why a rectangle is a parallelogram but a parallelogram may not be a rectangle.
Solution:
In a rectangle both pairs of opposite sides are parallel and hence it is a parallelogram. But each angle of a parallelogram is not always a right angle and hence it may not be a rectangle.
![]()
Try This
Question 1.
In the figure all triangles are on the base AB = 24 cm. Is the height of each of the triangles drawn on base AB, the same ? Will all the triangles have equal area ? Give reasons to support your answer. Are the triangles congruent also ? (Page No. 252)
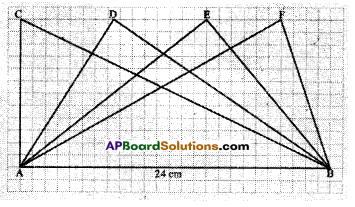
Solution:
Heights of all triangles are equal, as the triangles are drawn between same parallels.
Areas of all triangles are equal, as all the triangles can be modelled as half of same parallelo¬gram. But triangles are not congruent.