AP State Syllabus AP Board 7th Class Maths Solutions Chapter 12 Quadrilaterals Ex 2 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 12th Lesson Quadrilaterals Exercise 2
![]()
Question 1.
State whether true or false
(i) All rectangles are squares ( )
(ii) All rhombuses are parallelogram ( )
(iii) All squares arc rhombuses and also rectangles ( )
(iv) All squares are not parallelograms ( )
(v) All kites arc rhombuses ( )
(vi) All rhombuses are kites ( )
(vii) All parallelograms are trapeziums ( )
(viii) All squares are trapeziums ( )
Solution:
(i) All rectangles are squares ( False)
(ii) All rhombuses are parallelogram ( True)
(iii) All squares arc rhombuses and also rectangles ( True)
(iv) All squares are not parallelograms (False )
(v) All kites arc rhombuses ( False)
(vi) All rhombuses are kites (True )
(vii) All parallelograms are trapeziums ( True)
(viii) All squares are trapeziums ( True)
Question 2.
Explain how a square is a
(i) quadrilateral
(ii) parallelogram
(iii) rhombus
(iv) rectangle.
Solution:
i) quadrilateral : A square is a closed figure bounded by four line segments and hence it is a
quadrilateral.
ii) Parallelogram : In a square both pairs of opposite sides are parallel and hence it is a parallelogram.
iii) Rhombus : All four sides of a square are equal, thus it is a Rhombus.
iv) Rectangle : In a square each angle ¡s a right angle and hence it is a rectangle.
Question 3.
In a rhombus ABCD, ∠CBA = 40°.
Find the other angles.
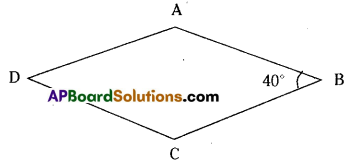
Given that ∠CBA , ∠B = 40°
We know that rhombus is a parallelogram and
adjacent angles are supplementary.
Thus ∠A + ∠B = 180°
∠A + 40° = 180°
∠A = 180° – 40° = 140°
Also opposite angles are equal.
∴ ∠A =∠C = 140°
∠D = ∠B = 40°
![]()
Question 4.
The adjacent angels of a parallelogram arex° and (2x + 30)°.
Find all the angles of the parallelogram.
Solution:

Given that the adjacent angles of a parallelogram are x° ; (2x + 30)°
Adjacent angles of a parallelogram are supplementary.
∴ x + (2x + 30) = 180°
3x + 30 = 180°
3x = 180° – 30° = 150°
x = \(\frac{150^{\circ}}{3}\) = 50°
∴ The adjacent angles are x = 50°
2x + 30°= 2 x 50 + 30 = 130°
∴ The other two angles are 50°, 130°
∴ The four angles are 50°, 130°, 50°, 130°
Question 5.
Explain how DEAR is a trapezium. Which of its two sides are parallel?
Solution:
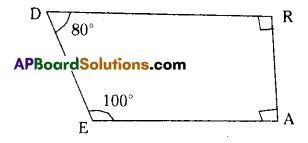
In quadrilateral DEAR
∠D = 80° and ∠E = 100°
Also ∠D + ∠E = 80°+ 100° = 180°
(∵ D, E are interior angles on the same side of \(\overline{\mathrm{DE}}\))
∴ DR //EA
Also ∠A = ∠R = 90° and ∠A + ∠R = 180°
∴ DEAR is a trapezium.
![]()
Question 6.
BASE is a rectangle. Its diagonals intersect atO. Findx, if OB = 5x+1 and OE = 2x + 4.
Solution:
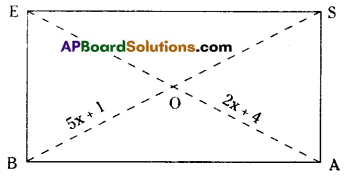
Given BASE is a rectangle.
OB = 5x + 1 and OA = 2x + 4
In a rectangle diagonals are equal.
BS = EA
(i.e.) 2 x BO = 2 x OA
2(5x + 1) = 2(2x + 4 )
10x + 2 = 4x + 8
10x – 4x = 8 – 2
6x = 6
x = 1
Question 7.
Is quadrilateral ABCD a parallelogram, if ∠A = 70° and ∠C = 65° ? Give reason.
Solution:
Given that in quadrilateral ABCD, ∠A = 70° and ∠C = 65°
∠A and ∠C are opposite angles and are not equal.
Hence quadrilateral ABCD is not a parallelogram.
![]()
Question 8.
Two adjacent sides of a parallelogram are in the ratio 5:3 the perimeter of the parallelogram is 48cm. Find the length of each of its sides.
Solution:
Given that the ratio of two adjacent sides of a parallelogram = 5 : 3
Sum of the terms of the ratio = 5 + 3 = 8
Sum of two sides = half of the perimeter = \(\frac { 1 }{ 2 }\) x 48 = 24 cm
∴ one side = \(\frac { 5 }{ 8 }\) x 24 = 15 cm
other side = \(\frac { 3 }{ 8 }\) x 24 = 9 cm
∴ The four sides are 15 cm, 9 cm, 15 cm, 9 cm ( opposite sides are equal)
Question 9.
The diagonals of the quadrilateral are perpendicular to each other. Is such a quadrilateral
always a rhombus? Draw a rough figure to justify your answer.
Solution:
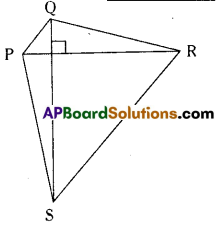
Given : Diagonals are perpendicular.
If the diagonals are perpendicular then the
quadrilateral need not necessarily be a rhombus.
Look at the figure,
the diagonals are perpendicular to each other.
But all the sides are not equal.
PR ⊥ QS but PQ ≠ QR ≠ RS ≠ SP
![]()
Question 10.
ABCD is a trapezium in which \(\overline{\mathrm{AB}} \| \overline{\mathrm{DC}}\) If ∠A = ∠B =30°, what are the measures of the other two angles?
Solution:

Given : ABCD is a trapezium.
∠A = ∠B = 30°
Since AB//CD,
∠A + ∠D = ∠B + ∠C = 180° (interior angles on the same side of a
transversal are supplementary)
30° + ∠D = 180°
∠D = 180° – 300°
= 150°
and 30° + ∠C = 180°
∠C = 180° – 30’
= 150°
![]()
Question 11.
Fill in the blanks.
(i) A parallelogram in which two adjacent sides are equal is a ………………….
(ii) A parallelogram in which one angle is 90° and two adjacent sides are equal is a ………………….
(iii) IntrapeziurnABCD,\(\overline{\mathrm{AB}} \| \overline{\mathrm{DC}}\) . If ∠D = x° then ∠A = ………………
(iv) Every diagonal in a parallelogram divides it into …………………. triangles.
(v) In parallelogram ABCD, its diagonals \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{BD}}\) intersect atO. IfAO = 5cm then AC = …………….. cm.
(vi) In a rhombus ABCD, its diagonals intersect at ‘O’. Then ∠AOB = …………. degrees.
(vii) ABCD is a parallelogram then ∠A — ∠C = ………………… degrees.
(viii) In a rectangle ABCD, the diagonal AC =10cm then the diagonal BD = …………… cm.
(ix) In a square ABCD, the diagonal \(\overline{\mathrm{AC}}\) is drawn. Then ∠BAC = …………
Solution:
(i) A parallelogram in which two adjacent sides are equal is a rhombus
(ii) A parallelogram in which one angle is 90° and two adjacent sides are equal is a square
(iii) IntrapeziurnABCD,\(\overline{\mathrm{AB}} \| \overline{\mathrm{DC}}\) . If ∠D = x° then ∠A = 180° – x
(iv) Every diagonal in a parallelogram divides it into two congruent triangles.
(v) In parallelogram ABCD, its diagonals \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{BD}}\) intersect atO. If AO = 5cm then AC = 10 cm.
(vi) In a rhombus ABCD, its diagonals intersect at ‘O’. Then ∠AOB = 90°
(vii) ABCD is a parallelogram then ∠A — ∠C = zero degrees.
(viii) In a rectangle ABCD, the diagonal AC =10cm then the diagonal BD = 10 cm.
(ix) In a square ABCD, the diagonal \(\overline{\mathrm{AC}}\) is drawn. Then ∠BAC = 45°