AP State Syllabus AP Board 7th Class Maths Solutions Chapter 12 Quadrilaterals Ex 1 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 12th Lesson Quadrilaterals Exercise 1
![]()
Question 1.
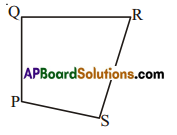
In quadrilateral PQRS
(i) Name the sides, angles, vertices and diagonals.
(ii) Also name all the pairs of adjacent sides, adjacent angles, opposite sides and opposite angles. .
Solution:
ï) In quadrilateral PQRS,
sides = PQ, QR, RS and SP
angles = ∠P, ∠Q, ∠R, and ∠S
vertices = P, Q, R and S
diagonals = PR and QS
ii) Pairs of adjacent sides = (PQ, QR), (QR. RS), (RS, SP), (SP, PQ)
Pairs of adjacent angles (∠P, ∠Q). (∠Q, ∠R), (∠R, ∠S), (∠S, ∠P)
Pairs of opposite sides = (PQ, RS) and (QR, PS)
Pairs of opposite angles = (∠P,∠R) and (∠Q, ∠S)
![]()
Question 2.
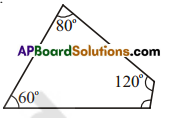
The three angles of a quadrilateral are 60°, 80° and 1200. Find the fourth angle?
Solution:
Given three angles = 60°,80°,120°
Sum of the given three angles = 60°+ 80° + 120° = 260°
Sum of the four Interior angles of a quadrilateral = 360°
∴ The fourth angle = 360° — 260° = 100°
Question 3.
The angles of a quadrilateral are in the ratio 2 : 3 : 4: 6. Find the measure of each of the four angles.
Solution:
Given that ratio of the four angles = 2 : 3 : 4 : 6
Sum of the terms in the ratio = 2 + 3 + 4 + 6 = 15
Sum of the four angles = 360°
∴ 1st angle = \(\frac { 2 }{ 15 }\) x 360° = 48°
2nd angle = \(\frac { 3 }{ 15 }\) x 360° = 72°
3rd angle = \(\frac { 4 }{ 15 }\) x 360° = 96°
4th angle = \(\frac { 6 }{ 15 }\) x 360° = 144°
Question 4.
The four angles of a quadrilateral are equal. Draw this quadrilateral in your notebook.
Find each of them.
Solution:

Sum of the four angles in a quadrilateral = 360°
Each of the angle = \(\frac{360^{\circ}}{4}\) = 90°
∠A = ∠B = ∠C = ∠D = 90°
![]()
Question 5.
In a quadrilateral, the angles arex°, (x + l0)°, (i+ 20)°, (x + 30)°. Find the angles.
Solution:
Given angles are x°, (x + 10)°, (x + 20)°, (x + 30)°
Sum of the four angles = x + x + 10° + x + 20° + x + 30° = 4x + 60°
But the sum of the four angles = 360°
4 x 60° = 60° = 360°
4x = 360° – 60° = 300°
x = \(\frac{300^{\circ}}{4}\) = 75°
∴ The angles are x = 750
x + 10°- 75°+ 10° = 85°
x + 20° = 75° +20° = 95°
x + 30° = 75° + 30° = 105°
![]()
Question 6.
The angles of a quadrilateral cannot be in the ratio 1: 2 : 3 : 6. Why? Give reasons.
(Hint: Try to draw a rough diagram of this quadrilateral)
Solution:
Given that the angles of a quadrilateral cant be in the ratio 1: 2 : 3 : 6
If the ratio is 1 : 2 : 3 : 6 then
the sum of terms of ratio = I + 2 + 3 + 6 = 12
Sum of the angles = 360°
∴ 1st angle = \(\frac{1}{12}\) x 360° = 30°
2nd angle = \(\frac{2}{12}\)x 360° = 60°
3rd angle = \(\frac{3}{12}\) x 360° = 90°
4th angle = \(\frac{3}{12}\) x 360° = I80
i.e., 4th angle is 180°, a straight angle.
A quadrIlateral cant he formed with these angles.