AP State Syllabus AP Board 7th Class Maths Solutions Chapter 11 Exponents Ex 1 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 11th Lesson Exponents Exercise 1
![]()
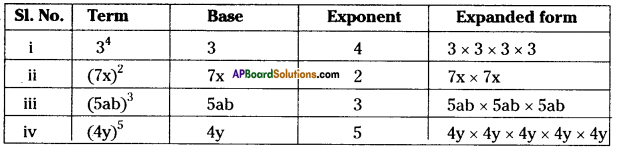
Question 1.
Write the base and the exponent in each case. Also, write the term in the expanded form.
(i) 34
(ii) (7x)2
(iii) (5ab)3
(iv) (4y)5
Solution:
Question 2.
Write the exponential form of each expression.
(i) 7 × 7 × 7 × 7 × 7
(ii) 3 × 3 × 3 × 5 × 5 × 5 × 5
(iii) 2 × 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5 × 5
Solution:
(i) 7 × 7 × 7 × 7 × 7 = 75
(ii) 3 × 3 × 3 × 5 × 5 × 5 × 5 = 33 × 54
(iii) 2 × 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5 × 5 = 23 × 34 × 53
![]()
Question 3.
Express the following as the product of exponents through prime factorization.
(i) 288
(ii) 1250
(iii) 2250
(iv) 3600
(v) 2400
Solution:
(i) 288
1) 288 = 2 × 144
= 2 × 2 × 72
= 2 × 2 × 2 × 36
= 2 × 2 × 2 × 2 × 18
= 2 × 2 × 2 × 2 × 2 × 9
= (2 × 2 × 2 × 2× 2) × (3 × 3)
= 25 × 32

![]()
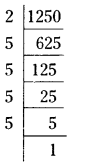
(ii) 1250 = 2 × 625
= 2 × 5 × 125
= 2 × 5 × 5 × 25
= 2 × 5 × 5 × 5 × 5
= 2 × 54
(iii) 2250 = 2 × 1125
= 2 × 3 × 375
= 2 × 3 × 3 × 125
= 2 × 3 × 3 × 5 × 25
= 2 × 3 × 3 × 5 × 5 × 5
= 21 × 32 × 53

![]()
(iv) 3600 = 2 × 1800
= 2 × 2 × 900
=2 × 2 × 2 × 450
=2 × 2 × 2 × 2 × 225
= ( 2 × 2 × 2 × 2 ) × 3 × 75
= (2 × 2 × 2 × 2) × (3 × 3) × 25
= (2 × 2 × 2 × 2) × (3 × 3) × (5 × 5)
= 24 × 32 × 52

![]()
(v) 2400
2400 = 2 × 1200
= 2 × 2 × 600
= 2 × 2 × 2 × 300
= 2 × 2 × 2 × 2 × 150
= 2 × 2 × 2 × 2 × 2 × 75
= (2 × 2 × 2 × 2 × 2) × 3 × 25
= (2 × 2 × 2 × 2 × 2) × 3 × (5 × 5)
= 25 × 31

Question 4.
Identify the greater number in each of the following pairs.
(i) 23 or 32
(ii) 53 or 35
(iii) 28 or 82
Solution:
(i) 23 or 32 = 23 = 2 × 2 × 2 = 8 and 32 = 3 × 3 = 9
∴ 23 < 32 or 32 > 23
(ii) 53 or 35 = 53 = 5 × 5 × 5 = 125 and 35 = 3 × 3 × 3 × 3 × 3 = 243
∴ 35 > 53
![]()
(iii) 28 or 82 = 28 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
82 = 8 × 8 = 64
∴ 28 > 82
Question 5.
If a = 3, b = 2 find the value of
(i) ab + ba
(ii) aa + bb
(iii) (a + b)ab
(iv)(a – b)a
Solution:
(i) ab + ba = 32 + 23 = 3 × 3 + 2 × 2 × 2 = 9 + 8 =17
(ii) aa + bb = 33 + 22 = 3 × 3 × 3 + 2 × 2 = 27 + 4 = 31
(iii) (a + b)b = (3 + 2)2 = 52 = 5 × 5 = 25
(iv)(a – b)a = (3 – 2)2= 12 = 1 × 1 = 1 .